Category theory
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (November 2009) |
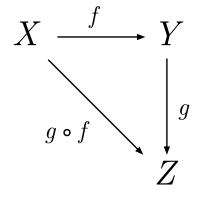
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory is used in almost all areas of mathematics. In particular, many constructions of new mathematical objects from previous ones that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient spaces, direct products, completion, and duality.
Many areas of computer science also rely on category theory, such as functional programming and semantics.
A
The second fundamental concept of category theory is the concept of a
Categories, objects, and morphisms
Categories
A category C consists of the following three mathematical entities:
- A class ob(C), whose elements are called objects;
- A class hom(C), whose elements are called morphisms or maps or arrows.
Each morphism f has a source object a and target object b.
The expression f : a → b, would be verbally stated as "f is a morphism from a to b".
The expression hom(a, b) – alternatively expressed as homC(a, b), mor(a, b), or C(a, b) – denotes the hom-class of all morphisms from a to b. - A binary operation ∘, called composition of morphisms, such that
for any three objects a, b, and c, we have
- ∘ : hom(b, c) × hom(a, b) → hom(a, c).
- The composition of f : a → b and g : b → c is written as g ∘ f or gf,[a] governed by two axioms:
- 1. Associativity: If f : a → b, g : b → c, and h : c → d then
- h ∘ (g ∘ f) = (h ∘ g) ∘ f
- 2. identity morphismfor x,
such that- for every morphism f : a → b, we have
- 1b ∘ f = f = f ∘ 1a
- From the axioms, it can be proved that there is exactly one identity morphismfor every object.
- 1.
Morphisms
Relations among morphisms (such as fg = h) are often depicted using commutative diagrams, with "points" (corners) representing objects and "arrows" representing morphisms.
Morphisms can have any of the following properties. A morphism f : a → b is a:
- monomorphism (or monic) if f ∘ g1 = f ∘ g2 implies g1 = g2 for all morphisms g1, g2 : x → a.
- epimorphism (or epic) if g1 ∘ f = g2 ∘ f implies g1 = g2 for all morphisms g1, g2 : b → x.
- bimorphism if f is both epic and monic.
- isomorphism if there exists a morphism g : b → a such that f ∘ g = 1b and g ∘ f = 1a.[b]
- endomorphism if a = b. end(a) denotes the class of endomorphisms of a.
- automorphism if f is both an endomorphism and an isomorphism. aut(a) denotes the class of automorphisms of a.
- retractionif a right inverse of f exists, i.e. if there exists a morphism g : b → a with f ∘ g = 1b.
- section if a left inverse of f exists, i.e. if there exists a morphism g : b → a with g ∘ f = 1a.
Every retraction is an epimorphism, and every section is a monomorphism. Furthermore, the following three statements are equivalent:
- f is a monomorphism and a retraction;
- f is an epimorphism and a section;
- f is an isomorphism.
Functors
Functors are structure-preserving maps between categories. They can be thought of as morphisms in the category of all (small) categories.
A (covariant) functor F from a category C to a category D, written F : C → D, consists of:
- for each object x in C, an object F(x) in D; and
- for each morphism f : x → y in C, a morphism F(f) : F(x) → F(y) in D,
such that the following two properties hold:
- For every object x in C, F(1x) = 1F(x);
- For all morphisms f : x → y and g : y → z, F(g ∘ f) = F(g) ∘ F(f).
A contravariant functor F: C → D is like a covariant functor, except that it "turns morphisms around" ("reverses all the arrows"). More specifically, every morphism f : x → y in C must be assigned to a morphism F(f) : F(y) → F(x) in D. In other words, a contravariant functor acts as a covariant functor from the opposite category Cop to D.
Natural transformations
A natural transformation is a relation between two functors. Functors often describe "natural constructions" and natural transformations then describe "natural homomorphisms" between two such constructions. Sometimes two quite different constructions yield "the same" result; this is expressed by a natural isomorphism between the two functors.
If F and G are (covariant) functors between the categories C and D, then a natural transformation η from F to G associates to every object X in C a morphism ηX : F(X) → G(X) in D such that for every morphism f : X → Y in C, we have ηY ∘ F(f) = G(f) ∘ ηX; this means that the following diagram is commutative:

The two functors F and G are called naturally isomorphic if there exists a natural transformation from F to G such that ηX is an isomorphism for every object X in C.
Other concepts
Universal constructions, limits, and colimits
Using the language of category theory, many areas of mathematical study can be categorized. Categories include sets, groups and topologies.
Each category is distinguished by properties that all its objects have in common, such as the empty set or the product of two topologies, yet in the definition of a category, objects are considered atomic, i.e., we do not know whether an object A is a set, a topology, or any other abstract concept. Hence, the challenge is to define special objects without referring to the internal structure of those objects. To define the empty set without referring to elements, or the product topology without referring to open sets, one can characterize these objects in terms of their relations to other objects, as given by the morphisms of the respective categories. Thus, the task is to find universal properties that uniquely determine the objects of interest.
Numerous important constructions can be described in a purely categorical way if the category limit can be developed and dualized to yield the notion of a colimit.
Equivalent categories
It is a natural question to ask: under which conditions can two categories be considered essentially the same, in the sense that theorems about one category can readily be transformed into theorems about the other category? The major tool one employs to describe such a situation is called equivalence of categories, which is given by appropriate functors between two categories. Categorical equivalence has found numerous applications in mathematics.
Further concepts and results
The definitions of categories and functors provide only the very basics of categorical algebra; additional important topics are listed below. Although there are strong interrelations between all of these topics, the given order can be considered as a guideline for further reading.
- The functor category DC has as objects the functors from C to D and as morphisms the natural transformations of such functors. The Yoneda lemma is one of the most famous basic results of category theory; it describes representable functors in functor categories.
- Duality: Every statement, theorem, or definition in category theory has a dual which is essentially obtained by "reversing all the arrows". If one statement is true in a category C then its dual is true in the dual category Cop. This duality, which is transparent at the level of category theory, is often obscured in applications and can lead to surprising relationships.
- Adjoint functors: A functor can be left (or right) adjoint to another functor that maps in the opposite direction. Such a pair of adjoint functors typically arises from a construction defined by a universal property; this can be seen as a more abstract and powerful view on universal properties.
Higher-dimensional categories
Many of the above concepts, especially equivalence of categories, adjoint functor pairs, and functor categories, can be situated into the context of higher-dimensional categories. Briefly, if we consider a morphism between two objects as a "process taking us from one object to another", then higher-dimensional categories allow us to profitably generalize this by considering "higher-dimensional processes".
For example, a (strict)
This process can be extended for all
Higher-dimensional categories are part of the broader mathematical field of higher-dimensional algebra, a concept introduced by Ronald Brown. For a conversational introduction to these ideas, see John Baez, 'A Tale of n-categories' (1996).
Historical notes
This section needs additional citations for verification. (November 2015) |
It should be observed first that the whole concept of a category is essentially an auxiliary one; our basic concepts are essentially those of a functor and of a natural transformation [...]
Whilst specific examples of functors and natural transformations had been given by Samuel Eilenberg and Saunders Mac Lane in a 1942 paper on group theory,[2] these concepts were introduced in a more general sense, together with the additional notion of categories, in a 1945 paper by the same authors[1] (who discussed applications of category theory to the field of algebraic topology).[3] Their work was an important part of the transition from intuitive and geometric homology to homological algebra, Eilenberg and Mac Lane later writing that their goal was to understand natural transformations, which first required the definition of functors, then categories.
Category theory was originally introduced for the need of
Certain categories called
Categorical logic is now a well-defined field based on type theory for intuitionistic logics, with applications in functional programming and domain theory, where a cartesian closed category is taken as a non-syntactic description of a lambda calculus. At the very least, category theoretic language clarifies what exactly these related areas have in common (in some abstract sense).
Category theory has been applied in other fields as well, see
More recent efforts to introduce undergraduates to categories as a foundation for mathematics include those of William Lawvere and Rosebrugh (2003) and Lawvere and Stephen Schanuel (1997) and Mirroslav Yotov (2012).
See also
Notes
- ^ Some authors compose in the opposite order, writing fg or f ∘ g for g ∘ f. Computer scientists using category theory very commonly write f ; g for g ∘ f
- ^ A morphism that is both epic and monic is not necessarily an isomorphism. An elementary counterexample: in the category consisting of two objects A and B, the identity morphisms, and a single morphism f from A to B, f is both epic and monic but is not an isomorphism.
References
Citations
- ^ (PDF) from the original on 2022-10-10.
- .
- ^ Marquis, Jean-Pierre (2019). "Category Theory". Stanford Encyclopedia of Philosophy. Department of Philosophy, Stanford University. Retrieved 26 September 2022.
- ISBN 9780190641221.
- S2CID 115169297.
Sources
- Adámek, Jiří; Herrlich, Horst; Strecker, George E. (2004). Abstract and Concrete Categories. Heldermann Verlag Berlin.
- Awodey, Steve (2010). Category Theory. Oxford University Press. ISBN 978-0199237180.
- Barr, Michael; Wells, Charles (2012) [1995], Category Theory for Computing Science, Reprints in Theory and Applications of Categories, vol. 22 (3rd ed.).
- MR 2178101.
- Borceux, Francis (1994). Handbook of categorical algebra. Encyclopedia of Mathematics and its Applications. Cambridge University Press. pp. 50–52. ISBN 9780521441780.
- Freyd, Peter J. (2003) [1964]. Abelian Categories. Reprints in Theory and Applications of Categories. Vol. 3.
- ISBN 978-0-08-088701-2.
- ISBN 978-0-486-45026-1.
- ISBN 978-3-88538-001-6..
- ISBN 978-3-540-27949-5.
- ISBN 978-0-521-01060-3.
- Lawvere, F. William; ISBN 978-0-521-89485-2.
- ISBN 978-0-521-53215-0. Archived from the originalon 2003-10-25. Retrieved 2006-04-03.
- ISBN 9781107044241.
- MR 2522659.
- MR 1712872.
- ISBN 978-0-8218-1646-2.
- Martini, A.; Ehrig, H.; Nunes, D. (1996). "Elements of basic category theory". Technical Report. 96 (5).
- ISBN 978-3-7643-5731-3.
- Pedicchio, Maria Cristina; Tholen, Walter, eds. (2004). Categorical foundations. Special topics in order, topology, algebra, and sheaf theory. Encyclopedia of Mathematics and Its Applications. Vol. 97. Zbl 1034.18001.
- ISBN 978-0-262-66071-6.
- Schalk, A.; Simmons, H. (2005). An introduction to Category Theory in four easy movements (PDF). Archived from the original (PDF) on 2017-03-21. Retrieved 2007-12-03. Notes for a course offered as part of the MSc. in Manchester University.
- Simmons, Harold (2011), An Introduction to Category Theory, ISBN 978-0521283045.
- Bibcode:2010arXiv1001.4071S., draft of a book.
- Taylor, Paul (1999). Practical Foundations of Mathematics. Cambridge Studies in Advanced Mathematics. Vol. 59. Cambridge University Press. ISBN 978-0-521-63107-5.
- Turi, Daniele (1996–2001). "Category Theory Lecture Notes" (PDF). Retrieved 11 December 2009. Based on Mac Lane 1998.
Further reading
- Marquis, Jean-Pierre (2008). From a Geometrical Point of View: A Study of the History and Philosophy of Category Theory. Springer. ISBN 978-1-4020-9384-5.
External links
- Theory and Application of Categories, an electronic journal of category theory, full text, free, since 1995.
- nLab, a wiki project on mathematics, physics and philosophy with emphasis on the n-categorical point of view.
- The n-Category Café, essentially a colloquium on topics in category theory.
- Category Theory, a web page of links to lecture notes and freely available books on category theory.
- Hillman, Chris (2001), A Categorical Primer, CiteSeerX 10.1.1.24.3264, a formal introduction to category theory.
- Adamek, J.; Herrlich, H.; Stecker, G. "Abstract and Concrete Categories-The Joy of Cats" (PDF). Archived (PDF) from the original on 2006-06-10.
- "Category Theory" entry by Jean-Pierre Marquis in the Stanford Encyclopedia of Philosophy, with an extensive bibliography.
- List of academic conferences on category theory
- Baez, John (1996). "The Tale of n-categories". — An informal introduction to higher order categories.
- WildCats is a category theory package for universal properties.
- The catsters's channel on YouTube, a channel about category theory.
- Category theory at PlanetMath..
- Video archive of recorded talks relevant to categories, logic and the foundations of physics.
- Interactive Web page which generates examples of categorical constructions in the category of finite sets.
- Category Theory for the Sciences, an instruction on category theory as a tool throughout the sciences.
- Category Theory for Programmers A book in blog form explaining category theory for computer programmers.
- Introduction to category theory.

