Search results
Did you mean: parable
The page "File:Parabola" does not exist. You can ask for it to be uploaded, but consider checking the search results below to see whether the topic is already covered.
- English Spanish Curva dual de la parábola. Si el centro del círculo esta sobre la parábola su dual es otra parábola. URL: https://commons.wikimedia.org/wiki/user:Rectas...(1,000 × 1,000 (383 KB)) - 15:35, 16 February 2022
- English Parabola with focus and directrix described at URL: https://en.wikipedia.org/wiki/File:Parabola_with_focus_and_directrix.jpg determination method...(506 × 394 (24 KB)) - 08:20, 26 May 2025
- image is a derivative work of the following images: File:Partes_de_una_parábola.svg licensed with Cc-by-sa-3.0-migrated, GFDL 2008-06-05T21:27:06Z Magister...(409 × 303 (19 KB)) - 09:14, 28 October 2020
- Image:Parabola-and-inscribed_triangle.png licensed with PD-user 2007-08-16T18:25:02Z Jeff G. 243x266 (9780 Bytes) Replaced from Image:Parabola and inscribed...(243 × 200 (3 KB)) - 22:59, 23 April 2021
- the following license: English Spanish Dual de la parábola. Centro del círculo en el foco de la parábola. URL: https://commons.wikimedia.org/wiki/user:Rectas...(1,000 × 1,000 (375 KB)) - 15:39, 16 February 2022
- the following license: English Red and yellow Parabola GNU/Linux-libre logo operating system: Parabola GNU/Linux-libre sRGB color hex triplet: FFE119...(1,000 × 1,000 (4 KB)) - 22:46, 3 May 2025
- Parabola GNU/Linux-libre - Official Wallpaper - Landscape Parabola GNU/Linux-libre Wiki Parabola GNU/Linux-libre - Official Wallpaper - Landscape This...(1,366 × 768 (1.39 MB)) - 23:06, 1 July 2025
- of this work, hereby publish it under the following license: English A parabola is the locus of all points equally distant between a point and line. author...(1,311 × 623 (44 KB)) - 16:14, 29 July 2024
- holder of this work, hereby publish it under the following license: English Parabola Russian Парабола Arabic قطع مكافئ Japanese 放物線 . author name string: Matsievsky...(388 × 289 (6 KB)) - 00:39, 20 January 2024
- wikipedia. The cissoid of Diocles can be produced by rolling a parabola around another parabola, and tracing the roulette of its vertex. This image was made...(500 × 309 (12 KB)) - 13:23, 17 October 2024
- publish it under the following license: English Spanish La curva dual de la parábola respecto a un círculo interior es una elipse. URL: https://commons.wikimedia...(1,000 × 1,000 (450 KB)) - 15:35, 16 February 2022
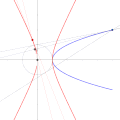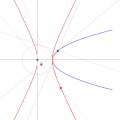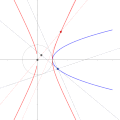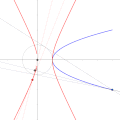
- publish it under the following license: English Spanish La dual de la parábola respecto a un círculo exterior es una hipérbola. URL: https://commons.wikimedia...(1,000 × 1,000 (446 KB)) - 15:35, 16 February 2022
- following license: English For a given focus and directrix, they determine the parabola with points equally distant from focus and from directrix. author name...(928 × 622 (43 KB)) - 23:35, 22 March 2024
- Attribution-Share Alike 3.0 truetrue English Parts of a parabola. Tagalog Bahagi ng parabola. author name string: Maninipnay Wikimedia username: Maninipnay...(450 × 368 (10 KB)) - 06:32, 12 June 2025
- holder of this work, hereby publish it under the following license: English Parabola at the Geometer's Sketchpad Literary Chinese 畢弗於幾何畫板 URL: https://commons...(1,440 × 868 (56 KB)) - 01:36, 26 September 2022
- names refer to cs.wikipedia. 2006-03-04 00:21 D1ce 118×123× (1468 bytes) Parabola v kartézském souřadnicovém systému rozvírající se do kladné části osy y...(118 × 123 (1 KB)) - 14:59, 26 October 2024
- names refer to cs.wikipedia. 2006-03-04 00:18 D1ce 118×123× (1463 bytes) Parabola v kartézském souřadnicovém systému rozvírající se do kladné části osy x...(118 × 123 (1 KB)) - 14:56, 26 October 2024
- names refer to cs.wikipedia. 2006-03-04 00:23 D1ce 118×123× (1378 bytes) Parabola v kartézském souřadnicovém systému rozvírající se do kladné části osy x...(118 × 123 (1 KB)) - 13:36, 26 October 2024
- BY 4.0 Creative Commons Attribution 4.0 truetrue English SNG TV-Osaka Parabola Antenna at Tenjin Matsuri Festival 2025 Japanese テレビ大阪の中継車に設置されているパラボラアンテナ(2025年天神祭り・大川)...(4,320 × 3,240 (2.78 MB)) - 00:26, 26 July 2025
- version of image on Commons at [http://commons.wikimedia.org/wiki/Image:Parabola-and-inscribed_triangle.png] == {{int:license}} == {{PD-user|Jim.belk}}...(243 × 266 (13 KB)) - 10:28, 17 August 2024
- DescriptionWag-131-3 Parabola Envelope.png English: Figure - Parabola Envelope. Date 1911 Source Elements of the Differential and Integral Calculus (revised)