Fractal

In

One way that fractals are different from finite

Starting in the 17th century with notions of recursion, fractals have moved through increasingly rigorous mathematical treatment to the study of continuous but not differentiable functions in the 19th century by the seminal work of Bernard Bolzano, Bernhard Riemann, and Karl Weierstrass,^[7] and on to the coining of the word fractal in the 20th century with a subsequent burgeoning of interest in fractals and computer-based modelling in the 20th century.^[8][9]

There is some disagreement among mathematicians about how the concept of a fractal should be formally defined. Mandelbrot himself summarized it as "beautiful, damn hard, increasingly useful. That's fractals."

The consensus among mathematicians is that theoretical fractals are infinitely self-similar iterated and detailed mathematical constructs, of which many examples have been formulated and studied.^[1][2][3] Fractals are not limited to geometric patterns, but can also describe processes in time.^{[5][4][13][14][15][16]} Fractal patterns with various degrees of self-similarity have been rendered or studied in visual, physical, and aural media^[17] and found in nature,^{[18][19][20][21]} technology,^{[22][23][24][25]} art,^[26][27] and architecture.^[28] Fractals are of particular relevance in the field of chaos theory because they show up in the geometric depictions of most chaotic processes (typically either as attractors or as boundaries between basins of attraction).^[29]

Etymology

The term "fractal" was coined by the mathematician

The word "fractal" often has different connotations for the lay public as opposed to mathematicians, where the public is more likely to be familiar with fractal art than the mathematical concept. The mathematical concept is difficult to define formally, even for mathematicians, but key features can be understood with a little mathematical background.

The feature of "self-similarity", for instance, is easily understood by analogy to zooming in with a lens or other device that zooms in on digital images to uncover finer, previously invisible, new structure. If this is done on fractals, however, no new detail appears; nothing changes and the same pattern repeats over and over, or for some fractals, nearly the same pattern reappears over and over. Self-similarity itself is not necessarily counter-intuitive (e.g., people have pondered self-similarity informally such as in the infinite regress in parallel mirrors or the homunculus, the little man inside the head of the little man inside the head ...). The difference for fractals is that the pattern reproduced must be detailed.^{[1]: 166, 18 [2][31]}

This idea of being detailed relates to another feature that can be understood without much mathematical background: Having a

This also leads to understanding a third feature, that fractals as mathematical equations are "nowhere

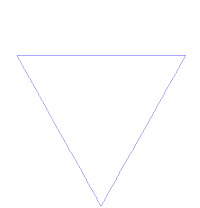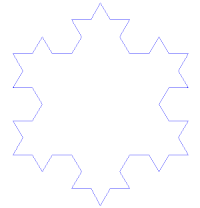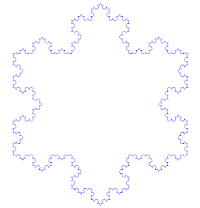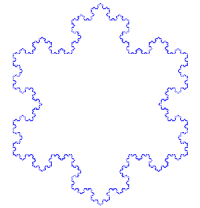
The history of fractals traces a path from chiefly theoretical studies to modern applications in computer graphics, with several notable people contributing canonical fractal forms along the way.^[8][9] A common theme in traditional African architecture is the use of fractal scaling, whereby small parts of the structure tend to look similar to larger parts, such as a circular village made of circular houses.^[34] According to

In addition, the quotient difference becomes arbitrarily large as the summation index increases.[36] Not long after that, in 1883, Georg Cantor, who attended lectures by Weierstrass,^[9] published examples of subsets of the real line known as Cantor sets, which had unusual properties and are now recognized as fractals.^{[8]: 11–24} Also in the last part of that century, Felix Klein and Henri Poincaré introduced a category of fractal that has come to be called "self-inverse" fractals.^[1]: 166

One of the next milestones came in 1904, when

Very shortly after that work was submitted, by March 1918, Felix Hausdorff expanded the definition of "dimension", significantly for the evolution of the definition of fractals, to allow for sets to have non-integer dimensions.^[9] The idea of self-similar curves was taken further by Paul Lévy, who, in his 1938 paper Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole, described a new fractal curve, the Lévy C curve.^{[notes 1]}

Different researchers have postulated that without the aid of modern computer graphics, early investigators were limited to what they could depict in manual drawings, so lacked the means to visualize the beauty and appreciate some of the implications of many of the patterns they had discovered (the Julia set, for instance, could only be visualized through a few iterations as very simple drawings).

In 1975,[31] Mandelbrot solidified hundreds of years of thought and mathematical development in coining the word "fractal" and illustrated his mathematical definition with striking computer-constructed visualizations. These images, such as of his canonical Mandelbrot set, captured the popular imagination; many of them were based on recursion, leading to the popular meaning of the term "fractal".^{[39][33][8][35]}

In 1980, Loren Carpenter gave a presentation at the SIGGRAPH where he introduced his software for generating and rendering fractally generated landscapes.^[40]

Definition and characteristics

One often cited description that Mandelbrot published to describe geometric fractals is "a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole";^[1] this is generally helpful but limited. Authors disagree on the exact definition of fractal, but most usually elaborate on the basic ideas of self-similarity and the unusual relationship fractals have with the space they are embedded in.^{[1][5][2][4][41]}

One point agreed on is that fractal patterns are characterized by

Because of the trouble involved in finding one definition for fractals, some argue that fractals should not be strictly defined at all. According to Falconer, fractals should be only generally characterized by a gestalt of the following features;^[2]

• Self-similarity, which may include:

• Exact self-similarity: identical at all scales, such as the Koch snowflake
• Quasi self-similarity: approximates the same pattern at different scales; may contain small copies of the entire fractal in distorted and degenerate forms; e.g., the Mandelbrot set's satellites are approximations of the entire set, but not exact copies.
• Statistical self-similarity: repeats a pattern
  coastline of Britain for which one would not expect to find a segment scaled and repeated as neatly as the repeated unit that defines fractals like the Koch snowflake.^[4]
• Qualitative self-similarity: as in a time series[13]
• Multifractal
  scaling: characterized by more than one fractal dimension or scaling rule

• Fine or detailed structure at arbitrarily small scales. A consequence of this structure is fractals may have
  emergent properties^[43]
  (related to the next criterion in this list).
• Irregularity locally and globally that cannot easily be described in the language of traditional Euclidean geometry other than as the limit of a recursively defined sequence of stages. For images of fractal patterns, this has been expressed by phrases such as "smoothly piling up surfaces" and "swirls upon swirls";^[6]see Common techniques for generating fractals.

As a group, these criteria form guidelines for excluding certain cases, such as those that may be self-similar without having other typically fractal features. A straight line, for instance, is self-similar but not fractal because it lacks detail, and is easily described in Euclidean language without a need for recursion.^[1][4]

Common techniques for generating fractals

Images of fractals can be created by fractal generating programs. Because of the butterfly effect, a small change in a single variable can have an unpredictable outcome.

• Sierpinski gasket, Peano curve, Harter-Heighway dragon curve, T-square, Menger sponge
• Strange attractors – use iterations of a map or solutions of a system of initial-value differential or difference equations that exhibit chaos (e.g., see multifractal image, or the logistic map
  )
• space-filling curves
  and tilings
• Escape-time fractals – use a
  Nova fractal and Lyapunov fractal
  . The 2d vector fields that are generated by one or two iterations of escape-time formulae also give rise to a fractal form when points (or pixel data) are passed through this field repeatedly.
• Random fractals – use stochastic rules; e.g.,
  fractal landscapes, trajectories of Brownian motion and the Brownian tree (i.e., dendritic fractals generated by modeling diffusion-limited aggregation or reaction-limited aggregation clusters).^[4]

alternating link

• Sierpinski carpet are examples of finite subdivision rules, as is barycentric subdivision
  .

Applications

Simulated fractals

Fractal patterns have been modeled extensively, albeit within a range of scales rather than infinitely, owing to the practical limits of physical time and space. Models may simulate theoretical fractals or natural phenomena with fractal features. The outputs of the modelling process may be highly artistic renderings, outputs for investigation, or benchmarks for fractal analysis. Some specific applications of fractals to technology are listed elsewhere. Images and other outputs of modelling are normally referred to as being "fractals" even if they do not have strictly fractal characteristics, such as when it is possible to zoom into a region of the fractal image that does not exhibit any fractal properties. Also, these may include calculation or display artifacts which are not characteristics of true fractals.

Modeled fractals may be sounds,^[17] digital images, electrochemical patterns, circadian rhythms,^[49] etc. Fractal patterns have been reconstructed in physical 3-dimensional space

L-systems techniques.^[21]

The recursive nature of some patterns is obvious in certain examples—a branch from a tree or a frond from a fern is a miniature replica of the whole: not identical, but similar in nature. Similarly, random fractals have been used to describe/create many highly irregular real-world objects, such as coastlines and mountains. A limitation of modeling fractals is that resemblance of a fractal model to a natural phenomenon does not prove that the phenomenon being modeled is formed by a process similar to the modeling algorithms.

Natural phenomena with fractal features

Further information: Patterns in nature

Approximate fractals found in nature display self-similarity over extended, but finite, scale ranges. The connection between fractals and leaves, for instance, is currently being used to determine how much carbon is contained in trees.^[50] Phenomena known to have fractal features include:

• Actin cytoskeleton^[51]
• Algae
• Animal coloration patterns
• pulmonary vessels^[46]
• Brownian motion (generated by a one-dimensional Wiener process).^[52]
• Clouds and rainfall areas^[53]
• Coastlines
• Craters
• Crystals^[54]
• DNA
• Dust grains^[55]
• Earthquakes^[25][56]
• Fault lines
• Geometrical optics[57]
• Heart rates^[18]
• Heart sounds
• Lake shorelines and areas^[58][59][60]
• Lightning bolts
• Mountain-goat horns
• Neurons
• Polymers
• Percolation
• Mountain ranges
• Ocean waves^[61]
• Pineapple
• Proteins^[62]
• Psychedelic Experience
• Purkinje cells^[63]
• Rings of Saturn^[64][65]
• River networks
• Romanesco broccoli
• Snowflakes^[66]
• Soil pores^[67]
• Surfaces in turbulent flows^[68][69]
• Trees

• 
  Frost crystals occurring naturally on cold glass form fractal patterns
• 
  Fractal basin boundary in a geometrical optical system^[57]
• 
  A fractal is formed when pulling apart two glue-covered

  acrylic

  sheets
• 
  High-voltage breakdown within a 4 in (100 mm) block of acrylic glass creates a fractal Lichtenberg figure
• 
  self-similar

  form approximating a natural fractal
• 
  Fractal defrosting patterns, polar Mars. The patterns are formed by sublimation of frozen CO₂. Width of image is about a kilometer.
• 
  Slime mold Brefeldia maxima growing fractally on wood
• 
  Psilomelane dendrites in the Solnhofen Limestone

Fractals in cell biology

Fractals often appear in the realm of living organisms where they arise through branching processes and other complex pattern formation. Ian Wong and co-workers have shown that migrating cells can form fractals by clustering and branching.^[70] Nerve cells function through processes at the cell surface, with phenomena that are enhanced by largely increasing the surface to volume ratio. As a consequence nerve cells often are found to form into fractal patterns.^[71] These processes are crucial in cell physiology and different pathologies.^[72]

Multiple subcellular structures also are found to assemble into fractals. Diego Krapf has shown that through branching processes the actin filaments in human cells assemble into fractal patterns.^[57] Similarly Matthias Weiss showed that the endoplasmic reticulum displays fractal features.^[73] The current understanding is that fractals are ubiquitous in cell biology, from proteins, to organelles, to whole cells.

In creative works

Further information: Fractal art and Mathematics and art

Since 1999 numerous scientific groups have performed fractal analysis on over 50 paintings created by Jackson Pollock by pouring paint directly onto horizontal canvasses.^{[74][75] [76]}

Recently, fractal analysis has been used to achieve a 93% success rate in distinguishing real from imitation Pollocks.^[77] Cognitive neuroscientists have shown that Pollock's fractals induce the same stress-reduction in observers as computer-generated fractals and Nature's fractals.^[78]

Decalcomania, a technique used by artists such as Max Ernst, can produce fractal-like patterns.^[79] It involves pressing paint between two surfaces and pulling them apart.

Cyberneticist Ron Eglash has suggested that fractal geometry and mathematics are prevalent in African art, games, divination, trade, and architecture. Circular houses appear in circles of circles, rectangular houses in rectangles of rectangles, and so on. Such scaling patterns can also be found in African textiles, sculpture, and even cornrow hairstyles.^[27][80] Hokky Situngkir also suggested the similar properties in Indonesian traditional art, batik, and ornaments found in traditional houses.^[81][82]

Ethnomathematician Ron Eglash has discussed the planned layout of

Benin city using fractals as the basis, not only in the city itself and the villages but even in the rooms of houses. He commented that "When Europeans first came to Africa, they considered the architecture very disorganised and thus primitive. It never occurred to them that the Africans might have been using a form of mathematics that they hadn't even discovered yet."^[83]

In a 1996 interview with

Sierpinski triangle (a.k.a. Sierpinski gasket), but that the edited novel is "more like a lopsided Sierpinsky Gasket".^[26]

Some works by the Dutch artist M. C. Escher, such as Circle Limit III, contain shapes repeated to infinity that become smaller and smaller as they get near to the edges, in a pattern that would always look the same if zoomed in.

Aesthetics and Psychological Effects of Fractal Based Design:^[84] Highly prevalent in nature, fractal patterns possess self-similar components that repeat at varying size scales. The perceptual experience of human-made environments can be impacted with inclusion of these natural patterns. Previous work has demonstrated consistent trends in preference for and complexity estimates of fractal patterns. However, limited information has been gathered on the impact of other visual judgments. Here we examine the aesthetic and perceptual experience of fractal ‘global-forest’ designs already installed in humanmade spaces and demonstrate how fractal pattern components are associated with positive psychological experiences that can be utilized to promote occupant well-being. These designs are composite fractal patterns consisting of individual fractal ‘tree-seeds’ which combine to create a ‘global fractal forest.’ The local ‘tree-seed’ patterns, global configuration of tree-seed locations, and overall resulting ‘global-forest’ patterns have fractal qualities. These designs span multiple mediums yet are all intended to lower occupant stress without detracting from the function and overall design of the space. In this series of studies, we first establish divergent relationships between various visual attributes, with pattern complexity, preference, and engagement ratings increasing with fractal complexity compared to ratings of refreshment and relaxation which stay the same or decrease with complexity. Subsequently, we determine that the local constituent fractal (‘tree-seed’) patterns contribute to the perception of the overall fractal design, and address how to balance aesthetic and psychological effects (such as individual experiences of perceived engagement and relaxation) in fractal design installations. This set of studies demonstrates that fractal preference is driven by a balance between increased arousal (desire for engagement and complexity) and decreased tension (desire for relaxation or refreshment). Installations of these composite mid-high complexity ‘global-forest’ patterns consisting of ‘tree-seed’ components balance these contrasting needs, and can serve as a practical implementation of biophilic patterns in human-made environments to promote occupant well-being.

• 
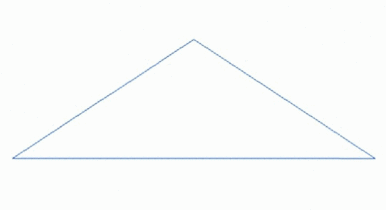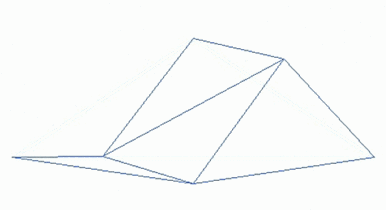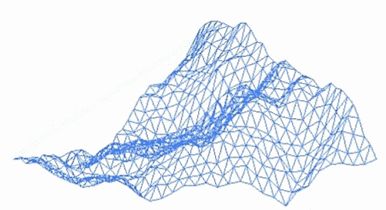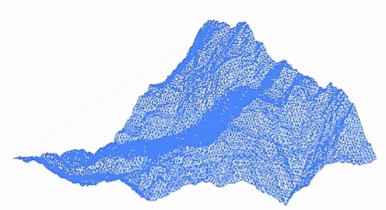
  A fractal that models the surface of a mountain (animation)
• 
  3D recursive image
• 
  Recursive fractal butterfly image
• 
  A fractal flame

Physiological responses

Humans appear to be especially well-adapted to processing fractal patterns with fractal dimension between 1.3 and 1.5.^[85] When humans view fractal patterns with fractal dimension between 1.3 and 1.5, this tends to reduce physiological stress.^[86][87]

Applications in technology

Main article: Fractal analysis

• Fractal antennas^[88]
• Fractal transistor^[89]
• Fractal heat exchangers^[90]
• Digital imaging
• Architecture^[28]
• Urban growth^[91][92]
• Classification of histopathology
  slides
• Fractal landscape or Coastline complexity
• Detecting 'life as we don't know it' by fractal analysis^[93]
• Enzymes (Michaelis–Menten kinetics)
• Generation of new music
• Signal and image compression
• Creation of digital photographic enlargements
• Fractal in soil mechanics
• Computer and video game design
• Computer Graphics
• Organic environments
• Procedural generation
• Fractography and fracture mechanics
• Small angle scattering theory of fractally rough systems
• T-shirts and other fashion
• Generation of patterns for camouflage, such as MARPAT
• Digital sundial
• Technical analysis of price series
• Fractals in networks
• Medicine^[24]
• Neuroscience^[19][20]
• Diagnostic Imaging^[23]
• Pathology^[94][95]
• Geology^[96]
• Geography^[97]
• Archaeology^[98][99]
• Soil mechanics^[22]
• Seismology^[25]
• Search and rescue^[100]
• cache coherency in texture mapping,^{[101][102][103]} rasterisation^[104][105] and indexing of turbulence data.^[106][107]

See also

• Banach fixed point theorem
   – Theorem about metric spacesPages displaying short descriptions of redirect targets
• Bifurcation theory – Study of sudden qualitative behavior changes caused by small parameter changes
• Box counting – Fractal analysis technique
• Cymatics – Creation of visible patterns on a vibrated plate
• Determinism – Philosophical view that events are determined by prior events
• Diamond-square algorithm – Method for generating heightmaps for computer graphics
• Droste effect – Recursive visual effect
• Feigenbaum function
• Form constant – Recurringly observed geometric pattern
• Fractal cosmology – Absolute Infinite Everything
• Fractal derivative – Generalization of derivative to fractals
• Fractalgrid
• Fractal string
• Fracton – Synonym of phonon
• Graftal
   – Rewriting system and type of formal grammarPages displaying short descriptions of redirect targets
• Greeble – Fine relief detailing added to a surface to make it appear more complex
• Infinite regress – Philosophical problem
• Lacunarity – Term in geometry and fractal analysis
• List of fractals by Hausdorff dimension
• Mandelbulb – Three-dimensional fractal
• Mandelbox – Fractal with a boxlike shape
• Macrocosm and microcosm
   – Analogy between man and cosmosPages displaying short descriptions of redirect targets
• Matryoshka doll – Russian nested wooden toy
• Menger Sponge
   – Three-dimensional fractalPages displaying short descriptions of redirect targets
• Multifractal system – System with multiple fractal dimensions
• Newton fractal – Boundary set in the complex plane
• Percolation – Filtration of fluids through porous materials
• Power law – Functional relationship between two quantities
• Publications in fractal geometry
• Random walk – Mathematical formalization of a path that consists of a succession of random steps
• Self-reference – Sentence, idea or formula that refers to itself
• Self-similarity – Whole of an object being mathematically similar to part of itself
• Systems theory – Interdisciplinary study of systems
• Strange loop – Cyclic structure that goes through several levels in a hierarchical system
• Turbulence – Motion characterized by chaotic changes in pressure and flow velocity
• Wiener process – Stochastic process generalizing Brownian motion

Notes

1. ^ The original paper, Lévy, Paul (1938). "Les Courbes planes ou gauches et les surfaces composées de parties semblables au tout". Journal de l'École Polytechnique: 227–247, 249–291., is translated in Edgar, pages 181–239.
2. ^ The Hilbert curve map is not a homeomorphism, so it does not preserve topological dimension. The topological dimension and Hausdorff dimension of the image of the Hilbert map in R² are both 2. Note, however, that the topological dimension of the graph of the Hilbert map (a set in R³) is 1.

References

1. ^
   ISBN 978-0-7167-1186-5
   .
2. ^
   ISBN 978-0-470-84862-3
   .
3. ^
   ISBN 978-0-500-27693-8
   .
4. ^
   ISBN 978-981-02-0668-0
   .
5. ^
   ISBN 978-0-387-94153-0
   .
6. ^
   ISBN 978-0-387-20158-0
   . A fractal set is one for which the fractal (Hausdorff-Besicovitch) dimension strictly exceeds the topological dimension
7. S2CID 120037858
   .
8. ^
   ISBN 978-0-8133-4153-8
   .
9. ^ ^{a b c d e f g h i} Trochet, Holly (2009). "A History of Fractal Geometry". MacTutor History of Mathematics. Archived from the original on March 12, 2012.
10. ^ Mandelbrot, Benoit. "24/7 Lecture on Fractals". 2006 Ig Nobel Awards. Improbable Research. Archived from the original on December 11, 2021.
11. ^ Mandelbrot, B. B.: The Fractal Geometry of Nature. W. H. Freeman and Company, New York (1982); p. 15.
12. ISBN 978-0-387-74749-1
    .
13. ^
    ISBN 978-0-471-13938-6
    .
14. doi:10.1016/0375-9601(94)91220-3
    .
15. doi:10.1016/0375-9601(95)00727-k
    .
16. S2CID 14494072
    .
17. ^
    doi:10.1142/S0218348X0700337X
    .
18. ^
    PMID 19528254
    .
19. ^
    PMID 14645092
    .
20. ^
    doi:10.1142/S0218348X08003880
    .
21. ^
    OCLC 224846454
    . Retrieved February 3, 2012. Event location: Canberra, Australia
22. ^
    doi:10.1016/j.apgeog.2011.10.016
    .
23. ^
    PMID 19668394
    .
24. ^
    ISBN 978-3-7643-7172-2
    .
25. ^
    S2CID 128467785
    .
26. ^ ^{a b} Wallace, David Foster (August 4, 2006). "Bookworm on KCRW". Kcrw.com. Archived from the original on November 11, 2010. Retrieved October 17, 2010.
27. ^ ^{a b} Eglash, Ron (1999). "African Fractals: Modern Computing and Indigenous Design". New Brunswick: Rutgers University Press. Archived from the original on January 3, 2018. Retrieved October 17, 2010.
28. ^
    doi:10.1007/978-3-319-32426-5
    .
29. ^ Baranger, Michael. "Chaos, Complexity, and Entropy: A physics talk for non-physicists" (PDF).
30. ^ Benoît Mandelbrot, Objets fractals, 1975, p. 4
31. ^
    ISBN 978-1-56881-340-0
    .
32. ^ "fractal". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
33. ^
    ISBN 978-1-84046-123-7
    .
34. ISBN 978-0-8135-2613-3
    .
35. ^
    ISBN 978-1-4027-5796-9
    .
36. ^ "Fractal Geometry". www-history.mcs.st-and.ac.uk. Retrieved April 11, 2017.
37. S2CID 15662830. Archived from the original
    on October 19, 2021. Retrieved October 31, 2020.
38. ^ Batty, Michael (April 4, 1985). "Fractals – Geometry Between Dimensions". New Scientist. 105 (1450): 31.
39. ISBN 978-0-306-44702-0
    . Retrieved February 5, 2011.
40. ^ "Vol Libre, an amazing CG film from 1980". kottke.org. July 29, 2009. Retrieved February 12, 2023.
41. ISBN 978-0-387-74748-4
    .
42. doi:10.13140/2.1.2815.9048
    .
43. ISBN 978-0-19-530059-8
    .
44. ISBN 978-0-444-50002-1
    . Retrieved February 4, 2012.
45. ^ "Haferman Carpet". WolframAlpha. Retrieved October 18, 2012.
46. ^
    ISBN 978-3-7643-7172-2
    .
47. ^ J. W. Cannon, W. J. Floyd, W. R. Parry. Finite subdivision rules. Conformal Geometry and Dynamics, vol. 5 (2001), pp. 153–196.
48. ISBN 978-981-02-3792-9
    .
49. doi:10.1142/S0218348X11005476
    .
50. ^ "Hunting the Hidden Dimensional". Nova. PBS. WPMB-Maryland. October 28, 2008.
51. PMID 28690919
    .
52. ^ Falconer, Kenneth (2013). Fractals, A Very Short Introduction. Oxford University Press.
53. S2CID 32255821
    .
54. ISBN 978-981-02-3792-9
    .
55. PMID 31227758
56. ISBN 978-3-540-40754-6
    .
57. ^
    S2CID 4361904
58. S2CID 235508504
    .
59. S2CID 14482711
    .
60. PMID 27388607
    .
61. ISBN 978-0-7503-0400-9
    . Retrieved February 5, 2011.
62. PMID 15697635
    .
63. S2CID 4158401
    .
64. ISBN 978-0-7190-3434-3
    .
65. PMID 25883885
    .
66. ISBN 978-2-86332-130-0
    . Retrieved February 5, 2011.
67. ^ Ozhovan M. I., Dmitriev I. E., Batyukhnova O. G. Fractal structure of pores of clay soil. Atomic Energy, 74, 241–243 (1993).
68. S2CID 55578215
    .
69. S2CID 22560587
    .
70. PMID 31413194
    .
71. S2CID 3811866
    .
72. S2CID 23274235
    .
73. S2CID 52010780
    .
74. S2CID 204993516
    .
75. S2CID 31353634
    .
76. S2CID 8529592
    .
77. doi:10.1504/IJART.2015.067389. Archived from the original
    (PDF) on October 25, 2017. Retrieved October 24, 2017.
78. PMID 21734876
    .
79. ^ Frame, Michael; and Mandelbrot, Benoît B.; A Panorama of Fractals and Their Uses Archived December 23, 2007, at the Wayback Machine
80. ^ Nelson, Bryn (February 23, 2000). "Sophisticated Mathematics Behind African Village Designs / Fractal patterns use repetition on large, small scale". SFGATE. Retrieved February 12, 2023.
81. ISBN 978-979-22-4484-7
82. ^ Rulistia, Novia D. (October 6, 2015). "Application maps out nation's batik story". The Jakarta Post. Retrieved September 25, 2016.
83. ^ Koutonin, Mawuna (March 18, 2016). "Story of cities #5: Benin City, the mighty medieval capital now lost without trace". Retrieved April 2, 2018.
84. PMID 34484047
    .
85. ISBN 978-1-4939-3995-4
    .
86. S2CID 8495221
    .
87. PMID 21734876
    .
88. doi:10.1142/S0218348X99000098
    .
89. S2CID 43053855.{{cite book}}: CS1 maint: date and year (link
    )
90. ^ Zhiwei Huang; Yunho Hwang; Vikrant Aute; Reinhard Radermacher (2016). "Review of Fractal Heat Exchangers" (PDF) International Refrigeration and Air Conditioning Conference. Paper 1725{{cite web}}: CS1 maint: postscript (link)
91. PMID 21949753
    .
92. ^ "Applications". Archived from the original on October 12, 2007. Retrieved October 21, 2007.
93. S2CID 122793675
    .
94. PMID 2716356
    .
95. S2CID 40311727
    .
96. S2CID 118918429
    .
97. PMID 21949753
    .
98. PMID 16393505
    .
99. S2CID 7481018
    .
100. ISBN 978-988-17-0125-1
     .
101. ^ "GPU internals" (PDF).
102. ^ "sony patents".
103. ^ "description of swizzled and hybrid tiled swizzled textures".
104. ^ "US8773422B1 - System, method, and computer program product for grouping linearly ordered primitives". Google Patents. December 4, 2007. Retrieved December 28, 2019.
105. ^ "US20110227921A1 - Processing of 3D computer graphics data on multiple shading engines". Google Patents. December 15, 2010. Retrieved December 27, 2019.
106. ^ "Johns Hopkins Turbulence Databases".
107. S2CID 15768582
     .

Further reading

• Barnsley, Michael F.; and Rising, Hawley; Fractals Everywhere. Boston: Academic Press Professional, 1993.
  ISBN 0-12-079061-0
• Duarte, German A.; Fractal Narrative. About the Relationship Between Geometries and Technology and Its Impact on Narrative Spaces. Bielefeld: Transcript, 2014.
  ISBN 978-3-8376-2829-6
• Falconer, Kenneth; Techniques in Fractal Geometry. John Wiley and Sons, 1997.
  ISBN 0-471-92287-0
• Jürgens, Hartmut;
  ISBN 0-387-97903-4
• ISBN 0-7167-1186-9
• Peitgen, Heinz-Otto; and Saupe, Dietmar; eds.; The Science of Fractal Images. New York: Springer-Verlag, 1988.
  ISBN 0-387-96608-0
• ISBN 0-444-50002-2
• Jones, Jesse; Fractals for the Macintosh, Waite Group Press, Corte Madera, CA, 1993.
  ISBN 1-878739-46-8
  .
• Lauwerier, Hans; Fractals: Endlessly Repeated Geometrical Figures, Translated by Sophia Gill-Hoffstadt, Princeton University Press, Princeton NJ, 1991.
  ISBN 0-691-02445-6
  paperback. "This book has been written for a wide audience..." Includes sample BASIC programs in an appendix.
• Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press.
  ISBN 978-0-19-850839-7
  .
• Wahl, Bernt; Van Roy, Peter; Larsen, Michael; and Kampman, Eric; Exploring Fractals on the Macintosh, Addison Wesley, 1995.
  ISBN 0-201-62630-6
• Lesmoir-Gordon, Nigel; The Colours of Infinity: The Beauty, The Power and the Sense of Fractals. 2004.
  ISBN 1-904555-05-5 (The book comes with a related DVD of the Arthur C. Clarke documentary introduction to the fractal concept and the Mandelbrot set
  .)
• Liu, Huajie; Fractal Art, Changsha: Hunan Science and Technology Press, 1997,
  ISBN 9787535722348
  .
• Gouyet, Jean-François; Physics and Fractal Structures (Foreword by B. Mandelbrot); Masson, 1996.
  ISBN 978-0-387-94153-0. Out-of-print. Available in PDF version at."Physics and Fractal Structures"
  (in French). Jfgouyet.fr. Retrieved October 17, 2010.
• Falconer, Kenneth (2013). Fractals, A Very Short Introduction. Oxford University Press.

External links

Wikimedia Commons has media related to Fractal.

Wikibooks has a book on the topic of: Fractals

• Fractals at the Library of Congress Web Archives (archived November 16, 2001)
• "Hunting the Hidden Dimension",
  NOVA
  , first aired August 24, 2011
• Benoit Mandelbrot: Fractals and the Art of Roughness (Archived February 17, 2014, at the Wayback Machine), TED, February 2010
• Technical Library on Fractals for controlling fluid
• Equations of self-similar fractal measure based on the fractional-order calculus（2007）