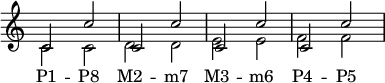Interval (music)

In music theory, an interval is a difference in pitch between two sounds.^[1] An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.^[2][3]

In

notes such as C♯ and D♭. Intervals can be arbitrarily small, and even imperceptible to the human ear.

In physical terms, an interval is the ratio between two sonic frequencies. For example, any two notes an octave apart have a frequency ratio of 2:1. This means that successive increments of pitch by the same interval result in an exponential increase of frequency, even though the human ear perceives this as a linear increase in pitch. For this reason, intervals are often measured in cents, a unit derived from the logarithm of the frequency ratio.

In Western music theory, the most common naming scheme for intervals describes two properties of the interval: the

Size

The size of an interval (also known as its width or height) can be represented using two alternative and equivalently valid methods, each appropriate to a different context: frequency ratios or cents.

Frequency ratios

The size of an interval between two notes may be measured by the

). Intervals with small-integer ratios are often called just intervals, or pure intervals.

Most commonly, however, musical instruments are nowadays tuned using a different tuning system, called

.

Cents

The standard system for comparing interval sizes is with cents. The cent is a logarithmic unit of measurement. If frequency is expressed in a logarithmic scale, and along that scale the distance between a given frequency and its double (also called octave) is divided into 1200 equal parts, each of these parts is one cent. In twelve-tone equal temperament (12-TET), a tuning system in which all semitones have the same size, the size of one semitone is exactly 100 cents. Hence, in 12-TET the cent can be also defined as one hundredth of a semitone.

Mathematically, the size in cents of the interval from frequency f₁ to frequency f₂ is

Main intervals

The table shows the most widely used conventional names for the intervals between the notes of a

), or more strictly as a synonym of major third.

Intervals with different names may span the same number of semitones, and may even have the same width. For instance, the interval from D to F♯ is a major third, while that from D to G♭ is a diminished fourth. However, they both span 4 semitones. If the instrument is tuned so that the 12 notes of the chromatic scale are equally spaced (as in equal temperament), these intervals also have the same width. Namely, all semitones have a width of 100 cents, and all intervals spanning 4 semitones are 400 cents wide.

The names listed here cannot be determined by counting semitones alone. The rules to determine them are explained below. Other names, determined with different naming conventions, are listed in a separate section. Intervals smaller than one semitone (commas or microtones) and larger than one octave (compound intervals) are introduced below.

Number of semitones	Minor, major, or perfect intervals	Short	Augmented or diminished intervals	Short	Widely used alternative names	Short	Audio
0	Perfect unison	P1	Diminished second	d2			Playⓘ
1	Minor second	m2	Augmented unison	A1	Semitone, half tone, half step	S	Playⓘ
2	Major second	M2	Diminished third	d3	Tone , whole tone, whole step	T	Playⓘ
3	Minor third	m3	Augmented second	A2			Playⓘ
4	Major third	M3	Diminished fourth	d4			Playⓘ
5	Perfect fourth	P4	Augmented third	A3			Playⓘ
6			Diminished fifth	d5	Tritone	TT	Playⓘ
			Augmented fourth	A4
7	Perfect fifth	P5	Diminished sixth	d6			Playⓘ
8	Minor sixth	m6	Augmented fifth	A5			Playⓘ
9	Major sixth	M6	Diminished seventh	d7			Playⓘ
10	Minor seventh	m7	Augmented sixth	A6			Playⓘ
11	Major seventh	M7	Diminished octave	d8			Playⓘ
12	Perfect octave	P8	Augmented seventh	A7			Playⓘ

Interval number and quality

In Western music theory, an interval is named according to its number (also called diatonic number) and quality. For instance, major third (or M3) is an interval name, in which the term major (M) describes the quality of the interval, and third (3) indicates its number.

Number

staff positions

indicated

The number of an interval is the number of letter names or

.

There is a

This means that interval numbers can also be determined by counting diatonic scale degrees, rather than staff positions, provided that the two notes that form the interval are drawn from a diatonic scale. Namely, C–G is a fifth because in any diatonic scale that contains C and G, the sequence from C to G includes five notes. For instance, in the A♭-major diatonic scale, the five notes are C–D♭–E♭–F–G (see figure). This is not true for all kinds of scales. For instance, in a chromatic scale, the notes from C to G are eight (C–C♯–D–D♯–E–F–F♯–G). This is the reason interval numbers are also called diatonic numbers, and this convention is called diatonic numbering.

If one adds any accidentals to the notes that form an interval, by definition the notes do not change their staff positions. As a consequence, any interval has the same interval number as the corresponding natural interval, formed by the same notes without accidentals. For instance, the intervals C–G♯ (spanning 8 semitones) and C♯–G (spanning 6 semitones) are fifths, like the corresponding natural interval C–G (7 semitones).

Notice that interval numbers represent an inclusive count of encompassed staff positions or note names, not the difference between the endpoints. In other words, one starts counting the lower pitch as one, not zero. For that reason, the interval C–C, a perfect unison, is called a prime (meaning "1"), even though there is no difference between the endpoints. Continuing, the interval C–D is a second, but D is only one staff position, or diatonic-scale degree, above C. Similarly, C–E is a third, but E is only two staff positions above C, and so on. As a consequence, joining two intervals always yields an interval number one less than their sum. For instance, the intervals C–E and E–G are thirds, but joined together they form a fifth (C–G), not a sixth. Similarly, a stack of three thirds, such as C–E, E–G, and G–B, is a seventh (C–B), not a ninth.

This scheme applies to intervals up to an octave (12 semitones). For larger intervals, see § Compound intervals below.

Quality

The name of any interval is further qualified using the terms perfect (P),

.

Perfect

Perfect intervals are so-called because they were traditionally considered perfectly consonant,^[6] although in Western classical music the perfect fourth was sometimes regarded as a less than perfect consonance, when its function was contrapuntal.^[vague] Conversely, minor, major, augmented or diminished intervals are typically considered less consonant, and were traditionally classified as mediocre consonances, imperfect consonances, or dissonances.^[6]

Within a diatonic scale^[b] all unisons (P1) and octaves (P8) are perfect. Most fourths and fifths are also perfect (P4 and P5), with five and seven semitones respectively. One occurrence of a fourth is augmented (A4) and one fifth is diminished (d5), both spanning six semitones. For instance, in a C-major scale, the A4 is between F and B, and the d5 is between B and F (see table).

By definition, the inversion of a perfect interval is also perfect. Since the inversion does not change the pitch class of the two notes, it hardly affects their level of consonance (matching of their harmonics). Conversely, other kinds of intervals have the opposite quality with respect to their inversion. The inversion of a major interval is a minor interval, the inversion of an augmented interval is a diminished interval.

Major and minor

As shown in the table, a diatonic scale^[b] defines seven intervals for each interval number, each starting from a different note (seven unisons, seven seconds, etc.). The intervals formed by the notes of a diatonic scale are called diatonic. Except for unisons and octaves, the diatonic intervals with a given interval number always occur in two sizes, which differ by one semitone. For example, six of the fifths span seven semitones. The other one spans six semitones. Four of the thirds span three semitones, the others four. If one of the two versions is a perfect interval, the other is called either diminished (i.e. narrowed by one semitone) or augmented (i.e. widened by one semitone). Otherwise, the larger version is called major, the smaller one minor. For instance, since a 7-semitone fifth is a perfect interval (P5), the 6-semitone fifth is called "diminished fifth" (d5). Conversely, since neither kind of third is perfect, the larger one is called "major third" (M3), the smaller one "minor third" (m3).

Within a diatonic scale,^[b] unisons and octaves are always qualified as perfect, fourths as either perfect or augmented, fifths as perfect or diminished, and all the other intervals (seconds, thirds, sixths, sevenths) as major or minor.

Augmented and diminished

Augmented intervals are wider by one semitone than perfect or major intervals, while having the same interval number (i.e., encompassing the same number of staff positions): they are wider by a

. Diminished intervals, on the other hand, are narrower by one semitone than perfect or minor intervals of the same interval number: they are narrower by a chromatic semitone. For instance, an augmented third such as C–E♯ spans five semitones, exceeding a major third (C–E) by one semitone, while a diminished third such as C♯–E♭ spans two semitones, falling short of a minor third (C–E♭) by one semitone.

The augmented fourth (A4) and the diminished fifth (d5) are the only augmented and diminished intervals that appear in diatonic scales^[b] (see table).

Example

Neither the number, nor the quality of an interval can be determined by counting

alone. As explained above, the number of staff positions must be taken into account as well.

For example, as shown in the table below, there are four semitones between A♭ and B♯, between A and C♯, between A and D♭, and between A♯ and E, but

• A♭–B♯ is a second, as it encompasses two staff positions (A, B), and it is doubly augmented, as it exceeds a major second (such as A–B) by two semitones.
• A–C♯ is a third, as it encompasses three staff positions (A, B, C), and it is major, as it spans 4 semitones.
• A–D♭ is a fourth, as it encompasses four staff positions (A, B, C, D), and it is diminished, as it falls short of a perfect fourth (such as A–D) by one semitone.
• A♯-E is a fifth, as it encompasses five staff positions (A, B, C, D, E), and it is triply diminished, as it falls short of a perfect fifth (such as A–E) by three semitones.

Number of semitones	Interval name	Staff positions
		1	2	3	4	5
4	doubly augmented second (AA2)	A♭	B♯
4	major third (M3)	A		C♯
4	diminished fourth (d4)	A			D♭
4	triply diminished fifth (ddd5)	A♯				E

Shorthand notation

Intervals are often abbreviated with a P for perfect, m for minor, M for major, d for diminished, A for augmented, followed by the interval number. The indications M and P are often omitted. The octave is P8, and a unison is usually referred to simply as "a unison" but can be labeled P1. The tritone, an augmented fourth or diminished fifth is often TT. The interval qualities may be also abbreviated with perf, min, maj, dim, aug. Examples:

• m2 (or min2): minor second,
• M3 (or maj3): major third,
• A4 (or aug4): augmented fourth,
• d5 (or dim5): diminished fifth,
• P5 (or perf5): perfect fifth.

Inversion

A simple interval (i.e., an interval smaller than or equal to an octave) may be inverted by raising the lower pitch an octave or lowering the upper pitch an octave. For example, the fourth from a lower C to a higher F may be inverted to make a fifth, from a lower F to a higher C.

There are two rules to determine the number and quality of the inversion of any simple interval:^[7]

1. The interval number and the number of its inversion always add up to nine (4 + 5 = 9, in the example just given).
2. The inversion of a major interval is a minor interval, and vice versa; the inversion of a perfect interval is also perfect; the inversion of an augmented interval is a diminished interval, and vice versa; the inversion of a doubly augmented interval is a doubly diminished interval, and vice versa.

For example, the interval from C to the E♭ above it is a minor third. By the two rules just given, the interval from E♭ to the C above it must be a major sixth.

Since compound intervals are larger than an octave, "the inversion of any compound interval is always the same as the inversion of the simple interval from which it is compounded".^[8]

For intervals identified by their ratio, the inversion is determined by reversing the ratio and multiplying the ratio by 2 until it is greater than 1. For example, the inversion of a 5:4 ratio is an 8:5 ratio.

For intervals identified by an integer number of semitones, the inversion is obtained by subtracting that number from 12.

Since an interval class is the lower number selected among the interval integer and its inversion, interval classes cannot be inverted.

Classification

Intervals can be described, classified, or compared with each other according to various criteria.

Melodic and harmonic

An interval can be described as

• Vertical or harmonic if the two notes sound simultaneously
• Horizontal, linear, or melodic if they sound successively.^[2] Melodic intervals can be ascending (lower pitch precedes higher pitch) or descending.

Diatonic and chromatic

In general,

• A
  diatonic interval is an interval formed by two notes of a diatonic scale
  .
• A chromatic interval is a non-diatonic interval formed by two notes of a chromatic scale.

The table above depicts the 56 diatonic intervals formed by the notes of the C major scale (a diatonic scale). Notice that these intervals, as well as any other diatonic interval, can be also formed by the notes of a chromatic scale.

The distinction between diatonic and chromatic intervals is controversial, as it is based on the definition of diatonic scale, which is variable in the literature. For example, the interval B–E♭ (a diminished fourth, occurring in the harmonic C-minor scale) is considered diatonic if the harmonic minor scales are considered diatonic as well.^[9] Otherwise, it is considered chromatic. For further details, see the main article.

By a commonly used definition of diatonic scale

scales), all perfect, major and minor intervals are diatonic. Conversely, no augmented or diminished interval is diatonic, except for the augmented fourth and diminished fifth.

The distinction between diatonic and chromatic intervals may be also sensitive to context. The above-mentioned 56 intervals formed by the C-major scale are sometimes called diatonic to C major. All other intervals are called chromatic to C major. For instance, the perfect fifth A♭–E♭ is chromatic to C major, because A♭ and E♭ are not contained in the C major scale. However, it is diatonic to others, such as the A♭ major scale.

Consonant and dissonant

Consonance and dissonance are relative terms that refer to the stability, or state of repose, of particular musical effects. Dissonant intervals are those that cause tension and desire to be resolved to consonant intervals.

These terms are relative to the usage of different compositional styles.

• In 15th- and 16th-century usage, perfect fifths and octaves, and major and minor thirds and sixths were considered harmonically consonant, and all other intervals dissonant, including the perfect fourth, which by 1473 was described (by Johannes Tinctoris) as dissonant, except between the upper parts of a vertical sonority—for example, with a supporting third below ("6-3 chords").^[10] In the common practice period, it makes more sense to speak of consonant and dissonant chords, and certain intervals previously considered dissonant (such as minor sevenths) became acceptable in certain contexts. However, 16th-century practice was still taught to beginning musicians throughout this period.
• Hermann von Helmholtz (1821–1894) theorised that dissonance was caused by the presence of beats.^[11] Helmholtz further believed that the beating produced by the upper partials of harmonic sounds was the cause of dissonance for intervals too far apart to produce beating between the fundamentals.^[12] Helmholtz then designated that two harmonic tones that shared common low partials would be more consonant, as they produced less beats.^[13][14] Helmholtz disregarded partials above the seventh, as he believed that they were not audible enough to have significant effect.^[15] From this Helmholtz categorises the octave, perfect fifth, perfect fourth, major sixth, major third, and minor third as consonant, in decreasing value, and other intervals as dissonant.
• David Cope (1997) suggests the concept of interval strength,^[16] in which an interval's strength, consonance, or stability is determined by its approximation to a lower and stronger, or higher and weaker, position in the harmonic series. See also: Lipps–Meyer law and #Interval root

All of the above analyses refer to vertical (simultaneous) intervals.

Simple and compound

A simple interval is an interval spanning at most one octave (see Main intervals above). Intervals spanning more than one octave are called compound intervals, as they can be obtained by adding one or more octaves to a simple interval (see below for details).^[17]

Steps and skips

Linear (melodic) intervals may be described as steps or skips. A step, or conjunct motion,^[18] is a linear interval between two consecutive notes of a scale. Any larger interval is called a skip (also called a leap), or disjunct motion.

or larger being skips.

For example, C to D (major second) is a step, whereas C to E (major third) is a skip.

More generally, a step is a smaller or narrower interval in a musical line, and a skip is a wider or larger interval, where the categorization of intervals into steps and skips is determined by the tuning system and the pitch space used.

Melodic motion in which the interval between any two consecutive pitches is no more than a step, or, less strictly, where skips are rare, is called stepwise or conjunct melodic motion, as opposed to skipwise or disjunct melodic motions, characterized by frequent skips.

Enharmonic intervals

Two intervals are considered enharmonic, or enharmonically equivalent, if they both contain the same pitches spelled in different ways; that is, if the notes in the two intervals are themselves enharmonically equivalent. Enharmonic intervals span the same number of semitones.

For example, the four intervals listed in the table below are all enharmonically equivalent, because the notes F♯ and G♭ indicate the same pitch, and the same is true for A♯ and B♭. All these intervals span four semitones.

Number of semitones	Interval name	Staff positions
		1	2	3	4
4	major third	F♯		A♯
4	major third		G♭		B♭
4	diminished fourth	F♯			B♭
4	doubly augmented second		G♭	A♯

When played as isolated chords on a

of the notes these intervals incorporate is very different.

The discussion above assumes the use of the prevalent tuning system,

, all four intervals shown in the example above would be different.

Minute intervals

There are also a number of minute intervals not found in the chromatic scale or labeled with a diatonic function, which have names of their own. They may be described as

are approximate.

• A Pythagorean comma is the difference between twelve justly tuned perfect fifths and seven octaves. It is expressed by the frequency ratio 531441:524288 (23.5 cents).
• A syntonic comma is the difference between four justly tuned perfect fifths and two octaves plus a major third. It is expressed by the ratio 81:80 (21.5 cents).
• A septimal comma is 64:63 (27.3 cents), and is the difference between the Pythagorean or 3-limit "7th" and the "harmonic 7th".
• A diesis is generally used to mean the difference between three justly tuned major thirds and one octave. It is expressed by the ratio 128:125 (41.1 cents). However, it has been used to mean other small intervals: see diesis for details.
• A diaschisma is the difference between three octaves and four justly tuned perfect fifths plus two justly tuned major thirds. It is expressed by the ratio 2048:2025 (19.6 cents).
• A schisma (also skhisma) is the difference between five octaves and eight justly tuned fifths plus one justly tuned major third. It is expressed by the ratio 32805:32768 (2.0 cents). It is also the difference between the Pythagorean and syntonic commas. (A schismic major third is a schisma different from a just major third, eight fifths down and five octaves up, F♭ in C.)
• A kleisma is the difference between six minor thirds and one tritave or perfect twelfth (an octave plus a perfect fifth), with a frequency ratio of 15625:15552 (8.1 cents) (Play^ⓘ).
• A septimal kleisma is the amount that two major thirds of 5:4 and a septimal major third, or supermajor third, of 9:7 exceeds the octave. Ratio 225:224 (7.7 cents).
• A quarter tone is half the width of a semitone, which is half the width of a whole tone. It is equal to exactly 50 cents.

Compound intervals

A compound interval is an interval spanning more than one octave.^[17] Conversely, intervals spanning at most one octave are called simple intervals (see Main intervals below).

In general, a compound interval may be defined by a sequence or "stack" of two or more simple intervals of any kind. For instance, a major tenth (two staff positions above one octave), also called compound major third, spans one octave plus one major third.

Any compound interval can be always decomposed into one or more octaves plus one simple interval. For instance, a major seventeenth can be decomposed into two octaves and one major third, and this is the reason why it is called a compound major third, even when it is built by adding up four fifths.

The diatonic number DN_c of a compound interval formed from n simple intervals with diatonic numbers DN₁, DN₂, ..., DN_n, is determined by:

${\displaystyle DN_{c}=1+(DN_{1}-1)+(DN_{2}-1)+...+(DN_{n}-1),\ }$

which can also be written as:

${\displaystyle DN_{c}=DN_{1}+DN_{2}+...+DN_{n}-(n-1),\ }$

The quality of a compound interval is determined by the quality of the simple interval on which it is based. For instance, a compound major third is a major tenth (1+(8−1)+(3−1) = 10), or a major seventeenth (1+(8−1)+(8−1)+(3−1) = 17), and a compound perfect fifth is a perfect twelfth (1+(8−1)+(5−1) = 12) or a perfect nineteenth (1+(8−1)+(8−1)+(5−1) = 19). Notice that two octaves are a fifteenth, not a sixteenth (1+(8−1)+(8−1) = 15). Similarly, three octaves are a twenty-second (1+3×(8−1) = 22), and so on.

Main compound intervals

Number of semitones	Minor, major, or perfect intervals	Short	Augmented or diminished intervals	Short
12			Diminished ninth	d9
13	Minor ninth	m9	Augmented octave	A8
14	Major ninth	M9	Diminished tenth	d10
15	Minor tenth	m10	Augmented ninth	A9
16	Major tenth	M10	Diminished eleventh	d11
17	Perfect eleventh	P11	Augmented tenth	A10
18			Diminished twelfth	d12
			Augmented eleventh	A11
19	Tritave	P12	Diminished thirteenth	d13
20	Minor thirteenth	m13	Augmented twelfth	A12
21	Major thirteenth	M13	Diminished fourteenth	d14
22	Minor fourteenth	m14	Augmented thirteenth	A13
23	Major fourteenth	M14	Diminished fifteenth	d15
24	Perfect fifteenth or Double octave	P15	Augmented fourteenth	A14
25			Augmented fifteenth	A15

It is also worth mentioning here the major seventeenth (28 semitones)—an interval larger than two octaves that can be considered a multiple of a perfect fifth (7 semitones) as it can be decomposed into four perfect fifths (7 × 4 = 28 semitones), or two octaves plus a major third (12 + 12 + 4 = 28 semitones). Intervals larger than a major seventeenth seldom come up, most often being referred to by their compound names, for example "two octaves plus a fifth"^[19] rather than "a 19th".

Intervals in chords

Chords are sets of three or more notes. They are typically defined as the combination of intervals starting from a common note called the

Chords are classified based on the quality and number of the intervals that define them.

Chord qualities and interval qualities

The main chord qualities are

dominant

. The

symbols

used for chord quality are similar to those used for interval quality (see above). In addition, + or aug is used for augmented, ° or dim for diminished, ^ø for half diminished, and dom for dominant (the symbol − alone is not used for diminished).

Deducing component intervals from chord names and symbols

The main rules to decode chord names or symbols are summarized below. Further details are given at

Rules to decode chord names and symbols

.

1. For 3-note chords (
   main article
   for further details.
2. Without contrary information, a
   major triad) are implied. For instance, a C chord is a C major triad, and the name C minor seventh (Cm⁷) implies a minor 3rd by rule 1, a perfect 5th by this rule, and a minor 7th
   by definition (see below). This rule has one exception (see next rule).
3. When the fifth interval is
   diminished, the third must be minor.^[d]
   This rule overrides rule 2. For instance, Cdim⁷ implies a diminished 5th by rule 1, a minor 3rd by this rule, and a diminished 7th by definition (see below).
4. Names and symbols that contain only a plain interval number (e.g., "seventh chord") or the chord root and a number (e.g., "C seventh", or C⁷) are interpreted as follows:
   • If the number is 2, 4, 6, etc., the chord is a major
     names and symbols for added tone chords
     ).
   • If the number is 7, 9, 11, 13, etc., the chord is
     extended chords
     ).
   • If the number is 5, the chord (technically not a chord in the traditional sense, but a dyad) is a power chord. Only the root, a perfect fifth and usually an octave are played.

The table shows the intervals contained in some of the main chords (component intervals), and some of the symbols used to denote them. The interval qualities or numbers in

font can be deduced from chord name or symbol by applying rule 1. In symbol examples, C is used as chord root.

Main chords		Component intervals
Name	Symbol examples	Third	Fifth	Seventh
Major triad	C	M3	P5
	CM, or Cmaj	M3	P5
Minor triad	Cm, or Cmin	m3	P5
Augmented triad	C+, or Caug	M3	A5
Diminished triad	C°, or Cdim	m3	d5
Dominant seventh chord	C7, or Cdom7	M3	P5	m7
Minor seventh chord	Cm7, or Cmin7	m3	P5	m7
Major seventh chord	CM7, or Cmaj7	M3	P5	M7
Augmented seventh chord	C+7, Caug7, C7♯5, or C7aug5	M3	A5	m7
Diminished seventh chord	C°7, or Cdim7	m3	d5	d7
Half-diminished seventh chord	Cø7, Cm7♭5, or Cm7dim5	m3	d5	m7

Size of intervals used in different tuning systems

Number of semitones	Name	5-limit tuning (pitch ratio)	Comparison of interval width (in cents)
			5-limit tuning	Pythagorean tuning	1⁄4-comma meantone	Equal temperament
0	Perfect unison	1:1	0	0	0	0
1	Minor second	16:15 27:25	112 133	90	117	100
2	Major second	9:8 10:9	204 182	204	193	200
3	Minor third	6:5 32:27	316 294	294 318	310 (wolf) 269	300
4	Major third	5:4	386	408 384	386 (wolf) 427	400
5	Perfect fourth	4:3 27:20	498 520	498 (wolf) 522	503 (wolf) 462	500
6	Augmented fourth Diminished fifth	45:32 25:18	590 569	612 588	579 621	600
7	Perfect fifth	3:2 40:27	702 680	702 (wolf) 678	697 (wolf) 738	700
8	Minor sixth	8:5	814	792	814	800
9	Major sixth	5:3 27:16	884 906	906	890	900
10	Minor seventh	16:9 9:5	996 1018	996	1007	1000
11	Major seventh	15:8 50:27	1088 1067	1110	1083	1100
12	Perfect octave	2:1	1200	1200	1200	1200

In this table, the interval widths used in four different tuning systems are compared. To facilitate comparison,

one).

In

. 1⁄4-comma meantone was designed to produce just major thirds, but only 8 of them are just (5:4, about 386 cents).

The Pythagorean tuning is characterized by smaller differences because they are multiples of a smaller ε (ε ≈ 1.96 cents, the difference between the Pythagorean fifth and the average fifth). Notice that here the fifth is wider than 700 cents, while in most meantone temperaments, including 1⁄4-comma meantone, it is tempered to a size smaller than 700. A more detailed analysis is provided at Pythagorean tuning § Size of intervals.

The

).

The above-mentioned symmetric scale 1, defined in the 5-limit tuning system, is not the only method to obtain

5-limit tuning § The justest ratios

.

In the diatonic system, every interval has one or more enharmonic equivalents, such as augmented second for minor third.

Interval root

Although intervals are usually designated in relation to their lower note, David Cope^[16] and Hindemith^[21] both suggest the concept of interval root. To determine an interval's root, one locates its nearest approximation in the harmonic series. The root of a perfect fourth, then, is its top note because it is an octave of the fundamental in the hypothetical harmonic series. The bottom note of every odd diatonically numbered intervals are the roots, as are the tops of all even numbered intervals. The root of a collection of intervals or a chord is thus determined by the interval root of its strongest interval.

As to its usefulness, Cope

seventh chord (possibly the dominant of the mediant V/iii). According to the interval root of the strongest interval of the chord (in first inversion, CEGA), the perfect fifth (C–G), is the bottom C, the tonic.

Interval cycles

Interval cycles, "unfold [i.e., repeat] a single recurrent interval in a series that closes with a return to the initial pitch class", and are notated by George Perle using the letter "C", for cycle, with an interval-class integer to distinguish the interval. Thus the diminished-seventh chord would be C3 and the augmented triad would be C4. A superscript may be added to distinguish between transpositions, using 0–11 to indicate the lowest pitch class in the cycle.^[22]

Alternative interval naming conventions

As shown below, some of the above-mentioned intervals have alternative names, and some of them take a specific alternative name in

(or epimoric ratio). The same is true for the octave.

Typically, a comma is a diminished second, but this is not always true (for more details, see Alternative definitions of comma). For instance, in Pythagorean tuning the diminished second is a descending interval (524288:531441, or about −23.5 cents), and the Pythagorean comma is its opposite (531441:524288, or about 23.5 cents). 5-limit tuning defines four kinds of comma, three of which meet the definition of diminished second, and hence are listed in the table below. The fourth one, called syntonic comma (81:80) can neither be regarded as a diminished second, nor as its opposite. See Diminished seconds in 5-limit tuning for further details.

Number of semitones	Generic names				Specific names
	Quality and number		Other naming convention		Pythagorean tuning	5-limit tuning	1⁄4-comma meantone
	Full	Short
0	perfect unison or perfect prime	P1
	diminished second	d2			descending Pythagorean comma (524288:531441)	lesser diesis (128:125)
						diaschisma (2048:2025) greater diesis (648:625)
1	minor second	m2	semitone, half tone, half step	diatonic semitone, major semitone	limma (256:243)
	augmented unison or augmented prime	A1		chromatic semitone, minor semitone	apotome (2187:2048)
2	major second	M2	tone, whole tone , whole step		sesquioctavum (9:8)
3	minor third	m3				sesquiquintum (6:5)
4	major third	M3				sesquiquartum (5:4)
5	perfect fourth	P4			sesquitertium (4:3)
6	diminished fifth	d5	tritone[a]
	augmented fourth	A4
7	perfect fifth	P5			sesquialterum (3:2)
12	perfect octave	P8			duplex (2:1)

Additionally, some cultures around the world have their own names for intervals found in their music. For instance, 22 kinds of intervals, called shrutis, are canonically defined in Indian classical music.

Latin nomenclature

Up to the end of the 18th century, Latin was used as an official language throughout Europe for scientific and music textbooks. In music, many English terms are derived from Latin. For instance, semitone is from Latin semitonus.

The prefix semi- is typically used herein to mean "shorter", rather than "half".^[23][24][25] Namely, a semitonus, semiditonus, semidiatessaron, semidiapente, semihexachordum, semiheptachordum, or semidiapason, is shorter by one semitone than the corresponding whole interval. For instance, a semiditonus (3 semitones, or about 300 cents) is not half of a ditonus (4 semitones, or about 400 cents), but a ditonus shortened by one semitone. Moreover, in Pythagorean tuning (the most commonly used tuning system up to the 16th century), a semitritonus (d5) is smaller than a tritonus (A4) by one Pythagorean comma (about a quarter of a semitone).

Number of semitones	Quality and number	Short	Latin nomenclature
0	Perfect unison	P1	unisonus
1	Minor second	m2	semitonus
	Augmented unison	A1	unisonus superflua
2	Major second	M2	tonus
	Diminished third	d3
3	Minor third	m3	semiditonus
	Augmented second	A2	tonus superflua
4	Major third	M3	ditonus
	Diminished fourth	d4	semidiatessaron
5	Perfect fourth	P4	diatessaron
	Augmented third	A3	ditonus superflua
6	Diminished fifth	d5	semidiapente, semitritonus
	Augmented fourth	A4	tritonus
7	Perfect fifth	P5	diapente
	Diminished sixth	d6	semihexachordum
8	Minor sixth	m6	hexachordum minus, semitonus maius cum diapente, tetratonus
	Augmented fifth	A5	diapente superflua
9	Major sixth	M6	hexachordum maius, tonus cum diapente
	Diminished seventh	d7	semiheptachordum
10	Minor seventh	m7	heptachordum minus, semiditonus cum diapente, pentatonus
	Augmented sixth	A6	hexachordum superflua
11	Major seventh	M7	heptachordum maius, ditonus cum diapente
	Diminished octave	d8	semidiapason
12	Perfect octave	P8	diapason
	Augmented seventh	A7	heptachordum superflua

Non-diatonic intervals

Intervals in non-diatonic scales can be named using analogs of the diatonic interval names, by using a diatonic interval of similar size and distinguishing it by varying the quality, or by adding other modifiers. For example, the just interval 7/6 may be referred to as a subminor third, since it is ~267 cents wide, which is narrower than a minor third (300 cents in 12-TET, ~316 cents for the just interval 6/5), or as the

The most common of these extended qualities are a

neutral second, the characteristic interval of Arabic music, in 24-TET is 150 cents, exactly halfway between a minor second and major second. Combined, these yield the progression diminished, subminor, minor, neutral, major, supermajor, augmented for seconds, thirds, sixths, and sevenths. This naming convention can be extended to unisons, fourths, fifths, and octaves with sub and super, yielding the progression diminished, sub, perfect, super, augmented. This allows one to name all intervals in 24-TET or 31-TET, the latter of which was used by Adriaan Fokker. Various further extensions are used in Xenharmonic music.^[26]

Pitch-class intervals

Main articles:

Ordered pitch interval

In post-tonal or

integer notation is often used, most prominently in musical set theory

. In this system, intervals are named according to the number of half steps, from 0 to 11, the largest interval class being 6.

In atonal or musical set theory, there are numerous types of intervals, the first being the

ordered pitch interval

, the distance between two pitches upward or downward. For instance, the interval from C upward to G is 7, and the interval from G downward to C is −7. One can also measure the distance between two pitches without taking into account direction with the unordered pitch interval, somewhat similar to the interval of tonal theory.

The interval between pitch classes may be measured with ordered and unordered pitch-class intervals. The ordered one, also called directed interval, may be considered the measure upwards, which, since we are dealing with pitch classes, depends on whichever pitch is chosen as 0. For unordered pitch-class intervals, see interval class.^[27]

Generic and specific intervals

Main articles:

Generic interval

In

generic intervals

are distinguished. Specific intervals are the interval class or number of semitones between scale steps or collection members, and generic intervals are the number of diatonic scale steps (or staff positions) between notes of a collection or scale.

Notice that staff positions, when used to determine the conventional interval number (second, third, fourth, etc.), are counted including the position of the lower note of the interval, while generic interval numbers are counted excluding that position. Thus, generic interval numbers are smaller by 1, with respect to the conventional interval numbers.

Comparison

Specific interval		Generic interval	Diatonic name
Number of semitones	Interval class
0	0	0	Perfect unison
1	1	1	Minor second
2	2	1	Major second
3	3	2	Minor third
4	4	2	Major third
5	5	3	Perfect fourth
6	6	3 4	Augmented fourth Diminished fifth
7	5	4	Perfect fifth
8	4	5	Minor sixth
9	3	5	Major sixth
10	2	6	Minor seventh
11	1	6	Major seventh
12	0	7	Perfect octave

Generalizations and non-pitch uses

The term "interval" can also be generalized to other music elements besides pitch.

time points, timbres, or more abstract musical phenomena.^[28][29]

For example, an interval between two bell-like sounds, which have no pitch salience, is still perceptible. When two tones have similar acoustic spectra (sets of partials), the interval is just the distance of the shift of a tone spectrum along the frequency axis, so linking to pitches as reference points is not necessary. The same principle naturally applies to pitched tones (with similar harmonic spectra), which means that intervals can be perceived "directly" without pitch recognition. This explains in particular the predominance of interval hearing over absolute pitch hearing.^[30][31]

See also

• Circle of fifths
• Ear training
• List of meantone intervals
• List of pitch intervals
• Music and mathematics
• Pseudo-octave
• Regular temperament

Notes

1. ^ ^{a b} The term tritone is sometimes used more strictly as a synonym of augmented fourth (A4).
2. ^ ^{a b c d e f g} The expression
   melodic minor and the harmonic minor scales (see also Diatonic and chromatic
   ).
3. ^ ^{a b} General rule 1 achieves consistency in the interpretation of symbols such as CM⁷, Cm⁶, and C+⁷. Some musicians legitimately prefer to think that, in CM⁷, M refers to the seventh, rather than to the third. This alternative approach is legitimate, as both the third and seventh are major, yet it is inconsistent, as a similar interpretation is impossible for Cm⁶ and C+⁷ (in Cm⁶, m cannot possibly refer to the sixth, which is major by definition, and in C+⁷, + cannot refer to the seventh, which is minor). Both approaches reveal only one of the intervals (M3 or M7), and require other rules to complete the task. Whatever is the decoding method, the result is the same (e.g., CM⁷ is always conventionally decoded as C–E–G–B, implying M3, P5, M7). The advantage of rule 1 is that it has no exceptions, which makes it the simplest possible approach to decode chord quality.

   According to the two approaches, some may format the major seventh chord as CM⁷ (general rule 1: M refers to M3), and others as C^M7 (alternative approach: M refers to M7). Fortunately, even C^M7 becomes compatible with rule 1 if it is considered an abbreviation of CM^M7, in which the first M is omitted. The omitted M is the quality of the third, and is deduced according to rule 2 (see above), consistently with the interpretation of the plain symbol C, which by the same rule stands for CM.

4. ^ All triads are tertian chords (chords defined by sequences of thirds), and a major third would produce in this case a non-tertian chord. Namely, the diminished fifth spans 6 semitones from root, thus it may be decomposed into a sequence of two minor thirds, each spanning 3 semitones (m3 + m3), compatible with the definition of tertian chord. If a major third were used (4 semitones), this would entail a sequence containing a major second (M3 + M2 = 4 + 2 semitones = 6 semitones), which would not meet the definition of tertian chord.

References

Sources

• Longmans, Green, and Co.

External links

• Gardner, Carl E. (1912): Essentials of Music Theory, p. 38
• "Interval", Encyclopædia Britannica
• Lissajous Curves: Interactive simulation of graphical representations of musical intervals, beats, interference, vibrating strings
• Elements of Harmony: Vertical Intervals
• Just intervals, from the unison to the octave, played on a drone note on
  YouTube