Line (geometry)

plane |
|---|
| Geometers |
In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points (its endpoints).
Properties
In the Greek deductive geometry of Euclid's Elements, a general line (now called a curve) is defined as a "breadthless length", and a straight line (now called a line segment) was defined as a line "which lies evenly with the points on itself".[1]: 291 These definitions appeal to readers' physical experience, relying on terms that are not themselves defined, and the definitions are never explicitly referenced in the remainder of the text. In modern geometry, a line is usually either taken as a primitive notion with properties given by axioms,[1]: 95 or else defined as a set of points obeying a linear relationship, for instance when real numbers are taken to be primitive and geometry is established analytically in terms of numerical coordinates.
In an axiomatic formulation of Euclidean geometry, such as that of
On a Euclidean plane, a line can be represented as a boundary between two regions.[2]: 104 Any collection of finitely many lines partitions the plane into convex polygons (possibly unbounded); this partition is known as an arrangement of lines.
In higher dimensions
In
In more general Euclidean space, Rn (and analogously in every other affine space), the line L passing through two different points a and b is the subset
Collinear points
Three points are said to be collinear if they lie on the same line. Three points
In
Equivalently for three points in a plane, the points are collinear if and only if the slope between one pair of points equals the slope between any other pair of points (in which case the slope between the remaining pair of points will equal the other slopes). By extension, k points in a plane are collinear if and only if any (k–1) pairs of points have the same pairwise slopes.
In Euclidean geometry, the Euclidean distance d(a,b) between two points a and b may be used to express the collinearity between three points by:[3][4]
- The points a, b and c are collinear if and only if d(x,a) = d(c,a) and d(x,b) = d(c,b) implies x = c.
However, there are other notions of distance (such as the
In the geometries where the concept of a line is a primitive notion, as may be the case in some synthetic geometries, other methods of determining collinearity are needed.
Types

In a sense,[a] all lines in Euclidean geometry are equal, in that, without coordinates, one can not tell them apart from one another. However, lines may play special roles with respect to other objects in the geometry and be divided into types according to that relationship. For instance, with respect to a conic (a circle, ellipse, parabola, or hyperbola), lines can be:
- tangent lines, which touch the conic at a single point;
- secant lines, which intersect the conic at two points and pass through its interior;[5]
- exterior lines, which do not meet the conic at any point of the Euclidean plane; or
- a directrix, whose distance from a point helps to establish whether the point is on the conic.
- a coordinate line, a linear coordinate dimension
In the context of determining parallelism in Euclidean geometry, a transversal is a line that intersects two other lines that may or not be parallel to each other.
For more general algebraic curves, lines could also be:
- i-secant lines, meeting the curve in i points counted without multiplicity, or
- asymptotes, which a curve approaches arbitrarily closely without touching it.[6]
With respect to
- the Euler line,
- the Simson lines, and
- central lines.
For a convex quadrilateral with at most two parallel sides, the Newton line is the line that connects the midpoints of the two diagonals.[7]
For a
In three-dimensional space, skew lines are lines that are not in the same plane and thus do not intersect each other.
In axiomatic systems
The concept of line is often considered in geometry as a
In a non-axiomatic or simplified axiomatic treatment of geometry, the concept of a primitive notion may be too abstract to be dealt with. In this circumstance, it is possible to provide a description or mental image of a primitive notion, to give a foundation to build the notion on which would formally be based on the (unstated) axioms. Descriptions of this type may be referred to, by some authors, as definitions in this informal style of presentation. These are not true definitions, and could not be used in formal proofs of statements. The "definition" of line in Euclid's Elements falls into this category.[1]: 95 Even in the case where a specific geometry is being considered (for example, Euclidean geometry), there is no generally accepted agreement among authors as to what an informal description of a line should be when the subject is not being treated formally.
Definition
Linear equation
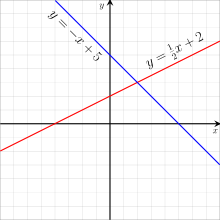
Lines in a Cartesian plane or, more generally, in
One can further suppose either c = 1 or c = 0, by dividing everything by c if it is not zero.
There are many variant ways to write the equation of a line which can all be converted from one to another by algebraic manipulation. The above form is sometimes called the standard form. If the constant term is put on the left, the equation becomes
These forms are generally named by the type of information (data) about the line that is needed to write down the form. Some of the important data of a line is its slope,
The equation of the line passing through two different points and may be written as
- m is the slope or gradient of the line.
- b is the y-intercept of the line.
- x is the independent variableof the function y = f(x).
The slope of the line through points and , when , is given by and the equation of this line can be written .
As a note, lines in three dimensions may also be described as the simultaneous solutions of two linear equations
Parametric equation
Parametric equations are also used to specify lines, particularly in those in three dimensions or more because in more than two dimensions lines cannot be described by a single linear equation.
In three dimensions lines are frequently described by parametric equations:
- x, y, and z are all functions of the independent variable t which ranges over the real numbers.
- (x0, y0, z0) is any point on the line.
- a, b, and c are related to the slope of the line, such that the direction vector(a, b, c) is parallel to the line.
Parametric equations for lines in higher dimensions are similar in that they are based on the specification of one point on the line and a direction vector.
Hesse normal form

The normal form (also called the Hesse normal form,[10] after the German mathematician Ludwig Otto Hesse), is based on the normal segment for a given line, which is defined to be the line segment drawn from the origin perpendicular to the line. This segment joins the origin with the closest point on the line to the origin. The normal form of the equation of a straight line on the plane is given by:
Unlike the slope-intercept and intercept forms, this form can represent any line but also requires only two finite parameters, and p, to be specified. If p > 0, then is uniquely defined modulo 2π. On the other hand, if the line is through the origin (c = p = 0), one drops the c/|c| term to compute and , and it follows that is only defined modulo π.
Other representations
Vectors
The vector equation of the line through points A and B is given by (where λ is a scalar).
If a is vector OA and b is vector OB, then the equation of the line can be written: .
A ray starting at point A is described by limiting λ. One ray is obtained if λ ≥ 0, and the opposite ray comes from λ ≤ 0.
Polar coordinates
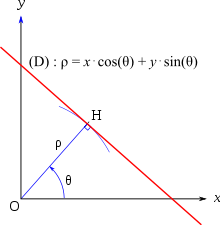
In a
In polar coordinates, the equation of a line not passing through the origin—the point with coordinates (0, 0)—can be written
It may be useful to express the equation in terms of the angle between the x-axis and the line. In this case, the equation becomes
These equations can be derived from the normal form of the line equation by setting and and then applying the
These equations can also be proven geometrically by applying right triangle definitions of sine and cosine to the right triangle that has a point of the line and the origin as vertices, and the line and its perpendicular through the origin as sides.
The previous forms do not apply for a line passing through the origin, but a simpler formula can be written: the polar coordinates of the points of a line passing through the origin and making an angle of with the x-axis, are the pairs such that
Generalizations of the Euclidean line
In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation, but in a more abstract setting, such as incidence geometry, a line may be an independent object, distinct from the set of points which lie on it.
When a geometry is described by a set of axioms, the notion of a line is usually left undefined (a so-called primitive object). The properties of lines are then determined by the axioms which refer to them. One advantage to this approach is the flexibility it gives to users of the geometry. Thus in differential geometry, a line may be interpreted as a geodesic (shortest path between points), while in some projective geometries, a line is a 2-dimensional vector space (all linear combinations of two independent vectors). This flexibility also extends beyond mathematics and, for example, permits physicists to think of the path of a light ray as being a line.
Projective geometry

In many models of
The "shortness" and "straightness" of a line, interpreted as the property that the distance along the line between any two of its points is minimized (see triangle inequality), can be generalized and leads to the concept of geodesics in metric spaces.
Extensions
Ray

Given a line and any point A on it, we may consider A as decomposing this line into two parts. Each such part is called a ray and the point A is called its initial point. It is also known as half-line, a one-dimensional half-space. The point A is considered to be a member of the ray.[b] Intuitively, a ray consists of those points on a line passing through A and proceeding indefinitely, starting at A, in one direction only along the line. However, in order to use this concept of a ray in proofs a more precise definition is required.
Given distinct points A and B, they determine a unique ray with initial point A. As two points define a unique line, this ray consists of all the points between A and B (including A and B) and all the points C on the line through A and B such that B is between A and C.[12] This is, at times, also expressed as the set of all points C on the line determined by A and B such that A is not between B and C.[13] A point D, on the line determined by A and B but not in the ray with initial point A determined by B, will determine another ray with initial point A. With respect to the AB ray, the AD ray is called the opposite ray.
Thus, we would say that two different points, A and B, define a line and a decomposition of this line into the disjoint union of an open segment (A, B) and two rays, BC and AD (the point D is not drawn in the diagram, but is to the left of A on the line AB). These are not opposite rays since they have different initial points.
In Euclidean geometry two rays with a common endpoint form an angle.[14]
The definition of a ray depends upon the notion of betweenness for points on a line. It follows that rays exist only for geometries for which this notion exists, typically Euclidean geometry or affine geometry over an ordered field. On the other hand, rays do not exist in projective geometry nor in a geometry over a non-ordered field, like the complex numbers or any finite field.
Line segment

A
Number line

A point on number line corresponds to a real number and vice versa.[15] Usually, integers are evenly spaced on the line, with positive numbers are on the right, negative numbers on the left. As an extension to the concept, an imaginary line representing imaginary numbers can be drawn perpendicular to the number line at zero.[16] The two lines forms the complex plane, a geometrical representation of the set of complex numbers.
See also
- Affine transformation
- Curve
- Distance between two parallel lines
- Distance from a point to a line
- Incidence (geometry)
- Line segment
- Generalised circle
- Locus
- Plane (geometry)
- Polyline
Notes
- transitivelyon the set of lines.
- ^ On occasion we may consider a ray without its initial point. Such rays are called open rays, in contrast to the typical ray which would be said to be closed.
References
- ^ ISBN 0-8247-1748-1
- OCLC 747274805.
- ^ Padoa, Alessandro (1900). Un nouveau système de définitions pour la géométrie euclidienne (in French). International Congress of Mathematicians.
- ^ Russell, Bertrand. The Principles of Mathematics. p. 410.
- ISBN 9780867200935.
- JSTOR 2690881
- )
- OCLC 47870
- ISBN 0-471-18283-4
- ^ Bôcher, Maxime (1915), Plane Analytic Geometry: With Introductory Chapters on the Differential Calculus, H. Holt, p. 44, archived from the original on 2016-05-13.
- ISBN 9781139473736.
- ISBN 0-07-072191-2
- ISBN 0-486-65812-0
- ^ Sidorov, L. A. (2001) [1994], "Angle", Encyclopedia of Mathematics, EMS Press
- ISBN 978-0-495-56521-5.
- MR 0006034.
External links
- "Line (curve)", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Equations of the Straight Line at Cut-the-Knot










































