Logic gate

A logic gate is a device that performs a
The primary way of building logic gates uses
Logic gates can be cascaded in the same way that Boolean functions can be composed, allowing the construction of a physical model of all of
Compound logic gates
History and development
The
In an 1886 letter,
From 1934 to 1936,
Symbols
There are two sets of symbols for elementary logic gates in common use, both defined in
The mutual goal of IEEE Std 91-1984 and IEC 617-12 was to provide a uniform method of describing the complex logic functions of digital circuits with schematic symbols. These functions were more complex than simple AND and OR gates. They could be medium-scale circuits such as a 4-bit counter to a large-scale circuit such as a microprocessor.
IEC 617-12 and its renumbered successor IEC 60617-12 do not explicitly show the "distinctive shape" symbols, but do not prohibit them.[16] These are, however, shown in ANSI/IEEE Std 91 (and 91a) with this note: "The distinctive-shape symbol is, according to IEC Publication 617, Part 12, not preferred, but is not considered to be in contradiction to that standard." IEC 60617-12 correspondingly contains the note (Section 2.1) "Although non-preferred, the use of other symbols recognized by official national standards, that is distinctive shapes in place of symbols [list of basic gates], shall not be considered to be in contradiction with this standard. Usage of these other symbols in combination to form complex symbols (for example, use as embedded symbols) is discouraged." This compromise was reached between the respective IEEE and IEC working groups to permit the IEEE and IEC standards to be in mutual compliance with one another.
In the 1980s, schematics were the predominant method to design both
| Type | Distinctive shape (IEEE Std 91/91a-1991) |
Rectangular shape (IEEE Std 91/91a-1991) (IEC 60617-12:1997) |
Boolean algebra between A and B | Truth table | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Single-input gates | ||||||||||||||||||||||
Buffer
|
| |||||||||||||||||||||
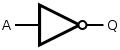
NOT (inverter) |
or |
| ||||||||||||||||||||
| In electronics a NOT gate is more commonly called an inverter. The circle on the symbol is called a bubble and is used in logic diagrams to indicate a logic negation between the external logic state and the internal logic state (1 to 0 or vice versa). On a circuit diagram it must be accompanied by a statement asserting that the positive logic convention or negative logic convention is being used (high voltage level = 1 or low voltage level = 1, respectively). The wedge is used in circuit diagrams to directly indicate an active-low (low voltage level = 1) input or output without requiring a uniform convention throughout the circuit diagram. This is called Direct Polarity Indication. See IEEE Std 91/91A and IEC 60617-12. Both the bubble and the wedge can be used on distinctive-shape and rectangular-shape symbols on circuit diagrams, depending on the logic convention used. On pure logic diagrams, only the bubble is meaningful. | ||||||||||||||||||||||
| Conjunction and disjunction | ||||||||||||||||||||||
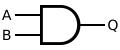
| AND | or |
| ||||||||||||||||||||
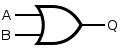
| OR | or |
| ||||||||||||||||||||
| Alternative denial and joint denial | ||||||||||||||||||||||
| NAND | or |
| ||||||||||||||||||||
| NOR | 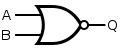
|

|
or |
| ||||||||||||||||||
| Exclusive or and biconditional | ||||||||||||||||||||||
| XOR | 
|

|
or |
| ||||||||||||||||||
| The output of a two input exclusive-OR is true only when the two input values are different, and false if they are equal, regardless of the value. If there are more than two inputs, the output of the distinctive-shape symbol is undefined. The output of the rectangular-shaped symbol is true if the number of true inputs is exactly one or exactly the number following the "=" in the qualifying symbol. | ||||||||||||||||||||||
| XNOR | 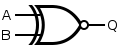
|
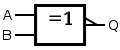
|
or |
| ||||||||||||||||||
De Morgan equivalent symbols
By use of De Morgan's laws, an AND function is identical to an OR function with negated inputs and outputs. Likewise, an OR function is identical to an AND function with negated inputs and outputs. A NAND gate is equivalent to an OR gate with negated inputs, and a NOR gate is equivalent to an AND gate with negated inputs.
This leads to an alternative set of symbols for basic gates that use the opposite core symbol (AND or OR) but with the inputs and outputs negated. Use of these alternative symbols can make logic circuit diagrams much clearer and help to show accidental connection of an active high output to an active low input or vice versa. Any connection that has logic negations at both ends can be replaced by a negationless connection and a suitable change of gate or vice versa. Any connection that has a negation at one end and no negation at the other can be made easier to interpret by instead using the De Morgan equivalent symbol at either of the two ends. When negation or polarity indicators on both ends of a connection match, there is no logic negation in that path (effectively, bubbles "cancel"), making it easier to follow logic states from one symbol to the next. This is commonly seen in real logic diagrams – thus the reader must not get into the habit of associating the shapes exclusively as OR or AND shapes, but also take into account the bubbles at both inputs and outputs in order to determine the "true" logic function indicated.
A De Morgan symbol can show more clearly a gate's primary logical purpose and the polarity of its nodes that are considered in the "signaled" (active, on) state. Consider the simplified case where a two-input NAND gate is used to drive a motor when either of its inputs are brought low by a switch. The "signaled" state (motor on) occurs when either one OR the other switch is on. Unlike a regular NAND symbol, which suggests AND logic, the De Morgan version, a two negative-input OR gate, correctly shows that OR is of interest. The regular NAND symbol has a bubble at the output and none at the inputs (the opposite of the states that will turn the motor on), but the De Morgan symbol shows both inputs and output in the polarity that will drive the motor.
De Morgan's theorem is most commonly used to implement logic gates as combinations of only NAND gates, or as combinations of only NOR gates, for economic reasons.
Truth tables
Output comparison of various logic gates:
| Input | Output | |
| A | Buffer | Inverter |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| Input | Output | ||||||
| A | B | AND | NAND | OR | NOR | XOR | XNOR |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
Universal logic gates
| type | NAND construction | NOR construction |
|---|---|---|
| NOT | 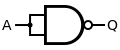
|
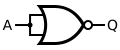
|
| AND | 
|
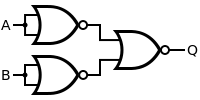
|
| NAND | 
|

|
| OR | 
|
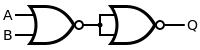
|
| NOR | 
|

|
| XOR | 
|

|
| XNOR | 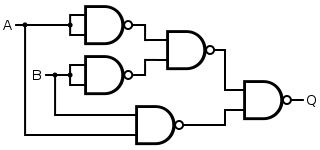
|

|
Data storage and sequential logic
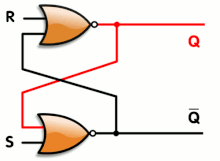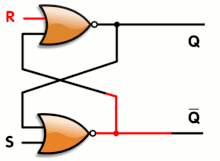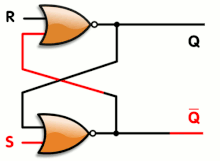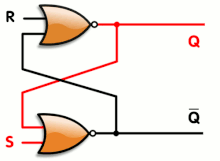
Logic gates can also be used to hold a state, allowing data storage. A storage element can be constructed by connecting several gates in a "
These logic circuits are used in computer memory. They vary in performance, based on factors of speed, complexity, and reliability of storage, and many different types of designs are used based on the application.
Manufacturing
Electronic gates
A
Electronic logic gates differ significantly from their relay-and-switch equivalents. They are much faster, consume much less power, and are much smaller (all by a factor of a million or more in most cases). Also, there is a fundamental structural difference. The switch circuit creates a continuous metallic path for current to flow (in either direction) between its input and its output. The semiconductor logic gate, on the other hand, acts as a high-

For small-scale logic, designers now use prefabricated logic gates from families of devices such as the
An important advantage of standardized integrated circuit logic families, such as the 7400 and 4000 families, is that they can be cascaded. This means that the output of one gate can be wired to the inputs of one or several other gates, and so on. Systems with varying degrees of complexity can be built without great concern of the designer for the internal workings of the gates, provided the limitations of each integrated circuit are considered.
The output of one gate can only drive a finite number of inputs to other gates, a number called the 'fan-out limit'. Also, there is always a delay, called the 'propagation delay', from a change in input of a gate to the corresponding change in its output. When gates are cascaded, the total propagation delay is approximately the sum of the individual delays, an effect which can become a problem in high-speed synchronous circuits. Additional delay can be caused when many inputs are connected to an output, due to the distributed capacitance of all the inputs and wiring and the finite amount of current that each output can provide.
Logic families
There are several logic families with different characteristics (power consumption, speed, cost, size) such as: RDL (resistor–diode logic), RTL (resistor-transistor logic), DTL (diode–transistor logic), TTL (transistor–transistor logic) and CMOS. There are also sub-variants, e.g. standard CMOS logic vs. advanced types using still CMOS technology, but with some optimizations for avoiding loss of speed due to slower PMOS transistors.
The simplest family of logic gates uses
As integrated circuits became more complex, bipolar transistors were replaced with smaller field-effect transistors (MOSFETs); see PMOS and NMOS. To reduce power consumption still further, most contemporary chip implementations of digital systems now use CMOS logic. CMOS uses complementary (both n-channel and p-channel) MOSFET devices to achieve a high speed with low power dissipation.
Other types of logic gates include, but are not limited to:[20]
| Logic family | Abbreviation | Description |
|---|---|---|
| Diode logic | DL | |
| Tunnel diode logic | TDL | Exactly the same as diode logic but can perform at a higher speed.[failed verification] |
| Neon logic | NL | Uses neon bulbs or 3-element neon trigger tubes to perform logic. |
| Core diode logic | CDL | Performed by semiconductor diodes and small ferrite toroidal cores for moderate speed and moderate power level. |
| 4Layer Device Logic | 4LDL | Uses thyristors and SCRs to perform logic operations where high current and or high voltages are required. |
| Direct-coupled transistor logic | DCTL | Uses transistors switching between saturated and cutoff states to perform logic. The transistors require carefully controlled parameters. Economical because few other components are needed, but tends to be susceptible to noise because of the lower voltage levels employed. Often considered to be the father to modern TTL logic. |
Metal–oxide–semiconductor logic |
MOS | Uses complementary MOS (CMOS), and BiCMOS (bipolar CMOS).
|
| Current-mode logic | CML | Uses transistors to perform logic but biasing is from constant current sources to prevent saturation and allow extremely fast switching. Has high noise immunity despite fairly low logic levels. |
| Quantum-dot cellular automata | QCA | Uses tunnelable q-bits for synthesizing the binary logic bits. The electrostatic repulsive force in between two electrons in the quantum dots assigns the electron configurations (that defines state 1 or state 0) under the suitably driven polarizations. This is a transistorless, currentless, junctionless binary logic synthesis technique allowing it to have very fast operation speeds. |
| Ferroelectric FET | FeFET | FeFET transistors can retain their state to speed recovery in case of a power loss.[21] |
Three-state logic gates
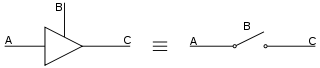
A three-state logic gate is a type of logic gate that can have three different outputs: high (H), low (L) and high-impedance (Z). The high-impedance state plays no role in the logic, which is strictly binary. These devices are used on
In electronics, a high output would mean the output is sourcing current from the positive power terminal (positive voltage). A low output would mean the output is sinking current to the negative power terminal (zero voltage). High impedance would mean that the output is effectively disconnected from the circuit.
Non-electronic logic gates
Non-electronic implementations are varied, though few of them are used in practical applications. Many early electromechanical digital computers, such as the
In principle any method that leads to a gate that is functionally complete (for example, either a NOR or a NAND gate) can be used to make any kind of digital logic circuit. Note that the use of 3-state logic for bus systems is not needed, and can be replaced by digital multiplexers, which can be built using only simple logic gates (such as NAND gates, NOR gates, or AND and OR gates).
See also
- And-inverter graph
- Boolean algebra topics
- Boolean function
- Depletion-load NMOS logic
- Digital circuit
- Espresso heuristic logic minimizer
- Emitter-coupled logic
- Fan-out
- Field-programmable gate array (FPGA)
- Flip-flop (electronics)
- Functional completeness
- Integrated injection logic
- Karnaugh map
- Combinational logic
- List of 4000 series integrated circuits
- List of 7400 series integrated circuits
- Logic family
- Logic level
- Logical graph
- NMOS logic
- Parametron
- Processor design
- Programmable logic controller (PLC)
- Programmable logic device (PLD)
- Propositional calculus
- Quantum logic gate
- Race hazard
- Reversible computing
- Superconducting computing
- Truth table
References
- ISBN 0-07-032482-4.
- ^ Kanellos, Michael (2003-02-11). "Moore's Law to roll on for another decade". CNET. From Integrated circuit
- ^ https://pubs.aip.org/aip/apl/article-abstract/106/11/113503/27163/Acoustic-logic-gates-and-Boolean-operation-based?redirectedFrom=fulltext
- S2CID 10934270.
- ISBN 0-12-691295-5.
- ISBN 978-0-300-08185-5. Retrieved 2010-06-08.
- ISBN 9780521830249.
... one of the traditional orderings of the hexagrams, the xiantian tu ordering made by Shao Yong, was, with a few modifications, the same order found in Leibniz's binary arithmetic.
- .
- .
- ^ "Switching Theory/Relay Circuit Network Theory/Theory of Logical Mathematics". IPSJ Computer Museum. Information Processing Society of Japan.
- CiteSeerX 10.1.1.66.1248.
- ^ ISSN 1456-2774. Archived from the original (PDF) on 2021-03-08.
{{cite book}}: CS1 maint: location missing publisher (link) (3+207+1 pages) 10:00 min - ISBN 978-3-54034258-8.
- ^ "1963: Complementary MOS Circuit Configuration is Invented". Computer History Museum. Retrieved 2019-07-06.
- ^ "Graphical Symbols for Logic Diagrams". ASSIST Quick Search. Defense Logistics Agency. MIL-STD-806. Retrieved 2021-08-27.
- ^ a b "Overview of IEEE Standard 91-1984 Explanation of Logic Symbols" (PDF). Texas Instruments Semiconductor Group. 1996. SDYZ001A.
- ISBN 978-3-11022622-5.
- ISBN 978-0-521-63017-7.
- ISBN 978-0-7506-8555-9.
- ^ Rowe, Jim. "Circuit Logic – Why and How". No. December 1966. Electronics Australia.
- ^ "Tapping into Non-Volatile Logic". 2021-04-21.
- Xerox PARC.
- PMID 29493684.
- PMID 11929243.
Further reading
- Awschalom, D. D.; Loss, D.; Samarth, N. (2002). Semiconductor Spintronics and Quantum Computation. Springer. ISBN 978-3-540-42176-4.
- Bostock, Geoff (1988). Programmable logic devices: technology and applications. ISBN 978-0-07-006611-3.
- Brown, Stephen D.; Francis, Robert J.; Rose, Jonathan; Vranesic, Zvonko G. (1992). Field Programmable Gate Arrays. ISBN 978-0-7923-9248-4.
External links
 Media related to Logic gates at Wikimedia Commons
Media related to Logic gates at Wikimedia Commons