Mathematical physics
| Part of a series on | ||
| Mathematics | ||
|---|---|---|
|
|
||
|
| ||
| Part of a series on |
| Physics |
|---|
 |
Mathematical physics refers to the development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines the field as "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and for the formulation of physical theories".[1] An alternative definition would also include those mathematics that are inspired by physics, known as physical mathematics.[2]
Scope
There are several distinct branches of mathematical physics, and these roughly correspond to particular historical parts of our world.
Classical mechanics
Applying the techniques of mathematical physics to classical mechanics typically involves the rigorous, abstract, and advanced reformulation of Newtonian mechanics in terms of Lagrangian mechanics and Hamiltonian mechanics (including both approaches in the presence of constraints). Both formulations are embodied in analytical mechanics and lead to an understanding of the deep interplay between the notions of symmetry and conserved quantities during the dynamical evolution of mechanical systems, as embodied within the most elementary formulation of Noether's theorem. These approaches and ideas have been extended to other areas of physics, such as statistical mechanics, continuum mechanics, classical field theory, and quantum field theory. Moreover, they have provided multiple examples and ideas in differential geometry (e.g., several notions in symplectic geometry and vector bundles).
Partial differential equations
Within mathematics proper, the theory of
.Quantum theory
The theory of
Relativity and quantum relativistic theories
The special and general theories of relativity require a rather different type of mathematics. This was group theory, which played an important role in both quantum field theory and differential geometry. This was, however, gradually supplemented by topology and functional analysis in the mathematical description of cosmological as well as quantum field theory phenomena. In the mathematical description of these physical areas, some concepts in homological algebra and category theory[3] are also important.
Statistical mechanics
Statistical mechanics forms a separate field, which includes the theory of phase transitions. It relies upon the Hamiltonian mechanics (or its quantum version) and it is closely related with the more mathematical ergodic theory and some parts of probability theory. There are increasing interactions between combinatorics and physics, in particular statistical physics.
Usage
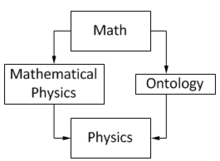
The usage of the term "mathematical physics" is sometimes
Mathematical vs. theoretical physics
The term "mathematical physics" is sometimes used to denote research aimed at studying and solving problems in physics or
On the other hand, theoretical physics emphasizes the links to observations and
Such mathematical physicists primarily expand and elucidate physical
The effort to put physical theories on a mathematically rigorous footing not only developed physics but also has influenced developments of some mathematical areas. For example, the development of quantum mechanics and some aspects of functional analysis parallel each other in many ways. The mathematical study of quantum mechanics, quantum field theory, and quantum statistical mechanics has motivated results in operator algebras. The attempt to construct a rigorous mathematical formulation of quantum field theory has also brought about some progress in fields such as representation theory.
Prominent mathematical physicists
Before Newton
There is a tradition of mathematical analysis of nature that goes back to the ancient Greeks; examples include
In the first decade of the 16th century, amateur astronomer
An enthusiastic atomist,
An older contemporary of Newton, Christiaan Huygens, was the first to idealize a physical problem by a set of parameters and the first to fully mathematize a mechanistic explanation of unobservable physical phenomena, and for these reasons Huygens is considered the first theoretical physicist and one of the founders of modern mathematical physics.[12][13]
Newtonian and post Newtonian
In this era, important concepts in
In the 18th century, the Swiss
Into the early 19th century, following mathematicians in France, Germany and England had contributed to mathematical physics. The French Pierre-Simon Laplace (1749–1827) made paramount contributions to mathematical astronomy, potential theory. Siméon Denis Poisson (1781–1840) worked in analytical mechanics and potential theory. In Germany, Carl Friedrich Gauss (1777–1855) made key contributions to the theoretical foundations of electricity, magnetism, mechanics, and fluid dynamics. In England, George Green (1793–1841) published An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism in 1828, which in addition to its significant contributions to mathematics made early progress towards laying down the mathematical foundations of electricity and magnetism.
A couple of decades ahead of Newton's publication of a particle theory of light, the Dutch
The English physicist
Relativistic
By the 1880s, there was a prominent paradox that an observer within Maxwell's electromagnetic field measured it at approximately constant speed, regardless of the observer's speed relative to other objects within the electromagnetic field. Thus, although the observer's speed was continually lost[
In 1887, experimentalists Michelson and Morley failed to detect aether drift, however. It was hypothesized that motion into the aether prompted aether's shortening, too, as modeled in the
Austrian theoretical physicist and philosopher
In 1908, Einstein's former mathematics professor
Quantum
Another revolutionary development of the 20th century was
List of prominent contributors to mathematical physics in the 20th century
Prominent contributors to the 20th century's mathematical physics include (ordered by birth date):
- William Thomson (Lord Kelvin)[1824–1907]
- Oliver Heaviside [1850–1925]
- Jules Henri Poincaré [1854–1912]
- David Hilbert [1862–1943]
- Arnold Sommerfeld [1868–1951]
- Constantin Carathéodory [1873–1950]
- Albert Einstein [1879–1955]
- Max Born [1882–1970]
- George David Birkhoff [1884–1944]
- Hermann Weyl [1885–1955]
- Satyendra Nath Bose [1894–1974]
- Norbert Wiener [1894–1964]
- John Lighton Synge [1897–1995]
- Mário Schenberg [1914–1990]
- Wolfgang Pauli [1900–1958]
- Paul Dirac [1902–1984]
- Eugene Wigner [1902–1995]
- Andrey Kolmogorov [1903–1987]
- Lars Onsager [1903–1976]
- John von Neumann [1903–1957]
- Sin-Itiro Tomonaga[1906–1979]
- Hideki Yukawa [1907–1981]
- Nikolay Nikolayevich Bogolyubov [1909–1992]
- Subrahmanyan Chandrasekhar [1910–1995]
- Mark Kac [1914–1984]
- Julian Schwinger [1918–1994]
- Richard Phillips Feynman [1918–1988]
- Irving Ezra Segal[1918–1998]
- Ryogo Kubo [1920–1995]
- Arthur Strong Wightman[1922–2013]
- Chen-Ning Yang[1922– ]
- Rudolf Haag [1922–2016]
- Freeman John Dyson [1923–2020]
- Martin Gutzwiller [1925–2014]
- Abdus Salam [1926–1996]
- Jürgen Moser [1928–1999]
- Michael Francis Atiyah [1929–2019]
- Joel Louis Lebowitz [1930– ]
- Roger Penrose [1931– ]
- Elliott Hershel Lieb [1932– ]
- Yakir Aharonov [1932– ]
- Sheldon Glashow [1932– ]
- Steven Weinberg [1933–2021]
- Ludvig Dmitrievich Faddeev [1934–2017]
- David Ruelle [1935– ]
- Yakov Grigorevich Sinai [1935– ]
- Vladimir Igorevich Arnold [1937–2010]
- Arthur Michael Jaffe [1937– ]
- Roman Wladimir Jackiw [1939– ]
- Leonard Susskind [1940– ]
- Rodney James Baxter [1940– ]
- Michael Victor Berry [1941– ]
- Giovanni Gallavotti [1941– ]
- Stephen William Hawking [1942–2018]
- Jerrold Eldon Marsden [1942–2010]
- Michael C. Reed [1942– ]
- John Michael Kosterlitz[1943– ]
- Israel Michael Sigal [1945– ]
- Alexander Markovich Polyakov [1945– ]
- Barry Simon [1946– ]
- Herbert Spohn [1946– ]
- John Lawrence Cardy [1947– ]
- Giorgio Parisi [1948- ]
- Abhay Ashtekar [1949- ]
- Edward Witten [1951– ]
- F. Duncan Haldane[1951– ]
- Ashoke Sen [1956– ]
- Juan Martín Maldacena[1968– ]
See also
- International Association of Mathematical Physics
- Notable publications in mathematical physics
- List of mathematical physics journals
- Gauge theory (mathematics)
- Relationship between mathematics and physics
- Theoretical, computational and philosophical physics
Notes
- ^ Definition from the Journal of Mathematical Physics. "Archived copy". Archived from the original on 2006-10-03. Retrieved 2006-10-03.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ "Physical mathematics and the future" (PDF). www.physics.rutgers.edu. Retrieved 2022-05-09.
- ^ "quantum field theory". nLab.
- ^ John Herapath (1847) Mathematical Physics; or, the Mathematical Principles of Natural Philosophy, the causes of heat, gaseous elasticity, gravitation, and other great phenomena of nature, Whittaker and company via HathiTrust
- ^ Quote: " ... a negative definition of the theorist refers to his inability to make physical experiments, while a positive one... implies his encyclopaedic knowledge of physics combined with possessing enough mathematical armament. Depending on the ratio of these two components, the theorist may be nearer either to the experimentalist or to the mathematician. In the latter case, he is usually considered as a specialist in mathematical physics.", Ya. Frenkel, as related in A.T. Filippov, The Versatile Soliton, pg 131. Birkhauser, 2000.
- ^ Quote: "Physical theory is something like a suit sewed for Nature. Good theory is like a good suit. ... Thus the theorist is like a tailor." Ya. Frenkel, as related in Filippov (2000), pg 131.
- ^ Pellegrin, P. (2000). Brunschwig, J.; Lloyd, G. E. R. (eds.). "Physics". Greek Thought: A Guide to Classical Knowledge: 433–451.
- ^ Berggren, J. L. (2008). "The Archimedes codex" (PDF). Notices of the AMS. 55 (8): 943–947.
- ^ Peter Machamer "Galileo Galilei"—sec 1 "Brief biography", in Zalta EN, ed, The Stanford Encyclopedia of Philosophy, Spring 2010 edn
- ^ a b Antony G Flew, Dictionary of Philosophy, rev 2nd edn (New York: St Martin's Press, 1984), p 129
- ^ Antony G Flew, Dictionary of Philosophy, rev 2nd edn (New York: St Martin's Press, 1984), p 89
- ^ Dijksterhuis, F. J. (2008). Stevin, Huygens and the Dutch republic. Nieuw archief voor wiskunde, 5, pp. 100–107. https://research.utwente.nl/files/6673130/Dijksterhuis_naw5-2008-09-2-100.pdf
- ^ Andreessen, C.D. (2005) Huygens: The Man Behind the Principle. Cambridge University Press: 6
- ^ Gregory, James (1668). Geometriae Pars Universalis. Museo Galileo: Patavii: typis heredum Pauli Frambotti.
- ^ "The Mathematical Principles of Natural Philosophy", Encyclopædia Britannica, London
- ^ a b Imre Lakatos, auth, Worrall J & Currie G, eds, The Methodology of Scientific Research Programmes: Volume 1: Philosophical Papers (Cambridge: Cambridge University Press, 1980), pp 213–214, 220
- ^ Minkowski, Hermann (1908–1909), "Raum und Zeit" [Space and Time], Physikalische Zeitschrift, 10: 75–88
- ^ Salmon WC & Wolters G, eds, Logic, Language, and the Structure of Scientific Theories (Pittsburgh: University of Pittsburgh Press, 1994), p 125
- ^
McCormmach, Russell (Spring 1967). "Henri Poincaré and the Quantum Theory". Isis. 58 (1): 37–55. S2CID 120934561.
- ^ Irons, F. E. (August 2001). "Poincaré's 1911–12 proof of quantum discontinuity interpreted as applying to atoms". American Journal of Physics. 69 (8): 879–84. .
References
- Bibcode:2005physics...6153Z
Further reading
Generic works
- Allen, Jont (2020), An Invitation to Mathematical Physics and its History, Springer, ISBN 978-3-030-53758-6
- Methods of Mathematical Physics, Vol 1–2, Interscience Publishers
- Françoise, Jean P.; Naber, Gregory L.; Tsun, Tsou S. (2006), Encyclopedia of Mathematical Physics, Elsevier, ISBN 978-0-1251-2660-1
- ISBN 0-486-65227-0
- ISBN 3-540-58661-X
- ISBN 978-1444627473
- Masani, Pesi R. (1976–1986), Norbert Wiener: Collected Works with Commentaries, Vol 1–4, The MIT Press
- ISBN 0-07-043316-X
- Thirring, Walter E. (1978–1983), A Course in Mathematical Physics, Vol 1–4, Springer-Verlag
- Tikhomirov, Vladimir M. (1991–1993), Selected Works of A. N. Kolmogorov, Vol 1–3, Kluwer Academic Publishers
- Titchmarsh, Edward C.(1985), The Theory of Functions (2nd ed.), Oxford University Press
Textbooks for undergraduate studies
- , archive.org)
- Bayın, Selçuk Ş. (2018), Mathematical Methods in Science and Engineering (2nd ed.), Wiley, ISBN 9781119425397
- ISBN 978-0-471-19826-0
- Butkov, Eugene (1968), Mathematical Physics, Addison-Wesley
- Hassani, Sadri (2009), Mathematical Methods for Students of Physics and Related Fields, (2nd ed.), New York, Springer, eISBN 978-0-387-09504-2
- Jeffreys, Harold; Swirles Jeffreys, Bertha (1956), Methods of Mathematical Physics (3rd ed.), Cambridge University Press
- Marsh, Adam (2018), Mathematics for Physics: An Illustrated Handbook, World Scientific, ISBN 978-981-3233-91-1
- ISBN 0-8053-7002-1
- ISBN 0-486-60056-4
- ISBN 978-0-521-86153-3
- ISBN 0-89871-456-7
- Starkovich, Steven P. (2021), The Structures of Mathematical Physics: An Introduction, Springer, ISBN 978-3-030-73448-0
Textbooks for graduate studies
- ISBN 978-3-319-14044-5
- Cahill, Kevin (2019), Physical Mathematics (2nd ed.), Cambridge University Press, ISBN 978-1-108-47003-2
- ISBN 0-226-28862-5
- Hassani, Sadri (2013), Mathematical Physics: A Modern Introduction to its Foundations (2nd ed.), Springer-Verlag, ISBN 978-3-319-01194-3
- Marathe, Kishore (2010), Topics in Physical Mathematics, Springer-Verlag, ISBN 978-1-84882-938-1
- Milstein, Grigori N.; Tretyakov, Michael V. (2021), Stochastic Numerics for Mathematical Physics (2nd ed.), Springer, ISBN 978-3-030-82039-8
- Reed, Michael C.; Simon, Barry (1972–1981), Methods of Modern Mathematical Physics, Vol 1-4, Academic Press
- Richtmyer, Robert D. (1978–1981), Principles of Advanced Mathematical Physics, Vol 1-2., Springer-Verlag
- Rudolph, Gerd; Schmidt, Matthias (2013–2017), Differential Geometry and Mathematical Physics, Vol 1-2, Springer
- Serov, Valery (2017), Fourier Series, Fourier Transform and Their Applications to Mathematical Physics, Springer, ISBN 978-3-319-65261-0
- Simon, Barry (2015), A Comprehensive Course in Analysis, Vol 1-5, American Mathematical Society
- ISBN 978-0-470-60970-5
- Stone, Michael; ISBN 978-0-521-85403-0
- Szekeres, Peter (2004), A Course in Modern Mathematical Physics: Groups, Hilbert Space and Differential Geometry, Cambridge University Press, ISBN 978-0-521-53645-5
- Taylor, Michael E. (2011), Partial Differential Equations, Vol 1-3 (2nd ed.), Springer.
- A Course of Modern Analysis: An Introduction to the General Theory of Infinite Processes and of Analytic Functions, with an Account of the Principal Transcendental Functions(4th ed.), Cambridge University Press
Specialized texts in classical physics
- ISBN 978-0-8218-4438-0
- Adam, John A. (2017), Rays, Waves, and Scattering: Topics in Classical Mathematical Physics, Princeton University Press., ISBN 978-0-691-14837-3
- ISBN 0-387-96890-3
- Bloom, Frederick (1993), Mathematical Problems of Classical Nonlinear Electromagnetic Theory, CRC Press, ISBN 0-582-21021-6
- Boyer, Franck; Fabrie, Pierre (2013), Mathematical Tools for the Study of the Incompressible Navier-Stokes Equations and Related Models, Springer, ISBN 978-1-4614-5974-3
- Colton, David; Kress, Rainer (2013), Integral Equation Methods in Scattering Theory, Society for Industrial and Applied Mathematics, ISBN 978-1-611973-15-0
- Ciarlet, Philippe G. (1988–2000), Mathematical Elasticity, Vol 1–3, Elsevier
- Galdi, Giovanni P. (2011), An Introduction to the Mathematical Theory of the Navier-Stokes Equations: Steady-State Problems (2nd ed.), Springer, ISBN 978-0-387-09619-3
- Hanson, George W.; Yakovlev, Alexander B. (2002), Operator Theory for Electromagnetics: An Introduction, Springer, ISBN 978-1-4419-2934-1
- Kirsch, Andreas; Hettlich, Frank (2015), The Mathematical Theory of Time-Harmonic Maxwell's Equations: Expansion-, Integral-, and Variational Methods, Springer, ISBN 978-3-319-11085-1
- Knauf, Andreas (2018), Mathematical Physics: Classical Mechanics, Springer, ISBN 978-3-662-55772-3
- Lechner, Kurt (2018), Classical Electrodynamics: A Modern Perspective, Springer, ISBN 978-3-319-91808-2
- ISBN 978-1-4419-3143-6
- Müller, Claus (1969), Foundations of the Mathematical Theory of Electromagnetic Waves, Springer-Verlag, ISBN 978-3-662-11775-0
- ISBN 9789813220966
- Roach, Gary F.; Stratis, Ioannis G.; Yannacopoulos, Athanasios N. (2012), Mathematical Analysis of Deterministic and Stochastic Problems in Complex Media Electromagnetics, Princeton University Press, ISBN 978-0-691-14217-3
Specialized texts in modern physics
- ISBN 981-02-2034-0
- Blank, Jiří; ISBN 978-1-4020-8869-8
- Engel, Eberhard; Dreizler, Reiner M. (2011), Density Functional Theory: An Advanced Course, Springer-Verlag, ISBN 978-3-642-14089-1
- ISBN 0-387-96477-0
- ISBN 3-540-61049-9
- Hall, Brian C. (2013), Quantum Theory for Mathematicians, Springer, ISBN 978-1-4614-7115-8
- Hamilton, Mark J. D. (2017), Mathematical Gauge Theory: With Applications to the Standard Model of Particle Physics, Springer, ISBN 978-3-319-68438-3
- ISBN 0-521-20016-4
- ISBN 9810216963
- Landsman, Klaas (2017), Foundations of Quantum Theory: From Classical Concepts to Operator Algebras, Springer, ISBN 978-3-319-51776-6
- Moretti, Valter (2017), Spectral Theory and Quantum Mechanics: Mathematical Foundations of Quantum Theories, Symmetries and Introduction to the Algebraic Formulation, Unitext, vol. 110 (2nd ed.), Springer, S2CID 125121522
- Robert, Didier; ISBN 978-3-030-70844-3
- Tasaki, Hal (2020), Physics and mathematics of quantum many-body systems, Springer, OCLC 1154567924
- ISBN 978-0-8218-4660-5
- ISBN 978-3-642-07711-1
- ISBN 978-0-691-17856-1
- ISBN 978-1614275800
- ISBN 978-3642069741
- Zeidler, Eberhard (2006–2011), Quantum Field Theory: A Bridge Between Mathematicians and Physicists, Vol 1-3, Springer
External links
 Media related to Mathematical physics at Wikimedia Commons
Media related to Mathematical physics at Wikimedia Commons
