Mathematics

Part of a series on
Mathematics
History Outline Index
Areas Number theory Geometry Algebra Calculus and Analysis Discrete mathematics Logic and Set theory Probability Statistics and Decision theory Relationship with sciences Physics Chemistry Geosciences Computation Biology Linguistics Economics Philosophy Education
Mathematics Portal
v t e

Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory,^[1] algebra,^[2] geometry,^[1] and analysis,^[3] respectively. There is no general consensus among mathematicians about a common definition for their academic discipline.

Most mathematical activity involves the discovery of properties of

Similarly, one of the two main schools of thought in Pythagoreanism was known as the mathēmatikoi (μαθηματικοί)—which at the time meant "learners" rather than "mathematicians" in the modern sense. The Pythagoreans were likely the first to constrain the use of the word to just the study of arithmetic and geometry. By the time of Aristotle (384–322 BC) this meaning was fully established.^[15]

In Latin, and in English until around 1700, the term mathematics more commonly meant "

Before the Renaissance, mathematics was divided into two main areas: arithmetic, regarding the manipulation of numbers, and geometry, regarding the study of shapes.^[20] Some types of pseudoscience, such as numerology and astrology, were not then clearly distinguished from mathematics.^[21]

During the Renaissance, two more areas appeared.

Number theory began with the manipulation of numbers, that is, natural numbers ${\displaystyle (\mathbb {N} ),}$ and later expanded to integers ${\displaystyle (\mathbb {Z} )}$ and rational numbers ${\displaystyle (\mathbb {Q} ).}$ Number theory was once called arithmetic, but nowadays this term is mostly used for

Geometry is one of the oldest branches of mathematics. It started with empirical recipes concerning shapes, such as lines, angles and circles, which were developed mainly for the needs of surveying and architecture, but has since blossomed out into many other subfields.^[33]

A fundamental innovation was the ancient Greeks' introduction of the concept of

Today's subareas of geometry include:[27]

• parallel lines
  intersect. This simplifies many aspects of classical geometry by unifying the treatments for intersecting and parallel lines.
• Affine geometry, the study of properties relative to parallelism and independent from the concept of length.
• Differential geometry, the study of curves, surfaces, and their generalizations, which are defined using differentiable functions.
• Manifold theory
  , the study of shapes that are not necessarily embedded in a larger space.
• Riemannian geometry, the study of distance properties in curved spaces.
• Algebraic geometry, the study of curves, surfaces, and their generalizations, which are defined using polynomials.
• continuous deformations
  .
  • Algebraic topology, the use in topology of algebraic methods, mainly homological algebra.
• Discrete geometry, the study of finite configurations in geometry.
• Convex geometry, the study of convex sets, which takes its importance from its applications in optimization.
• Complex geometry, the geometry obtained by replacing real numbers with complex numbers.

Algebra

Algebra is the art of manipulating

Algebra became an area in its own right only with

Until the 19th century, algebra consisted mainly of the study of

Some types of algebraic structures have useful and often fundamental properties, in many areas of mathematics. Their study became autonomous parts of algebra, and include:[27]

• group theory;
• field theory;
• vector spaces, whose study is essentially the same as linear algebra;
• ring theory;
• commutative algebra, which is the study of commutative rings, includes the study of polynomials, and is a foundational part of algebraic geometry;
• homological algebra;
• Lie algebra and Lie group theory;
• Boolean algebra, which is widely used for the study of the logical structure of computers.

The study of types of algebraic structures as mathematical objects is the purpose of universal algebra and category theory.^[46] The latter applies to every mathematical structure (not only algebraic ones). At its origin, it was introduced, together with homological algebra for allowing the algebraic study of non-algebraic objects such as topological spaces; this particular area of application is called algebraic topology.^[47]

Calculus and analysis

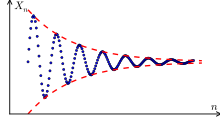
Calculus, formerly called infinitesimal calculus, was introduced independently and simultaneously by 17th-century mathematicians

Analysis is further subdivided into real analysis, where variables represent real numbers, and complex analysis, where variables represent complex numbers. Analysis includes many subareas shared by other areas of mathematics which include:^[27]

• Multivariable calculus
• Functional analysis, where variables represent varying functions;
• measure theory and potential theory, all strongly related with probability theory on a continuum
  ;
• Ordinary differential equations;
• Partial differential equations;
• Numerical analysis, mainly devoted to the computation on computers of solutions of ordinary and partial differential equations that arise in many applications.

Discrete mathematics

Discrete mathematics, broadly speaking, is the study of individual, countable mathematical objects. An example is the set of all integers.^[50] Because the objects of study here are discrete, the methods of calculus and mathematical analysis do not directly apply.^[d] Algorithms—especially their implementation and computational complexity—play a major role in discrete mathematics.^[51]

The

Discrete mathematics includes:[27]

• geometric shapes
• Graph theory and hypergraphs
• error correcting codes and a part of cryptography
• Matroid theory
• Discrete geometry
• Discrete probability distributions
• Game theory (although continuous games are also studied, most common games, such as chess and poker are discrete)
• Discrete optimization, including combinatorial optimization, integer programming, constraint programming

Mathematical logic and set theory

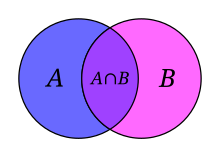
The two subjects of mathematical logic and set theory have belonged to mathematics since the end of the 19th century.^[54][55] Before this period, sets were not considered to be mathematical objects, and logic, although used for mathematical proofs, belonged to philosophy and was not specifically studied by mathematicians.^[56]

Before

The "nature" of the objects defined this way is a philosophical problem that mathematicians leave to philosophers, even if many mathematicians have opinions on this nature, and use their opinion—sometimes called "intuition"—to guide their study and proofs. The approach allows considering "logics" (that is, sets of allowed deducing rules), theorems, proofs, etc. as mathematical objects, and to prove theorems about them. For example, Gödel's incompleteness theorems assert, roughly speaking that, in every consistent formal system that contains the natural numbers, there are theorems that are true (that is provable in a stronger system), but not provable inside the system.^[62] This approach to the foundations of mathematics was challenged during the first half of the 20th century by mathematicians led by Brouwer, who promoted intuitionistic logic, which explicitly lacks the law of excluded middle.^[63][64]

These problems and debates led to a wide expansion of mathematical logic, with subareas such as model theory (modeling some logical theories inside other theories), proof theory, type theory, computability theory and computational complexity theory.^[27] Although these aspects of mathematical logic were introduced before the rise of computers, their use in compiler design, program certification, proof assistants and other aspects of computer science, contributed in turn to the expansion of these logical theories.^[65]

Statistics and other decision sciences

Computational mathematics is the study of

History

Ancient

The history of mathematics is an ever-growing series of abstractions. Evolutionarily speaking, the first abstraction to ever be discovered, one shared by many animals,

Evidence for more complex mathematics does not appear until around 3000 BC, when the Babylonians and Egyptians began using arithmetic, algebra, and geometry for taxation and other financial calculations, for building and construction, and for astronomy.^[76] The oldest mathematical texts from Mesopotamia and Egypt are from 2000 to 1800 BC. Many early texts mention Pythagorean triples and so, by inference, the Pythagorean theorem seems to be the most ancient and widespread mathematical concept after basic arithmetic and geometry. It is in Babylonian mathematics that elementary arithmetic (addition, subtraction, multiplication, and division) first appear in the archaeological record. The Babylonians also possessed a place-value system and used a sexagesimal numeral system which is still in use today for measuring angles and time.^[77]

In the 6th century BC, Greek mathematics began to emerge as a distinct discipline and some

The

During the

During the early modern period, mathematics began to develop at an accelerating pace in Western Europe, with innovations that revolutionized mathematics, such as the introduction of variables and symbolic notation by François Viète (1540–1603), the introduction of logarithms by John Napier in 1614, which greatly simplified numerical calculations, especially for astronomy and marine navigation, the introduction of coordinates by René Descartes (1596–1650) for reducing geometry to algebra, and the development of calculus by Isaac Newton (1642–1726/27) and Gottfried Leibniz (1646–1716). Leonhard Euler (1707–1783), the most notable mathematician of the 18th century, unified these innovations into a single corpus with a standardized terminology, and completed them with the discovery and the proof of numerous theorems.

Perhaps the foremost mathematician of the 19th century was the German mathematician Carl Gauss, who made numerous contributions to fields such as algebra, analysis,

Mathematics has since been greatly extended, and there has been a fruitful interaction between mathematics and science, to the benefit of both. Mathematical discoveries continue to be made to this very day. According to Mikhail B. Sevryuk, in the January 2006 issue of the Bulletin of the American Mathematical Society, "The number of papers and books included in the Mathematical Reviews database since 1940 (the first year of operation of MR) is now more than 1.9 million, and more than 75 thousand items are added to the database each year. The overwhelming majority of works in this ocean contain new mathematical theorems and their proofs."^[93]

Symbolic notation and terminology

Mathematical notation is widely used in science and

), ${\textstyle \int }$ (

Numerous technical terms used in mathematics are neologisms, such as polynomial and homeomorphism.^[99] Other technical terms are words of the common language that are used in an accurate meaning that may differ slightly from their common meaning. For example, in mathematics, "or" means "one, the other or both", while, in common language, it is either ambiguous or means "one or the other but not both" (in mathematics, the latter is called "exclusive or"). Finally, many mathematical terms are common words that are used with a completely different meaning.^[100] This may lead to sentences that are correct and true mathematical assertions, but appear to be nonsense to people who do not have the required background. For example, "every free module is flat" and "a field is always a ring".

Relationship with sciences

Mathematics is used in most

Isaac Newton (left) and Gottfried Wilhelm Leibniz developed infinitesimal calculus.

Until the 19th century, the development of mathematics in the West was mainly motivated by the needs of

In the 19th century, mathematicians such as Karl Weierstrass and Richard Dedekind increasingly focused their research on internal problems, that is, pure mathematics.^[111][115] This led to split mathematics into pure mathematics and applied mathematics, the latter being often considered as having a lower value among mathematical purists. However, the lines between the two are frequently blurred.^[116]

The aftermath of World War II led to a surge in the development of applied mathematics in the US and elsewhere.^[117][118] Many of the theories developed for applications were found interesting from the point of view of pure mathematics, and many results of pure mathematics were shown to have applications outside mathematics; in turn, the study of these applications may give new insights on the "pure theory".^[119][120]

An example of the first case is the

In the present day, the distinction between pure and applied mathematics is more a question of personal research aim of mathematicians than a division of mathematics into broad areas.[124]^[125] The Mathematics Subject Classification has a section for "general applied mathematics" but does not mention "pure mathematics".^[27] However, these terms are still used in names of some university departments, such as at the Faculty of Mathematics at the University of Cambridge.

Unreasonable effectiveness

The unreasonable effectiveness of mathematics is a phenomenon that was named and first made explicit by physicist Eugene Wigner.^[6] It is the fact that many mathematical theories (even the "purest") have applications outside their initial object. These applications may be completely outside their initial area of mathematics, and may concern physical phenomena that were completely unknown when the mathematical theory was introduced.^[126] Examples of unexpected applications of mathematical theories can be found in many areas of mathematics.

A notable example is the

In the 19th century, the internal development of geometry (pure mathematics) led to definition and study of non-Euclidean geometries, spaces of dimension higher than three and manifolds. At this time, these concepts seemed totally disconnected from the physical reality, but at the beginning of the 20th century, Albert Einstein developed the theory of relativity that uses fundamentally these concepts. In particular, spacetime of special relativity is a non-Euclidean space of dimension four, and spacetime of general relativity is a (curved) manifold of dimension four.^[129][130]

A striking aspect of the interaction between mathematics and physics is when mathematics drives research in physics. This is illustrated by the discoveries of the positron and the baryon ${\displaystyle \Omega ^{-}.}$ In both cases, the equations of the theories had unexplained solutions, which led to conjecture of the existence of an unknown particle, and the search for these particles. In both cases, these particles were discovered a few years later by specific experiments.^{[131][132][133]}

Specific sciences

This subsection is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. Please help improve it by rewriting it in an encyclopedic style. (December 2022) (Learn how and when to remove this template message)

Physics

Mathematics and physics have influenced each other over their modern history. Modern physics uses mathematics abundantly,^[134] and is also the motivation of major mathematical developments.^[135]

Computing

The rise of technology in the 20th century opened the way to a new science: computing.^[f] This field is closely related to mathematics in several ways. Theoretical computer science is essentially mathematical in nature. Communication technologies apply branches of mathematics that may be very old (e.g., arithmetic), especially with respect to transmission security, in cryptography and coding theory. Discrete mathematics is useful in many areas of computer science, such as complexity theory, information theory, graph theory, and so on.^{[citation needed]}

In return, computing has also become essential for obtaining new results. This is a group of techniques known as experimental mathematics, which is the use of experimentation to discover mathematical insights.^[136] The most well-known example is the four-color theorem, which was proven in 1976 with the help of a computer. This revolutionized traditional mathematics, where the rule was that the mathematician should verify each part of the proof. In 1998, the Kepler conjecture on sphere packing seemed to also be partially proven by computer. An international team had since worked on writing a formal proof; it was finished (and verified) in 2015.^[137]

Once written formally, a proof can be verified using a program called a proof assistant.^[138] These programs are useful in situations where one is uncertain about a proof's correctness.^[138]

A major open problem in theoretical computer science is P versus NP. It is one of the seven Millennium Prize Problems.^[139]

Biology and chemistry

Phylogeography uses probabilistic models.^{[citation needed]}

Medicine uses

Areas of mathematics used in the social sciences include probability/statistics and differential equations. These are used in linguistics, economics, sociology,^[146] and psychology.^[147]

The fundamental postulate of mathematical economics is that of the rational individual actor –

Creativity and rigor are not the only psychological aspects of the activity of mathematicians. Some mathematicians can see their activity as a game, more specifically as solving puzzles.^[184] This aspect of mathematical activity is emphasized in recreational mathematics.

Mathematicians can find an

The popularity of recreational mathematics is another sign of the pleasure many find in solving mathematical questions.

Cultural impact

The examples and perspective in this section deal primarily with Western culture and do not represent a worldwide view of the subject. You may improve this section, discuss the issue on the talk page, or create a new section, as appropriate. (December 2022) (Learn how and when to remove this template message)

Artistic expression

Notes that sound well together to a Western ear are sounds whose fundamental

multiplies it by ${\displaystyle {\frac {3}{2}}}$.

Humans, as well as some other animals, find symmetric patterns to be more beautiful.^[190] Mathematically, the symmetries of an object form a group known as the symmetry group.^[191]

For example, the group underlying mirror symmetry is the cyclic group of two elements, ${\displaystyle \mathbb {Z} /2\mathbb {Z} }$. A

Popular mathematics is the act of presenting mathematics without technical terms.^[196] Presenting mathematics may be hard since the general public suffers from mathematical anxiety and mathematical objects are highly abstract.^[197] However, popular mathematics writing can overcome this by using applications or cultural links.^[198] Despite this, mathematics is rarely the topic of popularization in printed or televised media.

Awards and prize problems

The most prestigious award in mathematics is the Fields Medal,^[199][200] established in 1936 and awarded every four years (except around World War II) to up to four individuals.^[201][202] It is considered the mathematical equivalent of the Nobel Prize.^[202]

Other prestigious mathematics awards include:^[203]

• The Abel Prize, instituted in 2002^[204] and first awarded in 2003^[205]
• The Chern Medal for lifetime achievement, introduced in 2009^[206] and first awarded in 2010^[207]
• The AMS Leroy P. Steele Prize, awarded since 1970^[208]
• The Wolf Prize in Mathematics, also for lifetime achievement,^[209] instituted in 1978^[210]

A famous list of 23 open problems, called "Hilbert's problems", was compiled in 1900 by German mathematician David Hilbert.^[211] This list has achieved great celebrity among mathematicians,^[212] and, as of 2022^[update], at least thirteen of the problems (depending how some are interpreted) have been solved.^[211]

A new list of seven important problems, titled the "Millennium Prize Problems", was published in 2000. Only one of them, the Riemann hypothesis, duplicates one of Hilbert's problems. A solution to any of these problems carries a 1 million dollar reward.^[213] To date, only one of these problems, the Poincaré conjecture, has been solved.^[214]

See also

References

Notes