Euclidean plane

The idea of this system was developed in 1637 in writings by Descartes and independently by

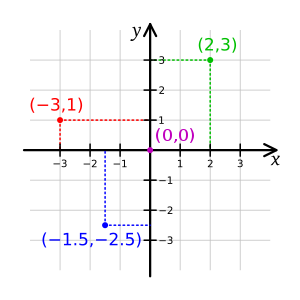
Coordinate systems

Another widely used coordinate system is the polar coordinate system, which specifies a point in terms of its distance from the origin and its angle relative to a rightward reference ray.

• 
  Cartesian coordinate system
• 
  Polar coordinate system

Embedding in three-dimensional space

This section is an excerpt from Euclidean planes in three-dimensional space.[edit]

In

surface

that extends indefinitely. Euclidean planes often arise as

subspaces of three-dimensional space

${\displaystyle \mathbb {R} ^{3}}$. A prototypical example is one of a room's walls, infinitely extended and assumed infinitesimal thin.

While a pair of real numbers ${\displaystyle \mathbb {R} ^{2}}$ suffices to describe points on a plane, the relationship with out-of-plane points requires special consideration for their

ambient space

${\displaystyle \mathbb {R} ^{3}}$.

In two dimensions, there are infinitely many polytopes: the polygons. The first few regular ones are shown below:

Convex

The Schläfli symbol ${\displaystyle \{n\}}$ represents a regular n-gon.

Name	Triangle (2-simplex)	Square (2-orthoplex) (2-cube )	Pentagon	Hexagon	Heptagon	Octagon
Schläfli symbol	{3}	{4}	{5}	{6}	{7}	{8}
Image
Name	Nonagon	Decagon	Hendecagon	Dodecagon	Tridecagon	Tetradecagon
Schläfli	{9}	{10}	{11}	{12}	{13}	{14}
Image
Name	Pentadecagon	Hexadecagon	Heptadecagon	Octadecagon	Enneadecagon	Icosagon	...n-gon
Schläfli	{15}	{16}	{17}	{18}	{19}	{20}	{n}
Image

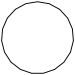
Degenerate (spherical)

The regular monogon (or henagon) {1} and regular digon {2} can be considered degenerate regular polygons and exist nondegenerately in non-Euclidean spaces like a 2-sphere, 2-torus, or right circular cylinder.

Name	Monogon	Digon
Schläfli	{1}	{2}
Image

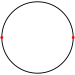
Non-convex

There exist infinitely many non-convex regular polytopes in two dimensions, whose Schläfli symbols consist of rational numbers {n/m}. They are called star polygons and share the same vertex arrangements of the convex regular polygons.

In general, for any natural number n, there are n-pointed non-convex regular polygonal stars with Schläfli symbols {n/m} for all m such that m < n/2 (strictly speaking {n/m} = {n/(n − m)}) and m and n are

Name	Pentagram	Heptagrams		Octagram	Enneagrams		Decagram	...n-agrams
Schläfli	{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}	{10/3}	{n/m}
Image

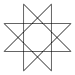
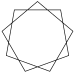
Circle

The

There are an infinitude of other curved shapes in two dimensions, notably including the conic sections: the ellipse, the parabola, and the hyperbola.

In linear algebra

Another mathematical way of viewing two-dimensional space is found in linear algebra, where the idea of independence is crucial. The plane has two dimensions because the length of a rectangle is independent of its width. In the technical language of linear algebra, the plane is two-dimensional because every point in the plane can be described by a linear combination of two independent vectors.

Dot product, angle, and length

The dot product of two vectors A = [A₁, A₂] and B = [B₁, B₂] is defined as:^[5]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =A_{1}B_{1}+A_{2}B_{2}}$

A vector can be pictured as an arrow. Its magnitude is its length, and its direction is the direction the arrow points. The magnitude of a vector A is denoted by ${\displaystyle \|\mathbf {A} \|}$. In this viewpoint, the dot product of two Euclidean vectors A and B is defined by^[6]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta ,}$

where θ is the angle between A and B.

The dot product of a vector A by itself is

${\displaystyle \mathbf {A} \cdot \mathbf {A} =\|\mathbf {A} \|^{2},}$

which gives

${\displaystyle \|\mathbf {A} \|={\sqrt {\mathbf {A} \cdot \mathbf {A} }},}$

the formula for the

In calculus

Gradient

In a rectangular coordinate system, the gradient is given by

${\displaystyle \nabla f={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} \,.}$

Line integrals and double integrals

For some

of the curve C such that r(a) and r(b) give the endpoints of C and ${\displaystyle a<b}$.

For a

${\displaystyle f(x,y),}$ and is usually written as:

${\displaystyle \iint \limits _{D}f(x,y)\,dx\,dy.}$

Fundamental theorem of line integrals

Main article:

Fundamental theorem of line integrals

The

Let C be a positively

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other.^[9] Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

See also

• Geometric space
• Picture function
• Planimetrics

References