Set theory

Part of a series on
Mathematics
History Index
Areas Number theory Geometry Algebra Calculus and Analysis Discrete mathematics Logic Set theory Probability Statistics and Decision theory Relationship with sciences Physics Chemistry Geosciences Computation Biology Linguistics Economics Philosophy Education
Mathematics Portal
v t e

Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory – as a branch of mathematics – is mostly concerned with those that are relevant to mathematics as a whole.

The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized systems investigated during this early stage go under the name of naive set theory. After the discovery of paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox), various axiomatic systems were proposed in the early twentieth century, of which Zermelo–Fraenkel set theory (with or without the axiom of choice) is still the best-known and most studied.

Set theory is commonly employed as a foundational system for the whole of mathematics, particularly in the form of Zermelo–Fraenkel set theory with the axiom of choice. Besides its foundational role, set theory also provides the framework to develop a mathematical theory of

The basic notion of grouping objects has existed since at least the

${\displaystyle [0,5]}$ and ${\displaystyle [0,12]}$ by the relation ${\displaystyle 5y=12x}$. However, he resisted saying these sets were

Set theory, as understood by modern mathematicians, is generally considered to be founded by a single paper in 1874 by

, which extended the arithmetic of the natural numbers. His notation for the cardinal numbers was the Hebrew letter ${\displaystyle \aleph }$ (

) with a natural number subscript; for the ordinals he employed the Greek letter ${\displaystyle \omega }$ (ω,

Set theory was beginning to become an essential ingredient of the new “modern” approach to mathematics. Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as

Despite the controversy, Cantor's set theory gained remarkable ground around the turn of the 20th century with the work of several notable mathematicians and philosophers. Richard Dedekind, around the same time, began working with sets in his publications, and famously constructing the real numbers using

In his work, Frege tries to ground all mathematics in terms of logical axioms using Cantor's cardinality. For example, the sentence "the number of horses in the barn is four" means that four objects fall under the concept horse in the barn. Frege attempted to explain our grasp of numbers through cardinality ('the number of...', or ${\displaystyle Nx:Fx}$), relying on Hume's principle.

However, Frege's work was short-lived, as it was found by

Set theory begins with a fundamental

Since sets are objects, the membership relation can relate sets as well, i.e., sets themselves can be members of other sets.

A derived binary relation between two sets is the subset relation, also called set inclusion. If all the members of set A are also members of set B, then A is a

proper subset

is defined, variously denoted ${\displaystyle A\subset B}$, ${\displaystyle A\subsetneq B}$, or ${\displaystyle A\subsetneqq B}$ (note however that the notation ${\displaystyle A\subset B}$ is sometimes used synonymously with ${\displaystyle A\subseteq B}$; that is, allowing the possibility that A and B are equal). We call A a proper subset of B if and only if A is a subset of B, but A is not equal to B. Also, 1, 2, and 3 are members (elements) of the set {1, 2, 3}, but are not subsets of it; and in turn, the subsets, such as {1}, are not members of the set {1, 2, 3}. More complicated relations can exist; for example, the set {1} is both a member and a proper subset of the set {1, {1}}.

Just as arithmetic features binary operations on numbers, set theory features binary operations on sets.^[9] The following is a partial list of them:

• Union of the sets A and B, denoted A ∪ B, is the set of all objects that are a member of A, or B, or both.^[10] For example, the union of {1, 2, 3} and {2, 3, 4} is the set {1, 2, 3, 4}.
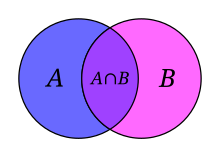
• Intersection of the sets A and B, denoted A ∩ B, is the set of all objects that are members of both A and B.^[11] For example, the intersection of {1, 2, 3} and {2, 3, 4} is the set {2, 3}.
• Set difference of U and A, denoted U ∖ A, is the set of all members of U that are not members of A.^[12] The set difference {1, 2, 3} ∖ {2, 3, 4} is {1}, while conversely, the set difference {2, 3, 4} ∖ {1, 2, 3} is {4}. When A is a subset of U, the set difference U ∖ A is also called the complement of A in U. In this case, if the choice of U is clear from the context, the notation A^c is sometimes used instead of U ∖ A, particularly if U is a universal set as in the study of Venn diagrams.^[13]
• Symmetric difference of sets A and B, denoted A △ B or A ⊖ B, is the set of all objects that are a member of exactly one of A and B (elements which are in one of the sets, but not in both). For instance, for the sets {1, 2, 3} and {2, 3, 4}, the symmetric difference set is {1, 4}. It is the set difference of the union and the intersection, (A ∪ B) ∖ (A ∩ B) or (A ∖ B) ∪ (B ∖ A).
• Cartesian product of A and B, denoted A × B, is the set whose members are all possible ordered pairs (a, b), where a is a member of A and b is a member of B. For example, the Cartesian product of {1, 2} and {red, white} is {(1, red), (1, white), (2, red), (2, white)}.^[14]

Some basic sets of central importance are the set of natural numbers, the set of real numbers and the empty set – the unique set containing no elements. The empty set is also occasionally called the null set,^[15] though this name is ambiguous and can lead to several interpretations. The empty set can be denoted with empty braces "${\displaystyle \{\}}$" or the symbol "${\displaystyle \varnothing }$" or "${\displaystyle \emptyset }$".

The power set of a set A, denoted ${\displaystyle {\mathcal {P}}(A)}$, is the set whose members are all of the possible subsets of A. For example, the power set of {1, 2} is { {}, {1}, {2}, {1, 2} }. Notably, ${\displaystyle {\mathcal {P}}(A)}$ contains both A and the empty set.

A set is

${\displaystyle \alpha }$, known as its rank. The rank of a pure set ${\displaystyle X}$ is defined to be the least ordinal that is strictly greater than the rank of any of its elements. For example, the empty set is assigned rank 0, while the set containing only the empty set is assigned rank 1. For each ordinal ${\displaystyle \alpha }$, the set ${\displaystyle V_{\alpha }}$ is defined to consist of all pure sets with rank less than ${\displaystyle \alpha }$. The entire von Neumann universe is denoted ${\displaystyle V}$.

Formalized set theory

Elementary set theory can be studied informally and intuitively, and so can be taught in primary schools using Venn diagrams. The intuitive approach tacitly assumes that a set may be formed from the class of all objects satisfying any particular defining condition. This assumption gives rise to paradoxes, the simplest and best known of which are Russell's paradox and the Burali-Forti paradox. Axiomatic set theory was originally devised to rid set theory of such paradoxes.^{[note 1]}

The most widely studied systems of axiomatic set theory imply that all sets form a cumulative hierarchy.^[b] Such systems come in two flavors, those whose ontology consists of:

• Sets alone. This includes the most common axiomatic set theory, Zermelo–Fraenkel set theory with the axiom of choice (ZFC). Fragments of ZFC include:
  • separation
    ;
  • General set theory, a small fragment of Zermelo set theory sufficient for the Peano axioms and finite sets;
  • separation and replacement
    .
• Sets and
  ZFC for theorems about sets alone, and Morse–Kelley set theory and Tarski–Grothendieck set theory
  , both of which are stronger than ZFC.

The above systems can be modified to allow urelements, objects that can be members of sets but that are not themselves sets and do not have any members.

The New Foundations systems of NFU (allowing urelements) and NF (lacking them), associate with Willard Van Orman Quine, are not based on a cumulative hierarchy. NF and NFU include a "set of everything", relative to which every set has a complement. In these systems urelements matter, because NF, but not NFU, produces sets for which the axiom of choice does not hold. Despite NF's ontology not reflecting the traditional cumulative hierarchy and violating well-foundedness, Thomas Forster has argued that it does reflect an iterative conception of set.^[16]

Systems of

ZFC

are a related subject.

An enrichment of ZFC called internal set theory was proposed by Edward Nelson in 1977.^[17]

Applications

Many mathematical concepts can be defined precisely using only set theoretic concepts. For example, mathematical structures as diverse as

order relations are ubiquitous in mathematics, and the theory of mathematical relations can be described in set theory.^[18][19]

Set theory is also a promising foundational system for much of mathematics. Since the publication of the first volume of Principia Mathematica, it has been claimed that most (or even all) mathematical theorems can be derived using an aptly designed set of axioms for set theory, augmented with many definitions, using first or second-order logic. For example, properties of the natural and real numbers can be derived within set theory, as each of these number systems can be defined by representing their elements as sets of specific forms.^[20]

Set theory as a foundation for

propositional logic.^[21]

Areas of study

Set theory is a major area of research in mathematics with many interrelated subfields:

Combinatorial set theory

Main article: Infinitary combinatorics

Combinatorial set theory concerns extensions of finite

cardinal arithmetic and the study of extensions of Ramsey's theorem such as the Erdős–Rado theorem

.

Descriptive set theory

Main article: Descriptive set theory

Descriptive set theory is the study of subsets of the

real line and, more generally, subsets of Polish spaces. It begins with the study of pointclasses in the Borel hierarchy and extends to the study of more complex hierarchies such as the projective hierarchy and the Wadge hierarchy. Many properties of Borel sets

can be established in ZFC, but proving these properties hold for more complicated sets requires additional axioms related to determinacy and large cardinals.

The field of

lightface pointclasses, and is closely related to hyperarithmetical theory

. In many cases, results of classical descriptive set theory have effective versions; in some cases, new results are obtained by proving the effective version first and then extending ("relativizing") it to make it more broadly applicable.

A recent area of research concerns Borel equivalence relations and more complicated definable equivalence relations. This has important applications to the study of invariants in many fields of mathematics.

Fuzzy set theory

Main article:

Fuzzy set theory

In set theory as Cantor defined and Zermelo and Fraenkel axiomatized, an object is either a member of a set or not. In

fuzzy set theory this condition was relaxed by Lotfi A. Zadeh

so an object has a degree of membership in a set, a number between 0 and 1. For example, the degree of membership of a person in the set of "tall people" is more flexible than a simple yes or no answer and can be a real number such as 0.75.

Inner model theory

Main article: Inner model theory

An inner model of Zermelo–Fraenkel set theory (ZF) is a transitive

class that includes all the ordinals and satisfies all the axioms of ZF. The canonical example is the constructible universe

L developed by Gödel. One reason that the study of inner models is of interest is that it can be used to prove consistency results. For example, it can be shown that regardless of whether a model V of ZF satisfies the continuum hypothesis or the axiom of choice, the inner model L constructed inside the original model will satisfy both the generalized continuum hypothesis and the axiom of choice. Thus the assumption that ZF is consistent (has at least one model) implies that ZF together with these two principles is consistent.

The study of inner models is common in the study of determinacy and large cardinals, especially when considering axioms such as the axiom of determinacy that contradict the axiom of choice. Even if a fixed model of set theory satisfies the axiom of choice, it is possible for an inner model to fail to satisfy the axiom of choice. For example, the existence of sufficiently large cardinals implies that there is an inner model satisfying the axiom of determinacy (and thus not satisfying the axiom of choice).^[22]

Large cardinals

Main article:

Large cardinal property

A large cardinal is a cardinal number with an extra property. Many such properties are studied, including inaccessible cardinals, measurable cardinals, and many more. These properties typically imply the cardinal number must be very large, with the existence of a cardinal with the specified property unprovable in Zermelo–Fraenkel set theory.

Determinacy

Main article: Determinacy

Determinacy refers to the fact that, under appropriate assumptions, certain two-player games of perfect information are determined from the start in the sense that one player must have a winning strategy. The existence of these strategies has important consequences in descriptive set theory, as the assumption that a broader class of games is determined often implies that a broader class of sets will have a topological property. The

Wadge degrees

have an elegant structure.

Forcing

Main article: Forcing (mathematics)

relative consistency by finitistic methods, the other method being Boolean-valued models

.

Cardinal invariants

Main article:

Cardinal characteristics of the continuum

A cardinal invariant is a property of the real line measured by a cardinal number. For example, a well-studied invariant is the smallest cardinality of a collection of meagre sets of reals whose union is the entire real line. These are invariants in the sense that any two isomorphic models of set theory must give the same cardinal for each invariant. Many cardinal invariants have been studied, and the relationships between them are often complex and related to axioms of set theory.

Set-theoretic topology

Main article: Set-theoretic topology

Set-theoretic topology studies questions of general topology that are set-theoretic in nature or that require advanced methods of set theory for their solution. Many of these theorems are independent of ZFC, requiring stronger axioms for their proof. A famous problem is the normal Moore space question, a question in general topology that was the subject of intense research. The answer to the normal Moore space question was eventually proved to be independent of ZFC.

Controversy

Main article: Controversy over Cantor's theory

From set theory's inception, some mathematicians have objected to it as a

constructivist view that mathematics is loosely related to computation. If this view is granted, then the treatment of infinite sets, both in naive and in axiomatic set theory, introduces into mathematics methods and objects that are not computable even in principle. The feasibility of constructivism as a substitute foundation for mathematics was greatly increased by Errett Bishop's influential book Foundations of Constructive Analysis.^[23]

A different objection put forth by Henri Poincaré is that defining sets using the axiom schemas of specification and replacement, as well as the axiom of power set, introduces impredicativity, a type of circularity, into the definitions of mathematical objects. The scope of predicatively founded mathematics, while less than that of the commonly accepted Zermelo–Fraenkel theory, is much greater than that of constructive mathematics, to the point that Solomon Feferman has said that "all of scientifically applicable analysis can be developed [using predicative methods]".^[24]

Goodstein all pointed out, many of his critiques did not apply to the paper in full. Only recently have philosophers such as Crispin Wright begun to rehabilitate Wittgenstein's arguments.^[30]

computable set theory.^[31][32] Topoi also give a natural setting for forcing and discussions of the independence of choice from ZF, as well as providing the framework for pointless topology and Stone spaces.^[33]

An active area of research is the

law of the excluded middle can be formulated in a manner corresponding to the classical formulation in set theory or perhaps in a spectrum of distinct ways unique to type theory. Some of these principles may be proven to be a consequence of other principles. The variety of formulations of these axiomatic principles allows for a detailed analysis of the formulations required in order to derive various mathematical results.^[34][35]

Mathematical education

As set theory gained popularity as a foundation for modern mathematics, there has been support for the idea of introducing the basics of naive set theory early in mathematics education.

In the US in the 1960s, the New Math experiment aimed to teach basic set theory, among other abstract concepts, to primary school students but was met with much criticism.^[36] The math syllabus in European schools followed this trend and currently includes the subject at different levels in all grades. Venn diagrams are widely employed to explain basic set-theoretic relationships to primary school students (even though John Venn originally devised them as part of a procedure to assess the validity of inferences in term logic).

Set theory is used to introduce students to

Boolean logic is used in various programming languages. Likewise, sets and other collection-like objects, such as multisets and lists, are common datatypes in computer science and programming.^[38]

In addition to that, certain sets are commonly used in mathematical teaching, such as the sets ${\displaystyle \mathbb {N} }$ of

natural numbers

, ${\displaystyle \mathbb {Z} }$ of integers, ${\displaystyle \mathbb {R} }$ of

mathematical function as a relation from one set (the domain) to another set (the range).^[39]

See also

• Glossary of set theory
• Class (set theory)
• List of set theory topics
• Relational model – borrows from set theory
• Venn diagram
• Elementary Theory of the Category of Sets
• Structural set theory

Notes

1. ISBN 0-674-32449-8
   (pbk). A synopsis of the history, written by van Heijenoort, can be found in the comments that precede von Neumann's 1925 paper.

1. ^ The objections to Cantor's work were occasionally fierce: Leopold Kronecker's public opposition and personal attacks included describing Cantor as a "scientific charlatan", a "renegade" and a "corrupter of youth". Kronecker objected to Cantor's proofs that the algebraic numbers are countable, and that the transcendental numbers are uncountable, results now included in a standard mathematics curriculum. Writing decades after Cantor's death, Wittgenstein lamented that mathematics is "ridden through and through with the pernicious idioms of set theory", which he dismissed as "utter nonsense" that is "laughable" and "wrong".
2. ^ This is the converse for ZFC; V is a model of ZFC.

Citations

1. ^ Ferreirós, José (2024), "The Early Development of Set Theory", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Winter 2024 ed.), Metaphysics Research Lab, Stanford University, archived from the original on 2023-03-20, retrieved 2025-01-04
2. ISBN 3-7728-0466-7
3. ^ Zenkin, Alexander (2004), "Logic Of Actual Infinity And G. Cantor's Diagonal Proof Of The Uncountability Of The Continuum", The Review of Modern Logic, vol. 9, no. 30, pp. 27–80, archived from the original on 2020-09-22, retrieved 2025-01-04
4. ISBN 9780140147391
5. S2CID 199545885, archived
   from the original on 2012-06-04, retrieved 2013-01-31
6. ISBN 0-87150-154-6
7. ISBN 0-674-34871-0
   .
8. ^ "Introduction to Sets", www.mathsisfun.com, archived from the original on 2006-07-16, retrieved 2020-08-20
9. OCLC 1527264
10. ^ "set theory | Basics, Examples, & Formulas", Encyclopedia Britannica, archived from the original on 2020-08-20, retrieved 2020-08-20
11. ^ Kaplansky, Irving (1972), De Prima, Charles (ed.), Set Theory and Metric Spaces, Boston: Allyn and Bacon, p. 4
12. ^ Kaplansky, Irving (1972), De Prima, Charles (ed.), Set Theory and Metric Spaces, Boston: Allyn and Bacon, p. 5–6
13. ^ Kaplansky, Irving (1972), De Prima, Charles (ed.), Set Theory and Metric Spaces, Boston: Allyn and Bacon, p. 5–6
14. ^ Kaplansky, Irving (1972), De Prima, Charles (ed.), Set Theory and Metric Spaces, Boston: Allyn and Bacon, p. 19
15. ^ Bagaria, Joan (2020), "Set Theory", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Spring 2020 ed.), Metaphysics Research Lab, Stanford University, retrieved 2020-08-20
16. S2CID 15231169
17. doi:10.1090/S0002-9904-1977-14398-X
18. ^ "6.3: Equivalence Relations and Partitions", Mathematics LibreTexts, 2019-11-25, archived from the original on 2022-08-16, retrieved 2022-07-27
19. ^ "Order Relations and Functions" (PDF), Web.stanford.edu, archived (PDF) from the original on 2022-07-27, retrieved 2022-07-29
20. Zbl 0268.26001
21. ^ "A PARTITION CALCULUS IN SET THEORY" (PDF), Ams.org, retrieved 2022-07-29
22. Zbl 1007.03002
23. ISBN 4-87187-714-0
24. ISBN 0-195-08030-0
25. ^ Rodych, Victor (Jan 31, 2018), "Wittgenstein's Philosophy of Mathematics", in Zalta, Edward N. (ed.), Stanford Encyclopedia of Philosophy (Spring 2018 ed.)
26. ISBN 0-631-19130-5{{citation}}: CS1 maint: publisher location (link
    )
27. ^ Rodych 2018, §2.1: "When we prove a theorem or decide a proposition, we operate in a purely formal, syntactical manner. In doing mathematics, we do not discover pre-existing truths that were 'already there without one knowing' (PG 481)—we invent mathematics, bit-by-little-bit." Note, however, that Wittgenstein does not identify such deduction with philosophical logic; cf. Rodych §1, paras. 7-12.
28. ^ Rodych 2018, §3.4: "Given that mathematics is a 'motley of techniques of proof' (RFM III, §46), it does not require a foundation (RFM VII, §16) and it cannot be given a self-evident foundation (PR §160; WVC 34 & 62; RFM IV, §3). Since set theory was invented to provide mathematics with a foundation, it is, minimally, unnecessary."
29. ^ Rodych 2018, §2.2: "An expression quantifying over an infinite domain is never a meaningful proposition, not even when we have proved, for instance, that a particular number n has a particular property."
30. ^ Rodych 2018, §3.6.
31. doi:10.1002/cpa.3160330503
32. ISBN 0-198-53807-3
33. ISBN 978-0-387-97710-2
34. ^ homotopy type theory at the nLab
35. ^ Homotopy Type Theory: Univalent Foundations of Mathematics Archived 2021-01-22 at the Wayback Machine. The Univalent Foundations Program. Institute for Advanced Study.
36. ^ Taylor, Melissa August, Harriet Barovick, Michelle Derrow, Tam Gray, Daniel S. Levy, Lina Lofaro, David Spitz, Joel Stein and Chris (14 June 1999), "The 100 Worst Ideas Of The Century", TIME, archived from the original on 12 April 2025, retrieved 12 April 2025{{cite magazine}}: CS1 maint: multiple names: authors list (link)
37. ISBN 978-1-4411-7413-0
38. ISSN 1469-7653
    , retrieved 12 April 2025
39. ISBN 978-1-4939-2711-1

References

• ISBN 0-444-85401-0
• Johnson, Philip (1972), A History of Set Theory, Prindle, Weber & Schmidt,
  ISBN 0-87150-154-6

• ISBN 0-387-94094-4
• Ferreirós, Jose (2001), Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics, Berlin: Springer,
  ISBN 978-3-7643-5749-8
• Monk, J. Donald (1969), Introduction to Set Theory, McGraw-Hill Book Company,
  ISBN 978-0-898-74006-6
• Potter, Michael (2004), Set Theory and Its Philosophy: A Critical Introduction,
  ISBN 978-0-191-55643-2
• ISBN 978-0-486-47484-7
• ISBN 978-0-486-43520-6
• JSTOR 2708842
• Dauben, Joseph W. (1979), [Unavailable on archive.org] Georg Cantor: his mathematics and philosophy of the infinite, Boston: Harvard University Press,
  ISBN 978-0-691-02447-9

External links

Wikibooks has a book on the topic of: Discrete mathematics/Set theory

• Daniel Cunningham, Set Theory article in the Internet Encyclopedia of Philosophy.
• Jose Ferreiros, "The Early Development of Set Theory" article in the [Stanford Encyclopedia of Philosophy].
• Foreman, Matthew, Akihiro Kanamori, eds. Handbook of Set Theory. 3 vols., 2010. Each chapter surveys some aspect of contemporary research in set theory. Does not cover established elementary set theory, on which see Devlin (1993).
• "Axiomatic set theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Set theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Klein's encyclopedia
  .
• Online books, and library resources in your library and in other libraries about set theory
• University of Wisconsin-Milwaukee, archived from the original on 2021-10-31 – via YouTube