Кристаллическая решётка

В статье есть список источников, но не хватает сносок. Без сносок сложно определить, из какого источника взято каждое отдельное утверждение. Вы можете улучшить статью, проставив сноски на источники, подтверждающие информацию. Сведения без сносок могут быть удалены. (12 августа 2020)

Кристалли́ческая решётка — вспомогательный геометрический образ, вводимый для анализа строения

В зависимости от пространственной симметрии, все кристаллические решётки подразделяются на семь

Помимо основных трансляций, на которых строится элементарная ячейка, в кристаллической решётке могут присутствовать дополнительные трансляции, называемые решётками Браве. В трёхмерных решётках бывают гранецентрированная (F), объёмноцентрированная (I), базоцентрированная (A, B или C), примитивная (P) и ромбоэдрическая (R) решётки Браве. Примитивная система трансляций состоит из множества векторов (a, b, c), во все остальные входят одна или несколько дополнительных трансляций. Так, в объёмноцентрированную систему трансляций Браве входит четыре вектора (a, b, c, ½(a+b+c)), в гранецентрированную — шесть (a, b, c, ½(a+b), ½(b+c), ½(a+c)). Базоцентрированные системы трансляций содержат по четыре вектора: A включает вектора (a, b, c, ½(b+c)), B — вектора (a, b, c, ½(a+c)), а C — (a, b, c, ½(a+b)), центрируя одну из граней элементарного объёма. В системе трансляций Браве R дополнительные трансляции возникают только при выборе гексагональной элементарной ячейки и в этом случае в систему трансляций R входят вектора (a, b, c, ¹/₃(a+b+c), —¹/₃(a+b+c)).

Типы центрировок решёток Браве
Примитивная	Базоцентрированная	Гранецентрированная	Объёмноцентрированная	Дважды-объёмноцентрированная (Ромбоэдрическая)

Сингонии:

• Низшая категория (все трансляции не равны друг другу)
  • Триклинная: ${\displaystyle a\neq b\neq c}$, ${\displaystyle \alpha \neq \beta \neq \gamma \neq 90^{\circ }}$
  • Моноклинная: ${\displaystyle a\neq b\neq c}$, ${\displaystyle \alpha =\gamma =90^{\circ },\beta \neq 90^{\circ }}$
  • Ромбическая: ${\displaystyle a\neq b\neq c}$, ${\displaystyle \alpha =\beta =\gamma =90^{\circ }}$

• Средняя категория (две трансляции из трёх равны между собой)
  • Тетрагональная: ${\displaystyle a=b\neq c}$, ${\displaystyle \alpha =\beta =\gamma =90^{\circ }}$
  • Гексагональная: ${\displaystyle a=b\neq c}$, ${\displaystyle \alpha =\beta =90^{\circ },\gamma =120^{\circ }}$
  • Тригональная: ${\displaystyle a=b=c}$, ${\displaystyle \alpha =\beta =\gamma <120^{\circ }\neq 90^{\circ }}$

• Высшая категория (все трансляции равны между собой)
  • Кубическая: ${\displaystyle a=b=c}$, ${\displaystyle \alpha =\beta =\gamma =90^{\circ }}$

Сингония	Тип центрировки ячейки Браве
	примитивная	базо- центрированная	объёмно- центрированная	гране- центрированная	дважды объёмно- центрированная
Триклинная (параллелепипед)
Моноклинная (призма с параллелограммом в основании)
Ромбическая (прямоугольный параллелепипед)
Тетрагональная (прямоугольный параллелепипед с квадратом в основании)
Гексагональная (призма с основанием правильного центрированного шестиугольника)
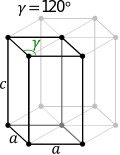Тригональная (равносторонний параллелепипед —ромбоэдр)
Кубическая (куб)

Объём элементарной ячейки в общем случае вычисляется по формуле:

${\displaystyle {\mathsf {V=abc{\sqrt {1-\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma +2\cos \alpha \cos \beta \cos \gamma }}}}}$

• Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 3-е, доп. — М.: Наука, 1976. — 584 с. — («Теоретическая физика», том V). — Глава XIII
• Н. Ашкрофт, Н. Мермин Физика твёрдого тела. Том I.
• Ф. Ф. Греков, Г. Б. Рябенко, Ю. П. Смирнов Структурная кристаллография — Л.:издательство ЛГПИ, 1988.

• Геометрия как искусство.