Самофокусировка

Самофокусировка света — один из эффектов самовоздействия света, состоящий в концентрации энергии

.

В 1988 году за открытие и исследование эффекта самофокусировки Ленинской премией были награждены Г. А. Аскарьян, В. Н. Луговой, В. В. Коробкин, А. П. Сухоруков, Н. В. Пилипецкий и В. И. Таланов.

Эффекты самовоздействия света обусловлены зависимостью свойств среды (

(ориентационным и электронным), тепловыми эффектами и т. д.

Особый интерес представляет рассмотрение ограниченных пучков. В этом случае возникает так называемая нелинейная рефракция: в поле ограниченного пучка

в поле пучка (то есть от знака нелинейности), наблюдается концентрация энергии или, наоборот, её рассеяние.

Рассмотрим световой пучок радиуса ${\displaystyle a}$, распространяющийся в среде с кубичной (керровской) нелинейностью (рис. 1):

${\displaystyle n=n_{0}+n_{2}|A|^{2}}$, или ${\displaystyle \epsilon =\epsilon _{0}+\epsilon _{2}|A|^{2}}$,

где ${\displaystyle \epsilon _{0}={n_{0}}^{2}}$ — линейная часть диэлектрической проницаемости, ${\displaystyle \epsilon _{2}=2n_{2}\epsilon _{0}/n_{0}}$ — коэффициент нелинейности, ${\displaystyle A}$ — амплитуда световой волны. В общем случае коэффициент нелинейности является комплексным ${\displaystyle \epsilon _{2}=\epsilon '_{2}+i\epsilon ''_{2}}$, то есть имеет место нелинейное поглощение.

Пусть ${\displaystyle \epsilon ''_{2}=0}$. Самофокусировка наблюдается в том случае, если ${\displaystyle \epsilon '_{2}>0}$, так что внутри пучка

лучей. Его критический угол равен ${\displaystyle \theta _{0}=\arccos \left({\frac {n_{0}}{n_{0}+n_{2}|A|^{2}}}\right)}$. Лучи, идущие под углом ${\displaystyle \theta >\theta _{0}}$, покидают пучок, а те, для которых ${\displaystyle \theta <\theta _{0}}$, отклонятся к оси пучка. Расхождение лучей в пучке с плоским фазовым фронтом определяется углом ${\displaystyle \theta _{d}={\frac {0.61\lambda _{0}}{n_{0}a}}}$, где ${\displaystyle \lambda _{0}}$ — длина волны света в вакууме. В зависимости от соотношения углов ${\displaystyle \theta _{0}}$ и ${\displaystyle \theta _{d}}$ возможны следующие физические ситуации:

• если ${\displaystyle \theta _{0}<\theta _{d}}$, пучок расплывается, однако медленнее, чем в линейной среде;
• если ${\displaystyle \theta _{0}=\theta _{d}}$, дифракционное расплывание полностью компенсируется нелинейной рефракцией. Формируется своеобразный диэлектрический волновод, по которому пучок распространяется без расходимости. Этот режим называется самоканализацией пучка. Критическая мощность излучения, при которой возникает этот эффект, может быть оценена как ${\displaystyle P_{c}={\frac {(1.22)^{2}\lambda _{0}^{2}c}{256n_{2}}}}$. Явление самоканализации во многом аналогично так называемому солитонному режиму распространения света, при котором дисперсионное расплывание волнового пакета (импульса, то есть ограниченного во времени пучка) точно уравновешивается нелинейным сжатием за счёт фазовой самомодуляции. Для наиболее распространённых в практических приложениях гауссовых пучков говорят о квазисолитонном режиме и солитоноподобных пучках в нелинейной среде. Следует отметить, что, в отличие от случая самоканализации, солитон представляет собой устойчивое образование.
• если ${\displaystyle \theta _{0}>\theta _{d}}$ (или ${\displaystyle P>P_{c}}$), лучи отклоняются к оси пучка — происходит самофокусировка. Нелинейная среда действует подобно
  собирающей линзе, фокусное расстояние
  которой можно оценить, если ввести так называемую дифракционную длину ${\displaystyle R_{d}={\frac {k_{0}a^{2}}{2}}\approx {\frac {a}{\theta _{d}}}}$ (${\displaystyle k_{0}=2\pi /\lambda _{0}}$ — волновое число). Тогда условие ${\displaystyle \theta _{0}=\theta _{d}}$ эквивалентно ${\displaystyle R_{d}={\frac {a}{2}}{\sqrt {\frac {n_{0}}{n_{2}|A|^{2}}}}=R_{nl}}$, где ${\displaystyle R_{nl}}$ называется нелинейной длиной, или длиной самофокусировки. В случае большой мощности (${\displaystyle P>>P_{c}}$) поведение пучка может быть описано в приближении геометрической оптики, а фокусное расстояние составляет ${\displaystyle z_{f}\approx R_{nl}}$.

В случае ${\displaystyle \epsilon '_{2}<0}$ (уменьшение показателя преломления в поле пучка) имеет место самодефокусировка света.

Для воздуха (газов) критическая мощность обычно составляет единицы

.

Описание возникновения фокусов может быть дано на основании

в приближении медленного (по сравнению с периодом колебаний и длиной волны света) изменения амплитуды волны:

${\displaystyle \Delta _{\bot }E+2ik\left({\frac {\partial E}{\partial z}}+{\frac {1}{v}}{\frac {\partial E}{\partial t}}\right)+k^{2}{\frac {\delta \epsilon }{\epsilon _{0}}}E=0}$,

где ${\displaystyle E}$ —

напряженность электрического поля

волны, ${\displaystyle v=c/n_{0}}$, ${\displaystyle \delta \epsilon =\epsilon _{2}|E|^{2}}$, ${\displaystyle \Delta _{\bot }={\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}}$ — поперечный

нелинейного уравнения Шредингера

:

${\displaystyle \Delta _{\bot }E+2ik{\frac {\partial E}{\partial z}}+k^{2}{\frac {\delta \epsilon }{\epsilon _{0}}}E=0}$.

Приближенные аналитические решения этого уравнения не содержат ряда существенных особенностей, которые могут быть выявлены лишь при численном анализе. Так, аппроксимация численных результатов дает для положения фокуса оценку ${\displaystyle z_{f}\approx \xi {\frac {ka^{2}}{{\sqrt {P/P_{c}}}-1}}}$, где ${\displaystyle \xi }$ — некоторая константа. При этом возрастание интенсивности в области фокуса ограничивается эффектами нелинейного поглощения, связанными с комплексной частью коэффициента нелинейности ${\displaystyle \epsilon ''_{2}}$ (

и т. д.)

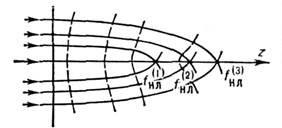
Результаты численных расчетов позволяют также выявить многофокусную структуру процесса самофокусировки. На оси пучка формируется ряд

, отвечающих последовательной фокусировке различных кольцевых зон пучка (см. рис. 2). В каждый фокус втекает (и частично поглощается) мощность порядка критической. Полное число фокусов ограничено первоначальной мощностью пучка, а также величиной поглощения.

При учете нестационарности (короткие импульсы) в системе наблюдаются движущиеся фокусы, а также их раздвоение: один фокус движется в направлении распространения падающего импульса (скорость фокуса может превышать скорость света в среде), а второй сначала движется навстречу пучку, затем останавливается и идет по направлению его распространения. Нестационарность может быть также связана с проявлениями инерционности нелинейности.

Наличие самофокусировки может также приводить к неустойчивости пучка, то есть к экспоненциальному возрастанию малых пространственных

интенсивности. В результате пучок разбивается на отдельные нити радиусом ${\displaystyle a_{opt}={\frac {1}{k_{0}}}{\sqrt {\frac {n_{0}}{n_{2}|A|^{2}}}}}$ и мощностью ${\displaystyle P_{c}}$.

• Фазовая самомодуляция
• Самодефокусировка света
• Самоканализация света
• Солитон
• Нелинейная оптика
• Фемтофизика

Литература

• А. П. Сухоруков. Самофокусировка света. // Физическая энциклопедия. — Т. 4. — М.: БРЭ, 1994. — С. 415—417.
• УФН
  . — 1967. — Т. 93, вып. 9. — С. 19-70.
• УФН
  . — 1973. — Т. 111, вып. 10. — С. 249-260.
• В. Н. Луговой,
  УФН
  . — 1973. — Т. 111, вып. 10. — С. 203-247.
• И. Р. Шен. Принципы нелинейной оптики. — М.: Мир, 1989.
• Н. И. Коротеев, И. Л. Шумай. Физика мощного лазерного излучения. — М.: Наука, 1991.
• Власов С. Н., Таланов В. И. Самофокусировка волн. — Н. Новгород: ИПФ РАН, 1997. — 220 с. Архивная копия от 18 апреля 2014 на Wayback Machine
• С. В. Чекалин, В. П. Кандидов. От самофокусировки световых пучков — к филаментации лазерных импульсов //
  УФН
  . — 2013. — Т. 183. — С. 133—152.

Для улучшения этой статьи по физике желательно: Оформить список литературы. Проставить сноски, внести более точные указания на источники. Пожалуйста, после исправления проблемы исключите её из списка параметров. После устранения всех недостатков этот шаблон может быть удалён любым участником.