RSA
| RSA | |
|---|---|
| Дата возникновения | 1977[1] |
| Названо в честь | Рональд Линн Ривест, Ади Шамир и Леонард Макс Адлеман |
| Определяющая формула | [2] |
| Обозначение в формуле | , , и |
RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших полупростых чисел.
Криптосистема RSA стала первой системой, пригодной и для
История
Алгоритм шифрования с открытым и закрытым ключом приписывается Уитфилду Диффи и Мартину Хеллману, которые опубликовали эту концепцию в 1976 году. Они также ввели цифровые подписи и попытались применить теорию чисел. В их формулировке использовался секретный ключ с общим доступом, созданный путем экспоненциализации некоторого числа, простого по модулю. Однако они оставили открытой проблему реализации односторонней функции, возможно потому, что сложность факторизации в то время не была хорошо изучена.
Рон Ривест, Ади Шамир и Леонард Адлеман из Массачусетского технологического института в течение года предприняли несколько попыток создать одностороннюю функцию, которую было бы трудно инвертировать. Ривест и Шамир, будучи компьютерными учеными, предложили множество потенциальных функций, а Адлеман, будучи математиком, отвечал за поиск их слабых мест. Они опробовали множество подходов, включая "ранцевый" и "перестановочные полиномы". Какое-то время они думали, что то, чего они хотели достичь, невозможно из-за противоречивых требований. В апреле 1977 года они провели Песах в доме одного из студентов и выпили много манишевицкого вина, а затем вернулись к себе домой около полуночи. Ривест, не в силах заснуть, лег на диван с учебником математики и начал думать о своей односторонней функции. Остаток ночи он провел, формализуя свою идею, и к рассвету большая часть статьи была готова. Алгоритм теперь известен как RSA - инициалы их фамилий в том же порядке, что и в их статье.
Клиффорд Кокс, английский математик, работавший в британской разведывательной службе Government Communications Headquarters (GCHQ), описал эквивалентную систему во внутреннем документе в 1973 г. Однако, учитывая относительно дорогие компьютеры, необходимые для ее реализации в то время, она считалась в основном курьезом и, насколько известно, так и не была применена. Однако его открытие было раскрыто только в 1997 году из-за его сверхсильного засекречивания.
В августе 1977 года в колонке «Математические игры» Мартина Гарднера в журнале Scientific American с разрешения Рональда Ривеста[4] появилось первое описание криптосистемы RSA[5]. Читателям также было предложено дешифровать английскую фразу, зашифрованную описанным алгоритмом:
- 9686
- 1477
- 8829
- 7431
- 0816
- 3569
- 8962
- 1829
- 9613
- 1409
- 0575
- 9874
- 2982
- 3147
- 8013
- 9451
- 7546
- 2225
- 9991
- 6951
- 2514
- 6622
- 3919
- 5781
- 2206
- 4355
- 1245
- 2093
- 5708
- 8839
- 9055
- 5154
В качестве открытых параметров системы были использованы числа n=1143816...6879541 (129 десятичных знаков, 425
После публикации Мартина Гарднера полное описание новой криптосистемы любой желающий мог получить, выслав по почте запрос Рональду Ривесту с приложенным конвертом с обратным адресом и марками на 35 центов.[5] Полное описание новой криптосистемы было опубликовано в журнале «Communications of the ACM» в феврале 1978 года[9].
Заявка на патент была подана 14 декабря 1977 года, в качестве владельца был указан MIT. Патент 4405829 был выдан 20 сентября 1983 года, а 21 сентября 2000 года срок его действия истёк[10]. Однако за пределами США у изобретателей патента на алгоритм не было, так как в большинстве стран его необходимо было получить до первой публикации[11].
В 1982 году Ривест, Шамир и Адлеман организовали компанию RSA Data Security[англ.] (в настоящий момент — подразделение EMC). В 1989 году RSA, вместе с симметричным шифром DES, упоминается в RFC 1115, тем самым начиная использование алгоритма в зарождающейся сети Internet[12], а в 1990 году использовать алгоритм начинает министерство обороны США[13].
В ноябре 1993 года открыто публикуется версия 1.5 стандарта PKCS1[англ.], описывающего применение RSA для шифрования и создания электронной подписи. Последние версии стандарта также доступны в виде RFC (RFC 2313 — 1.5, 1993 год; RFC 2437 — 2.0, 1998 год; RFC 3447 — 2.1, 2002 год).
В декабре 1997 года была обнародована информация о приоритете Клиффорда Кокса[14].
Описание алгоритма
Введение
Криптографические системы с открытым ключом используют так называемые односторонние функции, которые обладают следующим свойством:
- если известно , то вычислить относительно просто;
- если известно , то для вычисления нет простого (эффективного) пути.
Под односторонностью понимается не математически доказанная однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.
В основу криптографической системы с открытым ключом RSA положена сложность задачи факторизации произведения двух больших простых чисел. Для шифрования используется операция возведения в степень по модулю большого числа. Для дешифрования (обратной операции) за разумное время необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложение числа на простые множители.
В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (англ. public key), так и закрытым ключом (англ. private key). В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями в криптосистеме RSA образуют «согласованную пару» в том смысле, что они являются взаимно обратными, то есть:
- допустимых пар открытого и закрытого ключей
- соответствующие функции шифрования и расшифрования такие, что
- сообщения , где — множество допустимых сообщений,
- сообщения , где — множество допустимых сообщений,
- соответствующие функции шифрования и расшифрования такие, что
Алгоритм создания открытого и секретного ключей
RSA-ключи генерируются следующим образом[15]:
- 1) выбираются два различных случайных простых числа и заданного размера (например, 1024 бита каждое);
- 2) вычисляется их произведение , которое называется модулем;
- 3) вычисляется значение функции Эйлера от числа :
- ;
- 4) выбирается целое число (), взаимно простое со значением функции ;
- 5) вычисляется число , мультипликативно обратное к числу по модулю , то есть число, удовлетворяющее сравнению:
- (число называется секретной экспонентой; обычно оно вычисляется при помощи расширенного алгоритма Евклида);
- 6) пара публикуется в качестве открытого ключа RSA (англ. RSA public key);
- 7) пара играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете.
Шифрование и расшифрование
Предположим, Боб хочет послать Алисе сообщение .
Сообщениями являются целые числа в интервале от до . [15]

|
Алгоритм шифрования[15]:
|
Алгоритм расшифрования:
|
Данная схема на практике не используется по причине того, что она не является практически надёжной (semantically secured). Действительно, односторонняя функция E(m) является детерминированной — при одних и тех же значениях входных параметров (ключа и сообщения) выдаёт одинаковый результат. Это значит, что не выполняется необходимое условие практической (семантической) надёжности шифра.
Алгоритм шифрования сеансового ключа
Более надёжным является смешанный алгоритм шифрования, в котором сначала шифруется сеансовый ключ, а потом уже с его помощью участники шифруют свои сообщения симметричными системами. После завершения сеанса сеансовый ключ, как правило, уничтожается.
Алгоритм шифрования сеансового ключа выглядит следующим образом[17]:

|
Алгоритм:
|
Алгоритм:
|
В случае, когда сеансовый ключ больше, чем модуль , сеансовый ключ разбивают на блоки нужной длины (в случае необходимости дополняют нулями) и шифруют каждый блок.
Корректность схемы RSA
- Уравнения и , на которых основана схема RSA, определяют взаимно обратные преобразования множества
Действительно, для
Покажем, что:
- .
Возможны два случая:
- .
Поскольку числа и являются взаимно обратными относительно умножения по модулю , т.e
- для некоторого целого ,
тогда:
где второе тождество следует из теоремы Ферма.
- Рассмотрим второй случай:
- ,
тогда
Таким образом, при всех выполняется равенство
Аналогично можно показать, что:
- .
Тогда, из китайской теоремы об остатках
Пример
| Этап | Описание операции | Результат операции |
|---|---|---|
| Генерация ключей | Выбрать два простых различных числа |
|
| Вычислить произведение |
| |
| Вычислить функцию Эйлера |
| |
| Выбрать открытую экспоненту |
| |
| Вычислить секретную экспоненту |
| |
| Опубликовать открытый ключ |
| |
| Сохранить закрытый ключ |
| |
| Шифрование | Выбрать текст для зашифрования |
|
| Вычислить шифротекст |
| |
| Расшифрование | Вычислить исходное сообщение |
|
Цифровая подпись
Система RSA может использоваться не только для шифрования, но и для
Предположим, что Алисе (стороне ) нужно отправить Бобу (стороне ) сообщение , подтверждённое
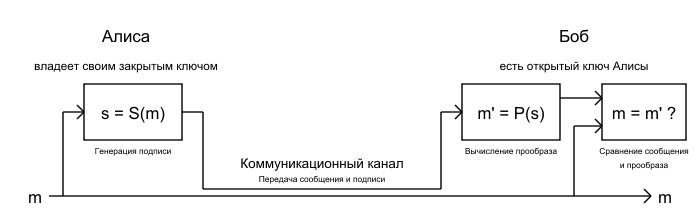
|
Алгоритм:
|
Алгоритм:
|
Поскольку
Важное свойство цифровой подписи заключается в том, что её может проверить каждый, кто имеет доступ к открытому ключу её автора. Один из участников обмена сообщениями после проверки подлинности цифровой подписи может передать подписанное сообщение ещё кому-то, кто тоже в состоянии проверить эту подпись. Например, сторона может переслать стороне электронный чек. После того как сторона проверит подпись стороны на чеке, она может передать его в свой банк, служащие которого также имеют возможность проверить подпись и осуществить соответствующую денежную операцию.
Заметим, что подписанное сообщение не зашифровано. Оно пересылается в исходном виде и его содержимое не защищено от нарушения конфиденциальности. Путём совместного применения представленных выше схем шифрования и цифровой подписи в системе RSA можно создавать сообщения, которые будут и зашифрованы, и содержать цифровую подпись. Для этого автор сначала должен добавить к сообщению свою цифровую подпись, а затем — зашифровать получившуюся в результате пару (состоящую из самого сообщения и подписи к нему) с помощью открытого ключа, принадлежащего получателю. Получатель расшифровывает полученное сообщение с помощью своего секретного ключа[17]. Если проводить аналогию с пересылкой обычных бумажных документов, то этот процесс похож на то, как если бы автор документа поставил под ним свою печать, а затем положил его в бумажный конверт и запечатал, с тем чтобы конверт был распечатан только тем человеком, кому адресовано сообщение.
Скорость работы алгоритма RSA
Поскольку генерация ключей происходит значительно реже операций, реализующих шифрование, расшифрование, а также создание и проверку цифровой подписи, задача вычисления представляет основную вычислительную сложность. Эта задача может быть разрешена с помощью
- представим в двоичной системе счисления:
- , где
- положим и затем для вычислим
- найденное и будет искомым значением
Т. к. каждое вычисление на шаге 2 требует не более трёх умножений по модулю и этот шаг выполняется раз, то сложность алгоритма может быть оценена величиной .
Чтобы проанализировать время выполнения операций с открытым и закрытым ключами, предположим, что открытый ключ и закрытый ключ удовлетворяют соотношениям , . Тогда в процессах их применения выполняется соответственно и умножений по модулю.
Таким образом время выполнения операций растёт с увеличением количества ненулевых битов в
По эвристическим оценкам длина секретной экспоненты , нетривиальным образом зависящей от открытой экспоненты и модуля , с большой вероятностью близка к длине . Поэтому расшифрование данных идёт медленнее, чем шифрование, а проверка подписи – быстрее, чем её создание.
Алгоритм RSA намного медленнее, чем
Использование китайской теоремы об остатках для ускорения расшифрования
При расшифровании или подписывании сообщения в алгоритме RSA показатель вычисляемой степени будет довольно большим числом (порядка 1000 бит). Поэтому требуется алгоритм, сокращающий количество операций. Так как числа и в разложении известны владельцу закрытого ключа, то можно вычислить:
Поскольку и — числа порядка на эти действия потребуется два возведения числа в 512-битовую степень по модулю 512-битового числа. Это существенно (для 1024 бит тестирование показало в 3 раза) быстрее, чем одно возведение в 1024-битовую степень по модулю 1024-битового числа. Далее осталось восстановить по и что можно сделать с помощью китайской теоремы об остатках[20].
Криптоанализ RSA
Стойкость алгоритма основывается на сложности вычисления обратной функции к функции шифрования[21]
- .
Для вычисления по известным нужно найти такой , чтобы
то есть найти обратный элемент к в мультипликативной группе вычетов по модулю
Вычисление обратного элемента по модулю не является сложной задачей, однако злоумышленнику неизвестно значение . Для вычисления функции Эйлера от известного числа необходимо знать разложение этого числа на простые множители. Нахождение таких множителей и является сложной задачей, а знание этих множителей — «потайной дверцей» (
- для некоторого .
В 2010 году группе учёных из Швейцарии, Японии, Франции, Нидерландов, Германии и США удалось успешно вычислить данные, зашифрованные при помощи криптографического ключа стандарта RSA длиной 768 бит. Нахождение простых сомножителей осуществлялось общим методом решета числового поля[22]. По словам исследователей, после их работы в качестве надежной системы шифрования можно рассматривать только RSA-ключи длиной 1024 бита и более. Причём от шифрования ключом длиной в 1024 бит стоит отказаться в ближайшие три-четыре года[23]. С 31 декабря 2013 года браузеры Mozilla перестали поддерживать сертификаты удостоверяющих центров с ключами RSA меньше 2048 бит[24].
Кроме того, при неправильной или неоптимальной реализации или использовании алгоритма возможны специальные криптографические атаки, такие как атаки на схемы с малой секретной экспонентой или на схемы с общим выбранным значением модуля.
Атаки на алгоритм RSA
Атака Винера на RSA
В некоторых приложениях требуется ускорить процесс расшифровывания в алгоритме RSA. Поэтому выбирается небольшая расшифровывающая экспонента. В случае когда расшифровывающая экспонента можно определить за полиномиальное время с помощью атаки Винера[20], опирающейся на непрерывные дроби.
при
Целые числа называются непрерывной дробью, представляющей а рациональные числа подходящими дробями. Каждая из подходящих дробей несократима, а скорость роста их знаменателей сравнима с показательной.
Один из важных результатов теории непрерывных дробей:
то одна из подходящих дробей в разложении в непрерывную дробь.
Пусть у нас есть модуль причём Допустим нападающему известна шифрующая экспонента E, обладающая свойством
Так как очевидно Кроме того, так как предполагалось, что Значит,
Поскольку НОД то подходящая дробь в разложении дроби в непрерывную. Таким образом, можно узнать расшифровывающую экспоненту, поочерёдно подставляя знаменатели подходящих дробей в выражение:
для некоторого случайного числа Получив равенство, найдём Общее число подходящих дробей, которое придётся проверить оценивается как
Обобщённая атака Винера
Атака Винера, описанная выше, возможна лишь в том случае, когда атакующему известно о неравенстве
где — секретная экспонента, а — модуль RSA. Боне и Дерфи, используя двумерный аналог Теоремы Копперсмита, смогли обобщить атаку Винера[20] на случай, когда
Атака посредника, или атака «человек посередине»
Атака посредника не опасна если злоумышленник может только прослушивать канал связи по которому передаётся открытый ключ. В этом случае злоумышленник сможет перехватить открытый ключ и зашифрованные сообщения, и подписи. Но при условии, что злоумышленник перехватил ключ и может отправлять сообщения по каналу связи. Злоумышленник может отправлять ложные сообщения.
Применение RSA
Система RSA используется для защиты
Также она используется в открытой системе шифрования
Из-за низкой скорости шифрования сообщения обычно шифруют с помощью более производительных симметричных алгоритмов со случайным сеансовым ключом (например,
Примечания
- ↑ Still Guarding Secrets after Years of Attacks, RSA Earns Accolades for its Founders — Общество промышленной и прикладной математики.
- ↑ Introduction to Modern Cryptography (англ.) — 2 — CRC Press, 2015. — P. 411. — 583 p. — ISBN 978-1-4665-7026-9
- ↑ 1 2 Bakhtiari, Maarof, 2012, p. 175.
- ↑ A Quarter Century of Recreational Mathematics, by Martin Gardner (англ.). Scientific American. — «Ronald L. Rivest of the Massachusetts Institute of Technology allowed me to be the first to reveal—in the August 1977 column—the «publickey» cipher system that he co-invented». Дата обращения: 3 марта 2012. Архивировано из оригинала 23 июня 2012 года.
- ↑ 1 2 Gardner, 1977.
- ↑ Bruce Schneier. Factoring — State of the Art and Predictions (англ.) (12 февраля 1995). Дата обращения: 3 марта 2012. Архивировано из оригинала 23 июня 2012 года.
- ↑ Donald T. Davis. A Discussion of RSA-129 Activity (англ.) (25 ноября 2003). Дата обращения: 3 марта 2012. Архивировано из оригинала 23 июня 2012 года.
- ↑ Чмора А. Л. 4.6.4. Силовая атака на основе распределенных вычислений // Современная прикладная криптография. — 2002. — 2000 экз. — ISBN 5-85438-046-3.
- ↑ Rivest, Shamir, Adleman, 1978.
- ↑ Ronald L. Rivest et al. Cryptographic Communications System and Method
- ↑ Adam Back. PGP Timeline (англ.). Дата обращения: 3 марта 2012. Архивировано из оригинала 23 июня 2012 года.
- ↑ J. Linn. Privacy Enhancement for Internet Electronic Mail: Part III — Algorithms, Modes, and Identifiers (англ.) (август 1989). Дата обращения: 18 марта 2012. Архивировано из оригинала 23 июня 2012 года.
- ↑ RSA Security Inc. Company history (англ.). FundingUniverse. Дата обращения: 18 марта 2012. Архивировано из оригинала 23 июня 2012 года.
- ↑ C. C. Cocks A note on «non-secret encryption» Архивировано 4 августа 2009 года. (англ.) 20 ноября 1973
- ↑ 1 2 3 4 Menezes, Oorschot, Vanstone, 1996, 8.2. RSA public-key encryption.
- ↑ Boneh, 1999.
- ↑ 1 2 Брюс Шнайер. Прикладная криптография 2-е издание протоколы, алгоритмы и исходные тексты на языке C++
- ↑ Rivest, Shamir, Adleman, 1978, pp. 7—8.
- ↑ Rivest, Shamir, Adleman, 1978, p. 8.
- ↑ 1 2 3 Н. СМАРТ Мир программирования Криптография — изд. Техносфера, Москва 2006
- ↑ Ян С. Й. Криптоанализ RSA. — М.—Ижевск: НИЦ «Регулярная и хаотическая динамика», Ижевский институт компьютерных исследований, 2011. — 312 с.
- ↑ Анонс факторизации RSA-768 Архивная копия от 13 апреля 2014 на Wayback Machine (англ.)
- ↑ Факторизация RSA-768 Архивная копия от 13 декабря 2012 на Wayback Machine (англ.)
- ↑ Dates for Phasing out MD5-based signatures and 1024-bit moduli. Дата обращения: 2 марта 2013. Архивировано 20 ноября 2012 года.
Литература
- Diffie W., Hellman M. E. New Directions in Cryptography (англ.) // IEEE Transactions on Information Theory / F. Kschischang — IEEE, 1976. — Vol. 22, Iss. 6. — P. 644—654. — ISSN 0018-9448; 1557-9654 — doi:10.1109/TIT.1976.1055638
- Gardner M. A New Kind of Cipher that Would Take Millions of Years to Break (англ.) // Scientific American — New York City: NPG, 1977. — Vol. 237, Iss. 2. — P. 120—124. — 5 p. — ISSN 0036-8733; 1946-7087 — doi:10.1038/SCIENTIFICAMERICAN0877-120
- Rivest R., Shamir A., Adleman L. A method for obtaining digital signatures and public-key cryptosystems (англ.) // Communications of the ACM — New York City: Association for Computing Machinery, 1978. — Vol. 21, Iss. 2. — P. 120—126. — ISSN 0001-0782; 1557-7317 — doi:10.1145/359340.359342
- Menezes A. J., Oorschot P. v., Vanstone S. A. Handbook of Applied Cryptography (англ.) — Boca Raton: CRC Press, 1996. — 816 p. — (Discrete Mathematics and Its Applications) — ISBN 978-0-8493-8523-0
- Boneh D. Twenty Years of attacks on the RSA Cryptosystem (англ.) // Notices of the American Mathematical Society / F. Morgan — AMS, 1999. — Vol. 46, Iss. 2. — P. 203–213. — ISSN 0002-9920; 1088-9477
- Bakhtiari M., Maarof M. A. Serious Security Weakness in RSA Cryptosystem (англ.) // International Journal of Computer Science Issues — 2012. — Vol. 9, Iss. 1, No 3. — P. 175—178. — ISSN 1694-0814; 1694-0784
- Нильс Фергюсон, Брюс Шнайер. Практическая криптография = Practical Cryptography: Designing and Implementing Secure Cryptographic Systems. — М. : Диалектика, 2004. — 432 с. — 3000 экз. — ISBN 5-8459-0733-0, ISBN 0-4712-2357-3.
- Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.







































































































































