Regular map (graph theory)

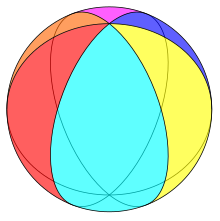
In

.

Overview

Regular maps are typically defined and studied in three ways: topologically, group-theoretically, and graph-theoretically.

Topological approach

Topologically, a map is a 2-cell decomposition of a compact connected 2-manifold.^[1]

The genus g, of a map M is given by Euler's relation ${\displaystyle \chi (M)=|V|-|E|+|F|}$ which is equal to ${\displaystyle 2-2g}$ if the map is orientable, and ${\displaystyle 2-g}$ if the map is non-orientable. It is a crucial fact that there is a finite (non-zero) number of regular maps for every orientable genus except the torus.

Group-theoretical approach

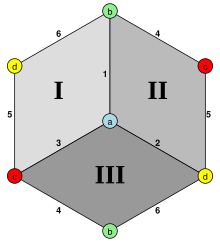
Group-theoretically, the permutation representation of a regular map M is a transitive permutation group C, on a set ${\displaystyle \Omega }$ of flags, generated by three fixed-point free involutions r₀, r₁, r₂ satisfying (r₀r₂)²= I. In this definition the faces are the orbits of F = <r₀, r₁>, edges are the orbits of E = <r₀, r₂>, and vertices are the orbits of V = <r₁, r₂>. More abstractly, the automorphism group of any regular map is the non-degenerate, homomorphic image of a <2,m,n>-triangle group.

Graph-theoretical approach

Graph-theoretically, a map is a cubic graph ${\displaystyle \Gamma }$ with edges coloured blue, yellow, red such that: ${\displaystyle \Gamma }$ is connected, every vertex is incident to one edge of each colour, and cycles of edges not coloured yellow have length 4. Note that ${\displaystyle \Gamma }$ is the flag graph or graph-encoded map (GEM) of the map, defined on the vertex set of flags ${\displaystyle \Omega }$ and is not the skeleton G = (V,E) of the map. In general, |${\displaystyle \Omega }$| = 4|E|.

A map M is regular if Aut(M)

on the flags. Aut(M) of a regular map is transitive on the vertices, edges, and faces of M. A map M is said to be reflexible iff Aut(M) is regular and contains an automorphism ${\displaystyle \phi }$ that fixes both a vertex v and a face f, but reverses the order of the edges. A map which is regular but not reflexible is said to be chiral.

Examples

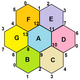
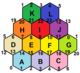
• The great dodecahedron is a regular map with pentagonal faces in the orientable surface of genus 4.
• The hemicube is a regular map of type {4,3} in the projective plane.
• The hemi-dodecahedron is a regular map produced by pentagonal embedding of the Petersen graph in the projective plane.
• The p-hosohedron is a regular map of type {2,p}.
• The
  Dyck map is a regular map of 12 octagons on a genus-3 surface. Its underlying graph, the Dyck graph
  , can also form a regular map of 16 hexagons in a torus.

The following is a complete list of regular maps in surfaces of positive Euler characteristic, χ: the sphere and the projective plane.^[2]

χ	g	Schläfli	Vert.	Edges	Faces	Group	Order	Graph		Notes
2	0	{p,2}	p	p	2	C2 × Dihp	4p	Cp		Dihedron
2	0	{2,p}	2	p	p	C2 × Dihp	4p	p-fold K2		Hosohedron
2	0	{3,3}	4	6	4	S4	24	K4		Tetrahedron
2	0	{4,3}	8	12	6	C2 × S4	48	K4 × K2		Cube
2	0	{3,4}	6	12	8	C2 × S4	48	K2,2,2		Octahedron
2	0	{5,3}	20	30	12	C2 × A5	120			Dodecahedron
2	0	{3,5}	12	30	20	C2 × A5	120	K6 × K2		Icosahedron
1	n1	{2p,2}/2	p	p	1	Dih2p	4p	Cp		Hemi-dihedron[3]
1	n1	{2,2p}/2	2	p	p	Dih2p	4p	p-fold K2		Hemi-hosohedron[3]
1	n1	{4,3}/2	4	6	3	S4	24	K4		Hemicube
1	n1	{3,4}/2	3	6	4	S4	24	2-fold K3		Hemioctahedron
1	n1	{5,3}/2	10	15	6	A5	60	Petersen graph		Hemidodecahedron
1	n1	{3,5}/2	6	15	10	A5	60	K6		Hemi-icosahedron

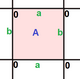
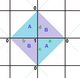
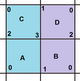
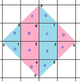
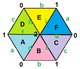
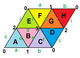
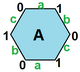
The images below show three of the 20 regular maps in the

, labelled with their Schläfli types.

• 
  {6,4}
• 
  {4,8}
• 
  {8,4}

Toroidal polyhedra

Example visualized as nets

{4,4}1,0 (v:1, e:2, f:1)	{4,4}1,1 (v:2, e:4, f:2)	{4,4}2,0 (v:4, e:8, f:4)	{4,4}2,1 (v:5, e:10, f:5)	{4,4}2,2 (v:8, e:16, f:8)
{3,6}1,0 (v:1, e:3, f:2)	{3,6}1,1 (v:3, e:9, f:6)	{3,6}2,0 (v:4, e:12, f:8)	{3,6}2,1 (v:7, e:21, f:14)	{3,6}2,2 (v:12, e:36, f:24)
{6,3}1,0 (v:2, e:3, f:1)	{6,3}1,1 (v:6, e:9, f:3)	{6,3}2,0 (v:8, e:12, f:4)	{6,3}2,1 (v:14, e:21, f:7)	{6,3}2,2 (v:24, e:36, f:12)

Regular maps exist as torohedral polyhedra as finite portions of Euclidean tilings, wrapped onto the surface of a

There are 2 special cases (b,0) and (b,b) with reflective symmetry, while the general cases exist in chiral pairs (b,c) and (c,b).

Regular maps of the form {4,4}_m,0 can be represented as the finite regular skew polyhedron {4,4 | m}, seen as the square faces of a m×m duoprism in 4-dimensions.

Here's an example {4,4}_8,0 mapped from a plane as a chessboard to a cylinder section to a torus. The projection from a cylinder to a torus distorts the geometry in 3 dimensions, but can be done without distortion in 4-dimensions.

Regular maps with zero Euler characteristic^[6]

χ	g	Schläfli	Vert.	Edges	Faces	Group	Order	Notes
0	1	{4,4}b,0 n=b2	n	2n	n	[4,4](b,0)	8n	Flat toroidal polyhedra Same as {4,4 | b}
0	1	{4,4}b,b n=2b2	n	2n	n	[4,4](b,b)	8n	Flat toroidal polyhedra Same as rectified {4,4 | b}
0	1	{4,4}b,c n=b2+c2	n	2n	n	[4,4]+ (b,c)	4n	Flat chiral toroidal polyhedra
0	1	{3,6}b,0 t=b2	t	3t	2t	[3,6](b,0)	12t	Flat toroidal polyhedra
0	1	{3,6}b,b t=3b2	t	3t	2t	[3,6](b,b)	12t	Flat toroidal polyhedra
0	1	{3,6}b,c t=b2+bc+c2	t	3t	2t	[3,6]+ (b,c)	6t	Flat chiral toroidal polyhedra
0	1	{6,3}b,0 t=b2	2t	3t	t	[3,6](b,0)	12t	Flat toroidal polyhedra
0	1	{6,3}b,b t=3b2	2t	3t	t	[3,6](b,b)	12t	Flat toroidal polyhedra
0	1	{6,3}b,c t=b2+bc+c2	2t	3t	t	[3,6]+ (b,c)	6t	Flat chiral toroidal polyhedra

In generally regular toroidal polyhedra {p,q}_b,c can be defined if either p or q are even, although only euclidean ones above can exist as toroidal polyhedra in 4-dimensions. In {2p,q}, the paths (b,c) can be defined as stepping face-edge-face in straight lines, while the dual {p,2q} forms will see the paths (b,c) as stepping vertex-edge-vertex in straight lines.

Hyperbolic regular maps

The map {6,4}3 can be seen as {6,4}4,0. Following opposite edges will traverse all 4 hexagons in sequence. It exists in the petrial octahedron , {3,4}π with 6 vertices, 12 edges and 4 skew hexagon faces.

Branko Grunbaum identified a double-covered cube {8/2,3}, with 6 octagonal faces, double wrapped, needing 24 edges, and 16 vertices. It can be seen as regular map {8,3}_2,0 on a hyperbolic plane with 6 colored octagons.^[7]

See also

• Topological graph theory
• Abstract polytope
• Planar graph
• Toroidal graph
• Graph embedding
• Regular tiling
• Platonic solid
• Platonic graph

References

Bibliography

• ISBN 978-0-387-09212-6
  .
• doi:10.1145/1531326.1531355, archived from the original
  (PDF) on 2011-06-09.
• doi:10.1006/jctb.2000.2008
  .
• Nedela, Roman (2007), Maps, Hypermaps, and Related Topics (PDF).
• Vince, Andrew (2004), "Maps", Handbook of Graph Theory.
• Brehm, Ulrich; Schulte, Egon (2004), "Polyhedral Maps", Handbook of Discrete and Computational Geometry.
• Séquin, Carlo (2013), "Symmetrical immersions of low-genus non-orientable regular maps" (PDF), Berkeley University.