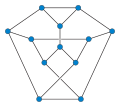
Tietze's graph

Source: Wikipedia, the free encyclopedia.
Tietze's subdivision of a Möbius strip into six mutually-adjacent regions. The vertices and edges of the subdivision form an embedding of Tietze's graph onto the strip.
Tietze's graph
Chromatic index
4
PropertiesCubic
Snark
Table of graphs and parameters

In the

undirected cubic graph
with 12 vertices and 18 edges. It is named after
Heinrich Franz Friedrich Tietze, who showed in 1910 that the Möbius strip can be subdivided into six regions that all touch each other – three along the boundary of the strip and three along its center line – and therefore that graphs that are embedded onto the Möbius strip may require six colors.[1]
The boundary segments of the regions of Tietze's subdivision (including the segments along the boundary of the Möbius strip itself) form an embedding of Tietze's graph.

Relation to Petersen graph

Tietze's graph may be formed from the Petersen graph by replacing one of its vertices with a triangle.[2][3] Like the Tietze graph, the Petersen graph forms the boundary of six mutually touching regions, but on the projective plane rather than on the Möbius strip. If one cuts a hole from this subdivision of the projective plane, surrounding a single vertex, the surrounded vertex is replaced by a triangle of region boundaries around the hole, giving the previously described construction of the Tietze graph.

Hamiltonicity

Both Tietze's graph and the Petersen graph are maximally nonhamiltonian: they have no

Hamiltonian cycle, but any two non-adjacent vertices can be connected by a Hamiltonian path.[2] Tietze's graph and the Petersen graph are the only 2-vertex-connected cubic non-Hamiltonian graphs with 12 or fewer vertices.[4]

Unlike the Petersen graph, Tietze's graph is not hypohamiltonian: removing one of its three triangle vertices forms a smaller graph that remains non-Hamiltonian.

Edge coloring and perfect matchings

Edge coloring Tietze's graph requires four colors; that is, its chromatic index is 4. Equivalently, the edges of Tietze's graph can be partitioned into four matchings, but no fewer.

Tietze's graph matches part of the definition of a

bridgeless graph that is not 3-edge-colorable. However, most authors restrict snarks to graphs without 3-cycles, so Tietze's graph is not generally considered to be a snark. Nevertheless, it is isomorphic to the graph J3, part of an infinite family of flower snarks introduced by R. Isaacs in 1975.[5]

Unlike the Petersen graph, the Tietze graph can be covered by four

NP-complete.[6]

Additional properties

Tietze's graph has chromatic number 3, chromatic index 4,

independence number is 5. Its automorphism group has order 12, and is isomorphic to the dihedral group D6, the group of symmetries of a regular hexagon (including both rotations and reflections). This group has two orbits of size 3 and one of size 6 on vertices, and thus this graph is not vertex-transitive
.

  • The chromatic number of the Tietze graph is 3.
    The
    chromatic number
    of the Tietze graph is 3.
  • The chromatic index of the Tietze graph is 4.
    The
    chromatic index
    of the Tietze graph is 4.
  • The Tietze graph has crossing number 2 and is 1-planar.
    The Tietze graph has crossing number 2 and is 1-planar.
  • A three-dimensional embedding of the Tietze graph.
    A three-dimensional embedding of the Tietze graph.
Wikimedia Commons has media related to Tietze's graph.

See also

Notes

  1. Tietze, Heinrich (1910), "Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen"
    [Some remarks on the problem of map coloring on one-sided surfaces] (PDF), DMV Annual Report, 19: 155–159
  2. ^
    S2CID 122218690
  3. ^ Weisstein, Eric W. "Tietze's Graph". MathWorld.
  4. ^ Punnim, Narong; Saenpholphat, Varaporn; Thaithae, Sermsri (2007), "Almost Hamiltonian cubic graphs" (PDF), International Journal of Computer Science and Network Security, 7 (1): 83–86
  5. JSTOR 2319844
    .
  6. S2CID 15284123
    .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Tietze%27s_graph&oldid=1242986349"