Toroidal polyhedron

Source: Wikipedia, the free encyclopedia.
A polyhedral torus can be constructed to approximate a torus surface, from a net of quadrilateral faces, like this 6x4 example.

In

topological genus (g) of 1 or greater. Notable examples include the Császár and Szilassi polyhedra
.

Variations in definition

Toroidal polyhedra are defined as collections of

link of the vertex. For toroidal polyhedra, this manifold is an orientable surface.[1] Some authors restrict the phrase "toroidal polyhedra" to mean more specifically polyhedra topologically equivalent to the (genus 1) torus.[2]

In this area, it is important to distinguish

abstract polyhedra, topological surfaces without any specified geometric realization.[3] Intermediate between these two extremes are polyhedra formed by geometric polygons or star polygons
in Euclidean space that are allowed to cross each other.

In all of these cases the toroidal nature of a polyhedron can be verified by its orientability and by its Euler characteristic being non-positive. The Euler characteristic generalizes to V − E + F = 2 − 2g, where g is its topological genus.

Császár and Szilassi polyhedra

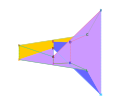Interactive Csaszar polyhedron model – in the SVG image, move the mouse left and right to rotate it.[4]
Interactive Szilassi polyhedron model – in the SVG image, move the mouse to rotate it.[5]

Two of the simplest possible embedded toroidal polyhedra are the Császár and Szilassi polyhedra.

The Császár polyhedron is a seven-vertex toroidal polyhedron with 21 edges and 14 triangular faces.[6] It and the tetrahedron are the only known polyhedra in which every possible line segment connecting two vertices forms an edge of the polyhedron.[7] Its dual, the Szilassi polyhedron, has seven hexagonal faces that are all adjacent to each other,[8] hence providing the existence half of the theorem that the maximum number of colors needed for a map on a (genus one) torus is seven.[9]

The Császár polyhedron has the fewest possible vertices of any embedded toroidal polyhedron, and the Szilassi polyhedron has the fewest possible faces of any embedded toroidal polyhedron.

Conway's toroidal deltahedron

Conway's toroidal deltahedron
Conway's toroidal deltahedron

A toroidal

coplanar. Conway suggested that it should be the deltahedral toroid with the fewest possible faces.[10]

Stewart toroids

A special category of toroidal polyhedra are constructed exclusively by

convex polyhedra; however, unlike the Johnson solids, there are infinitely many Stewart toroids.[13] They include also toroidal deltahedra
, polyhedra whose faces are all equilateral triangles.

A restricted class of Stewart toroids, also defined by Stewart, are the quasi-convex toroidal polyhedra. These are Stewart toroids that include all of the edges of their convex hulls. For such a polyhedron, each face of the convex hull either lies on the surface of the toroid, or is a polygon all of whose edges lie on the surface of the toroid.[14]

Stewart toroids by augmentation of a single polyhedron
Genus 1 1
Image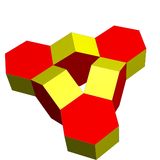
Polyhedra 6 hexagonal prisms 8
octahedra
Vertices 48 24
Edges 84 72
Faces 36 48
Quasi-convex Stewart toroids
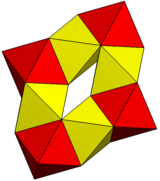
Genus 1 3 11 3 5 7 11
Image
Polyhedra 4
tetrahedra
 6 triangular cupolae
6 square pyramids 		4 triangular cupolae
6 square pyramids 		24
tetrahedra
 6 square cupolae
4 triangular cupolae
12 cubes 		8 triangular cupolae
12 cubes 		6 square cupolae
12 cubes 		6 square cupolae
8 triangular cupolae
Convex hull truncated cube truncated octahedron truncated octahedron expanded cuboctahedron truncated cuboctahedron truncated cuboctahedron truncated cuboctahedron truncated cuboctahedron
Vertices 32 30 30 62 72 72 72 72
Edges 64 60 72 168 144 168 168 168
Faces 32 30 38 86 68 88 84 76

Self-crossing polyhedra


Octahemioctahedron
Small cubicuboctahedron
Great dodecahedron

A polyhedron that is formed by a system of crossing polygons corresponds to an abstract topological manifold formed by its polygons and their system of shared edges and vertices, and the genus of the polyhedron may be determined from this abstract manifold. Examples include the genus-1 octahemioctahedron, the genus-3 small cubicuboctahedron, and the genus-4 great dodecahedron.

Crown polyhedra

dihedral symmetry and has the same vertices as the uniform pentagonal prism
.

A crown polyhedron or stephanoid is a toroidal polyhedron which is also

self-dual.[15]

See also

References

  1. ^ Whiteley (1979); Stewart (1980), p. 15.
  2. S2CID 117884274
    .
  3. MR 0621628
    .
  4. ^ Ákos Császár, A Polyhedron Without Diagonals., Bolyai Institute, University of Szeged, 1949
  5. ISSN 1715-0868
  6. ^ Császár, A. (1949), "A polyhedron without diagonals", Acta Sci. Math. Szeged, 13: 140–142.
  7. S2CID 15911143
    .
  8. ^ Szilassi, Lajos (1986), "Regular toroids" (PDF), Structural Topology, 13: 69–80[permanent dead link].
  9. ^ Heawood, P. J. (1890), "Map colouring theorems", Quarterly Journal of Mathematics, First Series, 24: 322–339
  10. ^ Conway, John, "Polyhedra of positive genus", geometry.research Usenet group; see messages dated "Sep 23, 1997, 12:00:00 AM" announcing the toroidal deltahedron, and "Sep 25, 1997, 12:00:00 AM" describing its construction. Unlike the § Stewart toroids, it has coplanar adjacent triangles, but otherwise resembles a toroidal deltahedron with more faces described by Stewart (1980), p. 60.
  11. MR 2001419
    .
  12. ISBN 978-0-686-11936-4
    .
  13. ^ Stewart (1980), p. 15.
  14. ^ Stewart (1980), "Quasi-convexity and weak quasi-convexity", pp. 76–79.
  15. doi:10.1007/978-94-011-0924-6_3. See in particular p. 60
    .

External links
Retrieved from "https://en.wikipedia.org/w/index.php?title=Toroidal_polyhedron&oldid=1220120903"