Квазиправильный многогранник

Квазипра́вильный многогра́нник (от лат. quas(i) «наподобие», «нечто вроде») — полуправильный многогранник, который имеет в точности два вида правильных граней, поочерёдно следующих вокруг каждой вершины. Эти многогранники рёберно транзитивны^[англ.], а потому на шаг ближе к правильным многогранникам, чем полуправильные, которые лишь вершинно транзитивны.

Квазиправильные фигуры

(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.∞)2
${\displaystyle {\begin{Bmatrix}3\\3\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}3\\4\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}3\\5\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}3\\6\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}3\\7\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}3\\8\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}3\\\infty \end{Bmatrix}}}$
r{3,3}	r{3,4}	r{3,5}	r{3,6}	r{3,7}[англ.]	r{3,8}[англ.]	r{3,∞}[англ.]
Квазиправильные многогранники или мозаики имеют в точности два типа правильных граней, которые располагаются поочерёдно вокруг каждой вершины. Их вершинные фигуры являются прямоугольниками .

Существует только два

Эти формы, представленные парой (правильным многогранником и двойственным ему), могут быть заданы вертикальным символом Шлефли ${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$ или r{p, q} для представления граней как правильного {p, q}, так и двойственного {q, p} многогранников. Квазиправильный многогранник с этим символом имеет вершинную конфигурацию^[англ.] p.q.p.q (или (p.q)²).

В более общем случае квазиправильные фигуры могут иметь вершинную конфигурацию^[англ.] (p.q)^r, представляющую r (2 или более) граней разного вида вокруг вершины.

Некоторые правильные многогранники и мозаики (имеющие чётное число граней в каждой вершине) могут также рассматриваться как квазиправильные путём разделения граней на два множества (как если бы мы их выкрасили в разные цвета). Правильная фигура с символом Шлефли {p, q} может быть квазиправильной и будет иметь вершинную кофигурацию (p.p)^q/2, если q чётно.

Правильные и квазиправильные фигуры

Прямоугольные треугольники (p p 2)[1]
{3,4} r{3,3}	{4,4} r{4,4}	{5,4} r{5,5}	{6,4} r{6,6}	{7,4} r{7,7}	{8,4} r{8,8}	{∞,4} r{∞,∞}
${\displaystyle {\begin{Bmatrix}3\\3\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}4\\4\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}5\\5\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}6\\6\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}7\\7\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}8\\8\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}\infty \\\infty \end{Bmatrix}}}$
(3.3)2	(4.4)2	(5.5)2[англ.]	(6.6)2[англ.]	(7.7)2[англ.]	(8.8)2[англ.]	(∞.∞)2[англ.]
	Квадратный паркет	5-угольная мозаика 4-го порядка[англ.]	6-угольная мозаика 4-го порядка[англ.]	7-угольная мозаика 4-го порядка[англ.]	8-угольная мозаика 4-го порядка[англ.]	∞-угольная мозаика 4-го порядка[англ.]
Треугольники общего вида (p p 3)[2]
{3,6}	{4,6}[англ.]	{5,6}[англ.]	{6,6}[англ.]	{7,6}[англ.]	{8,6}[англ.]	{∞,6}[англ.]
(3.3)3	(4.4)3	(5.5)3	(6.6)3	(7.7)3	(8.8)3	(∞.∞)3
Треугольники общего вида (p p 4)
{3,8}[англ.]	{4,8}[англ.]	{5,8}[англ.]	{6,8}[англ.]	{7,8}[англ.]	{8,8}[англ.]	{∞,8}[англ.]
(3.3)4	(4.4)4	(5.5)4	(6.6)4	(7.7)4	(8.8)4	(∞.∞)4
Правильный многогранник или мозаика могут считаться квазиправильными, если они имеют чётное число граней при каждой вершине (а потому могут быть выкрашены в два цвета, чтобы соседние грани имели разные цвета).

Правильные (p | 2 q) и квазиправильные многогранники (2 | p q) получаются построением Витхоффа с генераторной точкой на одном из 3 углов фундаментальной области. Это задаёт единственное ребро внутри фундаментальной области.

Коксетер определяет квазиправильный многогранник как многогранник, имеющий Символ Витхоффа^[англ.] вида p | q r, и он будет правильным, если q=2 или q=r ^[3].

Диаграммы Коксетера — Дынкина является другой формой символического представления, которое позволяет показать связь между двумя двойственно-правильными формами:

Символ Шлефли		Диаграммы Коксетера — Дынкина	Символ Витхоффа[англ.]
${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$	{p, q}		q | 2 p
${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$	{q, p}		p | 2 q
${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	r{p, q}		2 | p q

Существует два выпуклых квазиправильных многогранника:

1. Кубооктаэдр ${\displaystyle {\begin{Bmatrix}3\\4\end{Bmatrix}}}$, вершинная конфигурация (3.4)²,
   диаграмма Коксетера — Дынкина
   
2. Икосододекаэдр ${\displaystyle {\begin{Bmatrix}3\\5\end{Bmatrix}}}$, вершинная конфигурация (3.5)², диаграмма Коксетера — Дынкина

Кроме того, октаэдр, являющийся также правильным, ${\displaystyle {\begin{Bmatrix}3\\3\end{Bmatrix}}}$, с вершинной конфигурацией (3.3)², может также считаться квазиправильным, если соседним граням дать различные цвета. В таком виде его иногда называют тетратетраэдром. Оставшиеся выпуклые правильные многогранники имеют нечётное число граней при каждой вершине и не могут быть выкрашены так, чтобы обеспечить транзитивность рёбер. Тетратетраэдр имеет диаграмму Коксетера — Дынкина .

Каждый из них образует общее ядро двойственной пары

, и при таком способе получения обычно называют его тетратетраэдром.

Правильный	Двойственный правильный	Квазиправильный	Вершинная фигура
Тетраэдр {3,3} 3 | 2 3	Тетраэдр {3,3} 3 | 2 3	Тетратетраэдр r{3,3} 2 | 3 3	3.3.3.3
Куб {4,3} 3 | 2 4	Октаэдр {3,4} 4 | 2 3	Кубооктаэдр r{3,4} 2 | 3 4	3.4.3.4
Додекаэдр {5,3} 3 | 2 5	Икосаэдр {3,5} 5 | 2 3	Икосододекаэдр r{3,4} 2 | 3 5	3.5.3.5

Каждый из этих квазиправильных многогранников можно построить с помощью полного усечения любого из родителей, усекая рёбра полностью, пока они не превратятся в точки.

Эту последовательность продолжает

.

Правильный многоугольник	Двойственный правильный	Квазиправильный	Вершинная фигура
шестиугольная мозаика {6,3} 6 | 2 3	треугольная мозаика {3,6} 3 | 2 6	тришестиугольная мозаика r{5,3} 2 | 3 6	3.6.3.6

Рисунок шахматной доски является квазиправильной раскраской

вершинной фигурой

4.4.4.4:

Правильный многоугольник	Двойственный правильный	Квазиправильный	Вершинная фигура
{4,4} 4 | 2 4	{4,4} 4 | 2 4	r{4,4} 2 | 4 4	4.4.4.4

Треугольную мозаику можно также считать квазиправильной, с тремя множествами альтернированных треугольников в каждой вершине, (3.3)³:

h{6,3} 3 | 3 3 =

На гиперболической плоскости (

Правильный многоугольник	Двойственный правильный	Квазиправильный	Вершинная фигура
Семиугольная мозаика {7,3} 7 | 2 3	Треугольный паркет {3,7} 3 | 2 7	Трисемиугольная мозаика[англ.] r{3,7} 2 | 3 7	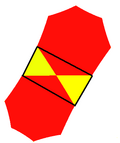3.7.3.7

Коксетер и др. (1954) классифицировали также некоторые звёздчатые многогранники, имеющие квазиправильные характеристики:

Два многогранника основываются на двойственных парах правильных тел Кеплера — Пуансо.

Большой икосододекаэдр ${\displaystyle {\begin{Bmatrix}3\\5/2\end{Bmatrix}}}$ и додекододекаэдр ${\displaystyle {\begin{Bmatrix}5\\5/2\end{Bmatrix}}}$:

Правильный	Двойственный правильный	Квазиправильный	Вершинная фигура
Большой звёздчатый додекаэдр {5/2,3} 3 | 2 5/2	Большой икосаэдр {3,5/2} 5/2 | 2 3	Большой икосододекаэдр r{3,5/2} 2 | 3 5/2	3.5/2.3.5/2
Малый звёздчатый додекаэдр {5/2,5} 5 | 2 5/2	Большой додекаэдр {5,5/2} 5/2 | 2 5	Додекододекаэдр r{5,5/2} 2 | 5 5/2	5.5/2.5.5/2

Наконец, существует три битригональных^[англ.] вида, вершинные фигуры которых содержат три перемежающихся типа граней:

Рисунок	Название многогранника Символ Витхоффа[англ.] Диаграмма Коксетера	Вершинная фигура
	Битреугольный додекододекаэдр[англ.] 3 | 5/3 5 or	(5.5/3)3
	Малый битреугольный икосододекаэдр[англ.] 3 | 5/2 3 or	(3.5/2)3
	Большой битреугольный икосододекаэдр[англ.] 3/2 | 3 5 or	((3.5)3)/2

Некоторые авторы высказывают мнение, что, поскольку двойственные многогранники к квазиправильным имеют те же симметрии, эти двойственные тела тоже следует считать квазиправильными, но не все математики придерживаются такого мнения. Эти двойственные многогранники транзитивны относительно своих рёбер и граней (но не вершин). Они являются рёберно транзитивными телами Каталана^[англ.]. Выпуклые формы, согласно порядку многогранника (как выше):

1. Ромбододекаэдр с двумя типами перемежающихся вершин, 8 вершин с тремя ромбическими гранями, и 6 вершин с четырьмя ромбическими гранями.
2. Ромботриаконтаэдр с двумя типами перемежающихся вершин, 20 вершин с тремя ромбическими гранями, и 12 вершин с пятью ромбическими гранями.

Кроме того, будучи двойственным октаэдру, куб, являющийся правильным, может быть сделан квазиправильным, если раскрасить его вершины в два цвета, так, чтобы вершины на одном ребре имели разные цвета.

Их

Куб V(3.3)2	Ромбододекаэдр V(3.4)2	Ромботри- аконтаэдр V(3.5)2	Ромбическая мозаика V(3.6)2	V(3.7)2	V(3.8)2

Эти три квазиправильных двойственных многогранника характерны наличием ромбических граней.

Эта ромбическая структура граней продолжает V(3.6)², ромбическая мозаика.

В евклидовом 4-мерном пространстве правильный

Единственные квазиправильные соты в евклидовом 3-мерном пространстве —

ячеек. Их вершинные фигуры являются квазиправильными кубооктаэдрами, ^[4]

вершинная фигура — квазиправильный треугольный паркет

, =

ячеек. Вершинная фигура — квазиправильный икосододекаэдр, . Связанные паракомпактные альтернированные кубические соты 6-го порядка^[англ.], h{4,3,6} имеют альтернированные тетраэдральные и шестиугольные мозаичные ячейки с вершинной фигурой, которая является тришестиугольной мозаикой

, .

Квазиправильные многогранники и соты: h{4,p,q}

Пространство	Конечное	Аффинное	Компактное	Паракомпактное
Название	h{4,3,3}	h{4,3,4}	h{4,3,5}	h{4,3,6}	h{4,4,3}	h{4,4,4}
	${\displaystyle \left\{3,{3 \atop 3}\right\}}$	${\displaystyle \left\{3,{3 \atop 4}\right\}}$	${\displaystyle \left\{3,{3 \atop 5}\right\}}$	${\displaystyle \left\{3,{3 \atop 6}\right\}}$	${\displaystyle \left\{4,{3 \atop 4}\right\}}$	${\displaystyle \left\{4,{4 \atop 4}\right\}}$
Диаграмма Коксетера
Рисунок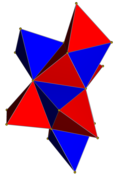
Вершинная фигура r{p,3}

Можно уменьшить симметрию правильных многогранных сот вида {p,3,4} или как и получить квазиправильный вид , создавая попеременную раскраску {p,3} ячеек. Это можно сделать для евклидовых

вершинные фигуры

 — квазиправильные тетраэдры, = .

Правильные и квазиправильные соты: {p,3,4} и {p,3^1,1}

Пространство	Евклидово 4-мерное	Евклидово 3-мерное	Гиперболическое 3-мерное
Название	{3,3,4} {3,31,1} = ${\displaystyle \left\{3,{3 \atop 3}\right\}}$	{4,3,4} {4,31,1} = ${\displaystyle \left\{4,{3 \atop 3}\right\}}$	{5,3,4} {5,31,1} = ${\displaystyle \left\{5,{3 \atop 3}\right\}}$	{6,3,4} {6,31,1} = ${\displaystyle \left\{6,{3 \atop 3}\right\}}$
Диаграмма Коксетера	=	=	=	=
Рисунок
Ячейки {p,3}

Таким же образом можно уменьшить вдвое симметрию правильных гиперболических сот вида {p,3,6} или как и получить квазиправильный вид , задавая попеременную раскраску {p,3} ячеек. Они имеют шесть ячеек вокруг каждого ребра, поочерёдно выкрашенные в 2 цвета. Их

, .

Гиперболические однородные соты: {p,3,6} и {p,3^[3]}

Вид	Паракомпактные				Некомпактные
Название	{3,3,6} {3,3[3]}	{4,3,6} {4,3[3]}	{5,3,6} {5,3[3]}	{6,3,6} {6,3[3]}	{7,3,6} {7,3[3]}	{8,3,6} {8,3[3]}	... {∞,3,6} {∞,3[3]}
Рисунок
Ячейки	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

См. также

• Хиральный многогранник
• Полное усечение (геометрия)

• Weisstein, Eric W. Quasiregular polyhedron (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Uniform polyhedron (англ.) на сайте Wolfram MathWorld. Quasi-regular polyhedra: (p.q)^r
• George Hart, Quasiregular polyhedra Архивировано 2 сентября 2013 года.

У этой статьи есть несколько проблем, помогите их исправить: Необходимо проверить качество перевода c неуказанного языка, исправить содержательные и стилистические ошибки. Вы можете помочь улучшить эту статью (см. также рекомендации по переводу). Оригинал не указан. Пожалуйста, укажите его. (27 ноября 2015) Стиль этой статьи неэнциклопедичен или нарушает нормы литературного русского языка. Статью следует исправить согласно стилистическим правилам Википедии. (27 ноября 2015) Пожалуйста, после исправления проблемы исключите её из списка параметров. После устранения всех недостатков этот шаблон может быть удалён любым участником.