Radial velocity

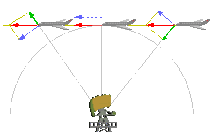
The radial velocity or line-of-sight velocity of a target with respect to an observer is the

Let the instantaneous relative velocity of the target with respect to the observer be

${\displaystyle {\vec {v}}={\frac {d{\vec {r}}}{dt}}\in \mathbb {R} ^{3}}$

(1)

The magnitude of the position vector ${\displaystyle {\vec {r}}}$ is defined as in terms of the

${\displaystyle r=\|{\vec {r}}\|=\langle {\vec {r}},{\vec {r}}\rangle ^{1/2}}$

(2)

The quantity range rate is the time derivative of the magnitude (norm) of ${\displaystyle {\vec {r}}}$, expressed as

${\displaystyle {\dot {r}}={\frac {dr}{dt}}}$

(3)

Substituting (2) into (3)

${\displaystyle {\dot {r}}={\frac {d\langle {\vec {r}},{\vec {r}}\rangle ^{1/2}}{dt}}}$

Evaluating the derivative of the right-hand-side by the chain rule

${\displaystyle {\dot {r}}={\frac {1}{2}}{\frac {d\langle {\vec {r}},{\vec {r}}\rangle }{dt}}{\frac {1}{r}}}$

${\displaystyle {\dot {r}}={\frac {1}{2}}{\frac {\langle {\frac {d{\vec {r}}}{dt}},{\vec {r}}\rangle +\langle {\vec {r}},{\frac {d{\vec {r}}}{dt}}\rangle }{r}}}$

using (1) the expression becomes

${\displaystyle {\dot {r}}={\frac {1}{2}}{\frac {\langle {\vec {v}},{\vec {r}}\rangle +\langle {\vec {r}},{\vec {v}}\rangle }{r}}}$

By reciprocity,^[1] ${\displaystyle \langle {\vec {v}},{\vec {r}}\rangle =\langle {\vec {r}},{\vec {v}}\rangle }$. Defining the unit relative position vector ${\displaystyle {\hat {r}}={\vec {r}}/{r}}$ (or LOS direction), the range rate is simply expressed as

${\displaystyle {\dot {r}}={\frac {\langle {\vec {r}},{\vec {v}}\rangle }{r}}=\langle {\hat {r}},{\vec {v}}\rangle }$

i.e., the projection of the relative velocity vector onto the LOS direction.

Further defining the velocity direction ${\displaystyle {\hat {v}}={\vec {v}}/{v}}$, with the

${\displaystyle v=\|{\vec {v}}\|}$

${\displaystyle {\dot {r}}=v\langle {\hat {r}},{\hat {v}}\rangle =v\langle {\hat {r}},{\hat {v}}\rangle }$

where the inner product is either +1 or -1, for parallel and

A singularity exists for coincident observer target, i.e., ${\displaystyle r=0}$; in this case, range rate is undefined.

Applications in astronomy

In astronomy, radial velocity is often measured to the first order of approximation by

The radial velocity of a star or other luminous distant objects can be measured accurately by taking a high-resolution spectrum and comparing the measured wavelengths of known spectral lines to wavelengths from laboratory measurements. A positive radial velocity indicates the distance between the objects is or was increasing; a negative radial velocity indicates the distance between the source and observer is or was decreasing.

William Huggins ventured in 1868 to estimate the radial velocity of Sirius with respect to the Sun, based on observed redshift of the star's light.^[6]

In many

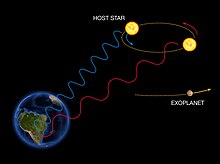
The radial velocity method to detect exoplanets is based on the detection of variations in the velocity of the central star, due to the changing direction of the gravitational pull from an (unseen) exoplanet as it orbits the star. When the star moves towards us, its spectrum is blueshifted, while it is redshifted when it moves away from us. By regularly looking at the spectrum of a star—and so, measuring its velocity—it can be determined if it moves periodically due to the influence of an exoplanet companion.

Data reduction

From the instrumental perspective, velocities are measured relative to the telescope's motion. So an important first step of the data reduction is to remove the contributions of

• the Earth's elliptic motion around the Sun at approximately ± 30 km/s,
• a monthly rotation of ± 13 m/s of the Earth around the center of gravity of the Earth-Moon system,^[9]
• the daily rotation of the telescope with the Earth crust around the Earth axis, which is up to ±460 m/s at the equator and proportional to the cosine of the telescope's geographic latitude,
• small contributions from the Earth polar motion at the level of mm/s,
• contributions of 230 km/s from the motion around the Galactic Center and associated proper motions.^[10]
• in the case of spectroscopic measurements corrections of the order of ±20 cm/s with respect to aberration.^[11]
• Sin i degeneracy
  is the impact caused by not being in the plane of the motion.

See also

• Proper motion – Measure of observed changes in the apparent locations of stars
• Peculiar velocity – Velocity of an object relative to a rest frame
• Relative velocity – Velocity of an object or observer in the rest frame of another object or observer
• Space velocity (astronomy)
   – Study of the movement of starsPages displaying short descriptions of redirect targets
• Bistatic range rate
• Doppler effect
• Inner product
• Orbit determination
• Lp space

Notes