Absolute value

In mathematics, the absolute value or modulus of a real number ${\displaystyle x}$, denoted ${\displaystyle |x|}$, is the

value of ${\displaystyle x}$ without regard to its sign. Namely, ${\displaystyle |x|=x}$ if ${\displaystyle x}$ is a , and ${\displaystyle |x|=-x}$ if ${\displaystyle x}$ is negative (in which case negating ${\displaystyle x}$ makes ${\displaystyle -x}$ positive), and ${\displaystyle |0|=0}$. For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its distance from zero.

Generalisations of the absolute value for real numbers occur in a wide variety of mathematical settings. For example, an absolute value is also defined for the complex numbers, the quaternions, ordered rings, fields and vector spaces. The absolute value is closely related to the notions of magnitude, distance, and norm in various mathematical and physical contexts.

In 1806, Jean-Robert Argand introduced the term module, meaning unit of measure in French, specifically for the complex absolute value,^[1][2] and it was borrowed into English in 1866 as the Latin equivalent modulus.^[1] The term absolute value has been used in this sense from at least 1806 in French^[3] and 1857 in English.^[4] The notation |x|, with a vertical bar on each side, was introduced by Karl Weierstrass in 1841.^[5] Other names for absolute value include numerical value^[1] and magnitude.^[1] The absolute value of ${\displaystyle x}$ has also been denoted ${\displaystyle \operatorname {abs} x}$ in some mathematical publications,^[6] and in spreadsheets, programming languages, and computational software packages, the absolute value of ${\textstyle x}$ is generally represented by abs(x), or a similar expression,^[7] as it has been since the earliest days of high-level programming languages.^[8]

The vertical bar notation also appears in a number of other mathematical contexts: for example, when applied to a set, it denotes its

of a vector in ${\displaystyle \mathbb {R} ^{n}}$, although double vertical bars with subscripts (${\displaystyle \|\cdot \|_{2}}$ and ${\displaystyle \|\cdot \|_{\infty }}$, respectively) are a more common and less ambiguous notation.

Definition and properties

Real numbers

For any real number ${\displaystyle x}$, the absolute value or modulus of ${\displaystyle x}$ is denoted by ${\displaystyle |x|}$, with a vertical bar on each side of the quantity, and is defined as^[12] $${\displaystyle |x|={\begin{cases}x,&{\text{if }}x\geq 0\\-x,&{\text{if }}x<0.\end{cases}}}$$

The absolute value of ${\displaystyle x}$ is thus always either a

. When ${\displaystyle x}$ itself is negative (${\displaystyle x<0}$), then its absolute value is necessarily positive (${\displaystyle |x|=-x>0}$).

From an

below).

Since the square root symbol represents the unique positive square root, when applied to a positive number, it follows that $${\displaystyle |x|={\sqrt {x^{2}}}.}$$ This is equivalent to the definition above, and may be used as an alternative definition of the absolute value of real numbers.^[14]

The absolute value has the following four fundamental properties (${\textstyle a}$, ${\textstyle b}$ are real numbers), that are used for generalization of this notion to other domains:

${\displaystyle |a|\geq 0}$	Non-negativity
${\displaystyle |a|=0\iff a=0}$	Positive-definiteness
${\displaystyle |ab|=\left|a\right|\left|b\right|}$	Multiplicativity
${\displaystyle |a+b|\leq |a|+|b|}$	Subadditivity, specifically the triangle inequality

Non-negativity, positive definiteness, and multiplicativity are readily apparent from the definition. To see that subadditivity holds, first note that ${\displaystyle |a+b|=s(a+b)}$ where ${\displaystyle s=\pm 1}$, with its sign chosen to make the result positive. Now, since ${\displaystyle -1\cdot x\leq |x|}$ and ${\displaystyle +1\cdot x\leq |x|}$, it follows that, whichever of ${\displaystyle \pm 1}$ is the value of ${\displaystyle s}$, one has ${\displaystyle s\cdot x\leq |x|}$ for all real ${\displaystyle x}$. Consequently, ${\displaystyle |a+b|=s\cdot (a+b)=s\cdot a+s\cdot b\leq |a|+|b|}$, as desired.

Some additional useful properties are given below. These are either immediate consequences of the definition or implied by the four fundamental properties above.

${\displaystyle {\bigl |}\left|a\right|{\bigr |}=|a|}$	Idempotence (the absolute value of the absolute value is the absolute value)
${\displaystyle \left|-a\right|=|a|}$	Evenness (reflection symmetry of the graph)
${\displaystyle |a-b|=0\iff a=b}$	Identity of indiscernibles (equivalent to positive-definiteness)
${\displaystyle |a-b|\leq |a-c|+|c-b|}$	Triangle inequality (equivalent to subadditivity)
${\displaystyle \left|{\frac {a}{b}}\right|={\frac {|a|}{|b|}}\ }$ (if ${\displaystyle b\neq 0}$)	Preservation of division (equivalent to multiplicativity)
${\displaystyle |a-b|\geq {\bigl |}\left|a\right|-\left|b\right|{\bigr |}}$	Reverse triangle inequality (equivalent to subadditivity)

Two other useful properties concerning inequalities are:

${\displaystyle |a|\leq b\iff -b\leq a\leq b}$

${\displaystyle |a|\geq b\iff a\leq -b\ }$ or ${\displaystyle a\geq b}$

These relations may be used to solve inequalities involving absolute values. For example:

${\displaystyle |x-3|\leq 9}$	${\displaystyle \iff -9\leq x-3\leq 9}$
	${\displaystyle \iff -6\leq x\leq 12}$

The absolute value, as "distance from zero", is used to define the absolute difference between arbitrary real numbers, the standard

on the real numbers.

Since the

: for any complex number $${\displaystyle z=x+iy,}$$ where ${\displaystyle x}$ and ${\displaystyle y}$ are real numbers, the absolute value or modulus of ${\displaystyle z}$ is denoted ${\displaystyle |z|}$ and is defined by[15] $${\displaystyle |z|={\sqrt {\operatorname {Re} (z)^{2}+\operatorname {Im} (z)^{2}}}={\sqrt {x^{2}+y^{2}}},}$$ the Pythagorean addition of ${\displaystyle x}$ and ${\displaystyle y}$, where ${\displaystyle \operatorname {Re} (z)=x}$ and ${\displaystyle \operatorname {Im} (z)=y}$ denote the real and imaginary parts of ${\displaystyle z}$, respectively. When the imaginary part ${\displaystyle y}$ is zero, this coincides with the definition of the absolute value of the real number ${\displaystyle x}$.

When a complex number ${\displaystyle z}$ is expressed in its polar form as ${\displaystyle z=re^{i\theta },}$ its absolute value is ${\displaystyle |z|=r.}$

Since the product of any complex number ${\displaystyle z}$ and its complex conjugate ${\displaystyle {\bar {z}}=x-iy}$, with the same absolute value, is always the non-negative real number ${\displaystyle \left(x^{2}+y^{2}\right)}$, the absolute value of a complex number ${\displaystyle z}$ is the square root of ${\displaystyle z\cdot {\overline {z}},}$ which is therefore called the

or squared modulus of ${\displaystyle z}$: $${\displaystyle |z|={\sqrt {z\cdot {\overline {z}}}}.}$$ This generalizes the alternative definition for reals: ${\textstyle |x|={\sqrt {x\cdot x}}}$.

The complex absolute value shares the four fundamental properties given above for the real absolute value. The identity ${\displaystyle |z|^{2}=|z^{2}|}$ is a special case of multiplicativity that is often useful by itself.

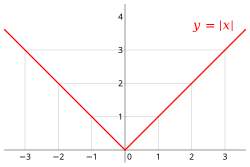
Composition of absolute value with a cubic function

in different orders

The real absolute value function is

.

For both real and complex numbers the absolute value function is

idempotent

(meaning that the absolute value of any absolute value is itself).

Relationship to the sign function

The absolute value function of a real number returns its value irrespective of its sign, whereas the sign (or signum) function returns a number's sign irrespective of its value. The following equations show the relationship between these two functions:

${\displaystyle |x|=x\operatorname {sgn}(x),}$

or

${\displaystyle |x|\operatorname {sgn}(x)=x,}$

and for x ≠ 0,

${\displaystyle \operatorname {sgn}(x)={\frac {|x|}{x}}={\frac {x}{|x|}}.}$

Let ${\displaystyle s,t\in \mathbb {R} }$, then the following relationship to the

functions hold:

${\displaystyle |t-s|=-2\min(s,t)+s+t}$

and

${\displaystyle |t-s|=2\max(s,t)-s-t.}$

The formulas can be derived by considering each case ${\displaystyle s>t}$ and ${\displaystyle t>s}$ separately.

From the last formula one can derive also ${\displaystyle |t|=\max(t,-t)}$.

The real absolute value function has a

${\displaystyle {\frac {d\left|x\right|}{dx}}={\frac {x}{|x|}}={\begin{cases}-1&x<0\\1&x>0.\end{cases}}}$

The real absolute value function is an example of a continuous function that achieves a global minimum where the derivative does not exist.

The subdifferential of |x| at x = 0 is the interval [−1, 1].^[18]

The

The second derivative of |x| with respect to x is zero everywhere except zero, where it does not exist. As a

.

Antiderivative

The antiderivative (indefinite integral) of the real absolute value function is

${\displaystyle \int \left|x\right|dx={\frac {x\left|x\right|}{2}}+C,}$

where C is an arbitrary

) functions, which the complex absolute value function is not.

The following two formulae are special cases of the chain rule:

${\displaystyle {d \over dx}f(|x|)={x \over |x|}(f'(|x|))}$

if the absolute value is inside a function, and

${\displaystyle {d \over dx}|f(x)|={f(x) \over |f(x)|}f'(x)}$

if another function is inside the absolute value. In the first case, the derivative is always discontinuous at ${\textstyle x=0}$ in the first case and where ${\textstyle f(x)=0}$ in the second case.

The absolute value is closely related to the idea of distance. As noted above, the absolute value of a real or complex number is the distance from that number to the origin, along the real number line, for real numbers, or in the complex plane, for complex numbers, and more generally, the absolute value of the difference of two real or complex numbers is the distance between them.

The standard Euclidean distance between two points

${\displaystyle a=(a_{1},a_{2},\dots ,a_{n})}$

and

${\displaystyle b=(b_{1},b_{2},\dots ,b_{n})}$

in Euclidean n-space is defined as:

${\displaystyle {\sqrt {\textstyle \sum _{i=1}^{n}(a_{i}-b_{i})^{2}}}.}$

This can be seen as a generalisation, since for ${\displaystyle a_{1}}$ and ${\displaystyle b_{1}}$ real, i.e. in a 1-space, according to the alternative definition of the absolute value,

${\displaystyle |a_{1}-b_{1}|={\sqrt {(a_{1}-b_{1})^{2}}}={\sqrt {\textstyle \sum _{i=1}^{1}(a_{i}-b_{i})^{2}}},}$

and for ${\displaystyle a=a_{1}+ia_{2}}$ and ${\displaystyle b=b_{1}+ib_{2}}$ complex numbers, i.e. in a 2-space,

${\displaystyle |a-b|}$	${\displaystyle =|(a_{1}+ia_{2})-(b_{1}+ib_{2})|}$
	${\displaystyle =|(a_{1}-b_{1})+i(a_{2}-b_{2})|}$
	${\displaystyle ={\sqrt {(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}}}={\sqrt {\textstyle \sum _{i=1}^{2}(a_{i}-b_{i})^{2}}}.}$

The above shows that the "absolute value"-distance, for real and complex numbers, agrees with the standard Euclidean distance, which they inherit as a result of considering them as one and two-dimensional Euclidean spaces, respectively.

The properties of the absolute value of the difference of two real or complex numbers: non-negativity, identity of indiscernibles, symmetry and the triangle inequality given above, can be seen to motivate the more general notion of a

as follows:

A real valued function d on a set X × X is called a

${\displaystyle d(a,b)\geq 0}$	Non-negativity
${\displaystyle d(a,b)=0\iff a=b}$	Identity of indiscernibles
${\displaystyle d(a,b)=d(b,a)}$	Symmetry
${\displaystyle d(a,b)\leq d(a,c)+d(c,b)}$	Triangle inequality

Generalizations

Ordered rings

The definition of absolute value given for real numbers above can be extended to any ordered ring. That is, if a is an element of an ordered ring R, then the absolute value of a, denoted by |a|, is defined to be:^[20]

${\displaystyle |a|=\left\{{\begin{array}{rl}a,&{\text{if }}a\geq 0\\-a,&{\text{if }}a<0.\end{array}}\right.}$

where −a is the additive inverse of a, 0 is the additive identity, and < and ≥ have the usual meaning with respect to the ordering in the ring.

The four fundamental properties of the absolute value for real numbers can be used to generalise the notion of absolute value to an arbitrary field, as follows.

A real-valued function v on a field F is called an absolute value (also a modulus, magnitude, value, or valuation)^[21] if it satisfies the following four axioms:

${\displaystyle v(a)\geq 0}$	Non-negativity
${\displaystyle v(a)=0\iff a=\mathbf {0} }$	Positive-definiteness
${\displaystyle v(ab)=v(a)v(b)}$	Multiplicativity
${\displaystyle v(a+b)\leq v(a)+v(b)}$	Subadditivity or the triangle inequality

Where 0 denotes the

of F. The real and complex absolute values defined above are examples of absolute values for an arbitrary field.

If v is an absolute value on F, then the function d on F × F, defined by d(a, b) = v(a − b), is a metric and the following are equivalent:

• d satisfies the
  ultrametric
  inequality ${\displaystyle d(x,y)\leq \max(d(x,z),d(y,z))}$ for all x, y, z in F.
• ${\textstyle \left\{v\left(\sum _{k=1}^{n}\mathbf {1} \right):n\in \mathbb {N} \right\}}$ is bounded in R.
• ${\displaystyle v\left({\textstyle \sum _{k=1}^{n}}\mathbf {1} \right)\leq 1\ }$ for every ${\displaystyle n\in \mathbb {N} }$.
• ${\displaystyle v(a)\leq 1\Rightarrow v(1+a)\leq 1\ }$ for all ${\displaystyle a\in F}$.
• ${\displaystyle v(a+b)\leq \max\{v(a),v(b)\}\ }$ for all ${\displaystyle a,b\in F}$.

An absolute value which satisfies any (hence all) of the above conditions is said to be non-Archimedean, otherwise it is said to be

Vector spaces

Again the fundamental properties of the absolute value for real numbers can be used, with a slight modification, to generalise the notion to an arbitrary vector space.

A real-valued function on a vector space V over a field F, represented as ‖ · ‖, is called an absolute value, but more usually a norm, if it satisfies the following axioms:

For all a in F, and v, u in V,

${\displaystyle \|\mathbf {v} \|\geq 0}$	Non-negativity
${\displaystyle \|\mathbf {v} \|=0\iff \mathbf {v} =0}$	Positive-definiteness
${\displaystyle \|a\mathbf {v} \|=\left|a\right|\left\|\mathbf {v} \right\|}$	Absolute homogeneity or positive scalability
${\displaystyle \|\mathbf {v} +\mathbf {u} \|\leq \|\mathbf {v} \|+\|\mathbf {u} \|}$	Subadditivity or the triangle inequality

The norm of a vector is also called its length or magnitude.

In the case of Euclidean space ${\displaystyle \mathbb {R} ^{n}}$, the function defined by

${\displaystyle \|(x_{1},x_{2},\dots ,x_{n})\|={\sqrt {\textstyle \sum _{i=1}^{n}x_{i}^{2}}}}$

is a norm called the Euclidean norm. When the real numbers ${\displaystyle \mathbb {R} }$ are considered as the one-dimensional vector space ${\displaystyle \mathbb {R} ^{1}}$, the absolute value is a

) for any p. In fact the absolute value is the "only" norm on ${\displaystyle \mathbb {R} ^{1}}$, in the sense that, for every norm ‖ · ‖ on ${\displaystyle \mathbb {R} ^{1}}$, ‖x‖ = ‖1‖ ⋅ |x|.

The complex absolute value is a special case of the norm in an inner product space, which is identical to the Euclidean norm when the complex plane is identified as the Euclidean plane ${\displaystyle \mathbb {R} ^{2}}$.

Every composition algebra A has an involution x → x* called its conjugation. The product in A of an element x and its conjugate x* is written N(x) = x x* and called the norm of x.

The real numbers ${\displaystyle \mathbb {R} }$, complex numbers ${\displaystyle \mathbb {C} }$, and quaternions ${\displaystyle \mathbb {H} }$ are all composition algebras with norms given by definite quadratic forms. The absolute value in these division algebras is given by the square root of the composition algebra norm.

In general the norm of a composition algebra may be a quadratic form that is not definite and has null vectors. However, as in the case of division algebras, when an element x has a non-zero norm, then x has a multiplicative inverse given by x*/N(x).

• Least absolute values

References

• Bartle; Sherbert; Introduction to real analysis (4th ed.), John Wiley & Sons, 2011
  ISBN 978-0-471-43331-6
  .
• Nahin, Paul J.; An Imaginary Tale; Princeton University Press; (hardcover, 1998).
  ISBN 0-691-02795-1
  .
• Mac Lane, Saunders, Garrett Birkhoff, Algebra, American Mathematical Soc., 1999.
  ISBN 978-0-8218-1646-2
  .
• Mendelson, Elliott, Schaum's Outline of Beginning Calculus, McGraw-Hill Professional, 2008.
  ISBN 978-0-07-148754-2
  .
• O'Connor, J.J. and Robertson, E.F.; "Jean Robert Argand".
• Schechter, Eric; Handbook of Analysis and Its Foundations, pp. 259–263, "Absolute Values", Academic Press (1997)
  ISBN 0-12-622760-8
  .

External links

• "Absolute value". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
• absolute value at PlanetMath.
• Weisstein, Eric W. "Absolute Value". MathWorld.