Allen–Cahn equation

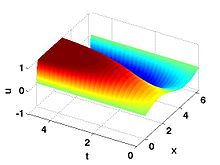
The Allen–Cahn equation (after

The equation describes the time evolution of a scalar-valued state variable ${\displaystyle \eta }$ on a domain ${\displaystyle \Omega }$ during a time interval ${\displaystyle {\mathcal {T}}}$, and is given by:[1]^[2]

${\displaystyle {{\partial \eta } \over {\partial t}}=M_{\eta }[\operatorname {div} (\varepsilon _{\eta }^{2}\nabla \,\eta )-f'(\eta )]\quad {\text{on }}\Omega \times {\mathcal {T}},\quad \eta ={\bar {\eta }}\quad {\text{on }}\partial _{\eta }\Omega \times {\mathcal {T}},}$

${\displaystyle \quad -(\varepsilon _{\eta }^{2}\nabla \,\eta )\cdot m=q\quad {\text{on }}\partial _{q}\Omega \times {\mathcal {T}},\quad \eta =\eta _{o}\quad {\text{on }}\Omega \times \{0\},}$

where ${\displaystyle M_{\eta }}$ is the mobility, ${\displaystyle f}$ is a double-well potential, ${\displaystyle {\bar {\eta }}}$ is the control on the state variable at the portion of the boundary ${\displaystyle \partial _{\eta }\Omega }$, ${\displaystyle q}$ is the source control at ${\displaystyle \partial _{q}\Omega }$, ${\displaystyle \eta _{o}}$ is the initial condition, and ${\displaystyle m}$ is the outward normal to ${\displaystyle \partial \Omega }$.

It is the

• ${\displaystyle \Omega \subset \mathbb {R} ^{n}}$ be an open set,
• ${\displaystyle v_{0}(x)\in L^{2}(\Omega )}$ an arbitrary initial function,
• ${\displaystyle \varepsilon >0}$ and ${\displaystyle T>0}$ two constants.

A function ${\displaystyle v(x,t):\Omega \times [0,T]\to \mathbb {R} }$ is a solution to the Allen–Cahn equation if it solves^[4]

${\displaystyle \partial _{t}v-\Delta _{x}v=-{\frac {1}{\varepsilon ^{2}}}f(v),\quad \Omega \times [0,T]}$

where

• ${\displaystyle \Delta _{x}}$ is the
  Laplacian
  with respect to the space ${\displaystyle x}$,
• ${\displaystyle f(v)=F'(v)}$ is the derivative of a non-negative ${\displaystyle F\in C^{1}(\mathbb {R} )}$ with two minima ${\displaystyle F(\pm 1)=0}$.

Usually, one has the following initial condition with the Neumann boundary condition

${\displaystyle {\begin{cases}v(x,0)=v_{0}(x),&\Omega \times \{0\}\\\partial _{n}v=0,&\partial \Omega \times [0,T]\\\end{cases}}}$

where ${\displaystyle \partial _{n}v}$ is the outer

For ${\displaystyle F(v)}$ one popular candidate is

${\displaystyle F(v)={\frac {(v^{2}-1)^{2}}{4}},\qquad f(v)=v^{3}-v.}$

References

Further reading

• http://www.ctcms.nist.gov/~wcraig/variational/node10.html
• Allen, S. M.; Cahn, J. W. (1975). "Coherent and Incoherent Equilibria in Iron-Rich Iron-Aluminum Alloys". Acta Metall. 23 (9): 1017.
  doi:10.1016/0001-6160(75)90106-6
  .
• Allen, S. M.; Cahn, J. W. (1976). "On Tricritical Points Resulting from the Intersection of Lines of Higher-Order Transitions with Spinodals". Scripta Metallurgica. 10 (5): 451–454.
  doi:10.1016/0036-9748(76)90171-x
  .
• Allen, S. M.; Cahn, J. W. (1976). "Mechanisms of Phase Transformation Within the Miscibility Gap of Fe-Rich Fe-Al Alloys". Acta Metall. 24 (5): 425–437.
  doi:10.1016/0001-6160(76)90063-8
  .
• Cahn, J. W.; Allen, S. M. (1977). "A Microscopic Theory of Domain Wall Motion and Its Experimental Verification in Fe-Al Alloy Domain Growth Kinetics". Journal de Physique. 38: C7–51.
• Allen, S. M.; Cahn, J. W. (1979). "A Microscopic Theory for Antiphase Boundary Motion and Its Application to Antiphase Domain Coarsening". Acta Metall. 27 (6): 1085–1095.
  doi:10.1016/0001-6160(79)90196-2
  .
• S2CID 123291032
  .

External links

• Simulation by Nils Berglund of a solution of the Allen–Cahn equation

This condensed matter physics-related article is a stub. You can help Wikipedia by expanding it.

• v
• t
• e