Catenoid

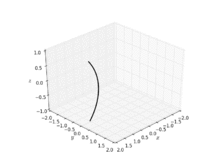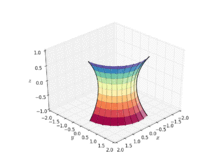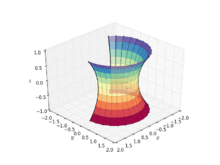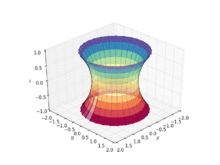
In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis (a surface of revolution).^[1] It is a minimal surface, meaning that it occupies the least area when bounded by a closed space.^[2] It was formally described in 1744 by the mathematician Leonhard Euler.

Soap film attached to twin circular rings will take the shape of a catenoid.^[2] Because they are members of the same associate family of surfaces, a catenoid can be bent into a portion of a helicoid, and vice versa.

Geometry

The catenoid was the first non-trivial minimal

The catenoid may be defined by the following parametric equations:

$${\displaystyle {\begin{aligned}x&=c\cosh {\frac {v}{c}}\cos u\\y&=c\cosh {\frac {v}{c}}\sin u\\z&=v\end{aligned}}}$$

where ${\displaystyle u\in [-\pi ,\pi )}$ and ${\displaystyle v\in \mathbb {R} }$ and ${\displaystyle c}$ is a non-zero real constant.

In cylindrical coordinates:

$${\displaystyle \rho =c\cosh {\frac {z}{c}},}$$

where ${\displaystyle c}$ is a real constant.

A physical model of a catenoid can be formed by dipping two circular rings into a soap solution and slowly drawing the circles apart.

The catenoid may be also defined approximately by the stretched grid method as a facet 3D model.

Helicoid transformation

Because they are members of the same associate family of surfaces, one can bend a catenoid into a portion of a helicoid without stretching. In other words, one can make a (mostly) continuous and isometric deformation of a catenoid to a portion of the helicoid such that every member of the deformation family is minimal (having a mean curvature of zero). A parametrization of such a deformation is given by the system

$${\displaystyle {\begin{aligned}x(u,v)&=\cos \theta \,\sinh v\,\sin u+\sin \theta \,\cosh v\,\cos u\\y(u,v)&=-\cos \theta \,\sinh v\,\cos u+\sin \theta \,\cosh v\,\sin u\\z(u,v)&=u\cos \theta +v\sin \theta \end{aligned}}}$$

${\displaystyle (u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )}$

${\displaystyle -\pi <\theta \leq \pi }$

• ${\displaystyle \theta =\pi }$ corresponds to a right-handed helicoid,
• ${\displaystyle \theta =\pm \pi /2}$ corresponds to a catenoid, and
• ${\displaystyle \theta =0}$ corresponds to a left-handed helicoid.

References