Continuous function

Part of a series of articles about
Calculus
${\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)}$
Fundamental theorem Limits Continuity Rolle's theorem Mean value theorem Inverse function theorem
Differential Definitions Derivative (generalizations) Differential infinitesimal of a function total Concepts Differentiation notation Second derivative Implicit differentiation Logarithmic differentiation Related rates Taylor's theorem Rules and identities Sum Product Chain Power Quotient L'Hôpital's rule Inverse General Leibniz Faà di Bruno's formula Reynolds
Integral Lists of integrals Integral transform Leibniz integral rule Definitions Antiderivative Integral (improper) Riemann integral Lebesgue integration Contour integration Integral of inverse functions Integration by Parts Discs Cylindrical shells Substitution (trigonometric, tangent half-angle, Euler) Euler's formula Partial fractions (Heaviside's method ) Changing order Reduction formulae Differentiating under the integral sign Risch algorithm
Series arithmetico-geometric ) Harmonic Alternating Power Binomial Taylor Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel
Vector Gradient Divergence Curl Laplacian Directional derivative Identities Theorems Gradient Green's Stokes' Divergence generalized Stokes Helmholtz decomposition
Multivariable Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian Hessian
Advanced Calculus on Euclidean space Generalized functions Limit of distributions
Specialized Fractional Malliavin Stochastic Variations
Miscellanea Precalculus History Glossary List of topics Integration Bee Mathematical analysis Nonstandard analysis
v t e

In

was introduced to formalize the definition of continuity.

Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their definition is the basis of topology.

A stronger form of continuity is uniform continuity. In order theory, especially in domain theory, a related concept of continuity is Scott continuity.

As an example, the function H(t) denoting the height of a growing flower at time t would be considered continuous. In contrast, the function M(t) denoting the amount of money in a bank account at time t would be considered discontinuous since it "jumps" at each point in time when money is deposited or withdrawn.

A form of the epsilon–delta definition of continuity was first given by Bernard Bolzano in 1817. Augustin-Louis Cauchy defined continuity of ${\displaystyle y=f(x)}$ as follows: an infinitely small increment ${\displaystyle \alpha }$ of the independent variable x always produces an infinitely small change ${\displaystyle f(x+\alpha )-f(x)}$ of the dependent variable y (see e.g.

Real functions

Definition

A

Continuity of real functions is usually defined in terms of limits. A function f with variable x is continuous at the real number c, if the limit of ${\displaystyle f(x),}$ as x tends to c, is equal to ${\displaystyle f(c).}$

There are several different definitions of the (global) continuity of a function, which depend on the nature of its domain.

A function is continuous on an

if the interval is contained in the function's domain and the function is continuous at every interval point. A function that is continuous on the interval ${\displaystyle (-\infty ,+\infty )}$ (the whole are continuous everywhere.

A function is continuous on a

interval; if the interval is contained in the domain of the function, the function is continuous at every interior point of the interval, and the value of the function at each endpoint that belongs to the interval is the limit of the values of the function when the variable tends to the endpoint from the interior of the interval. For example, the function ${\displaystyle f(x)={\sqrt {x}}}$ is continuous on its whole domain, which is the closed interval ${\displaystyle [0,+\infty ).}$

Many commonly encountered functions are

${\textstyle x\mapsto {\frac {1}{x}}}$ and the ${\displaystyle x\mapsto \tan x.}$ When they are continuous on their domain, one says, in some contexts, that they are continuous, although they are not continuous everywhere. In other contexts, mainly when one is interested in their behavior near the exceptional points, one says they are discontinuous.

A partial function is discontinuous at a point if the point belongs to the

of its domain, and either the point does not belong to the domain of the function or the function is not continuous at the point. For example, the functions ${\textstyle x\mapsto {\frac {1}{x}}}$ and ${\textstyle x\mapsto \sin({\frac {1}{x}})}$ are discontinuous at 0, and remain discontinuous whichever value is chosen for defining them at 0. A point where a function is discontinuous is called a discontinuity.

Using mathematical notation, several ways exist to define continuous functions in the three senses mentioned above.

Let $${\displaystyle f:D\to \mathbb {R} }$$ be a function defined on a subset ${\displaystyle D}$ of the set ${\displaystyle \mathbb {R} }$ of real numbers.

This subset ${\displaystyle D}$ is the domain of f. Some possible choices include

• ${\displaystyle D=\mathbb {R} }$: i.e., ${\displaystyle D}$ is the whole set of real numbers. or, for a and b real numbers,
• ${\displaystyle D=[a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}}$: ${\displaystyle D}$ is a
  closed interval
  , or
• ${\displaystyle D=(a,b)=\{x\in \mathbb {R} \mid a<x<b\}}$: ${\displaystyle D}$ is an
  open interval
  .

In the case of the domain ${\displaystyle D}$ being defined as an open interval, ${\displaystyle a}$ and ${\displaystyle b}$ do not belong to ${\displaystyle D}$, and the values of ${\displaystyle f(a)}$ and ${\displaystyle f(b)}$ do not matter for continuity on ${\displaystyle D}$.

The function f is continuous at some point c of its domain if the limit of ${\displaystyle f(x),}$ as x approaches c through the domain of f, exists and is equal to ${\displaystyle f(c).}$^[9] In mathematical notation, this is written as $${\displaystyle \lim _{x\to c}{f(x)}=f(c).}$$ In detail this means three conditions: first, f has to be defined at c (guaranteed by the requirement that c is in the domain of f). Second, the limit of that equation has to exist. Third, the value of this limit must equal ${\displaystyle f(c).}$

(Here, we have assumed that the domain of f does not have any isolated points.)

A

of a point c is a set that contains, at least, all points within some fixed distance of c. Intuitively, a function is continuous at a point c if the range of f over the neighborhood of c shrinks to a single point ${\displaystyle f(c)}$ as the width of the neighborhood around c shrinks to zero. More precisely, a function f is continuous at a point c of its domain if, for any neighborhood ${\displaystyle N_{1}(f(c))}$ there is a neighborhood ${\displaystyle N_{2}(c)}$ in its domain such that ${\displaystyle f(x)\in N_{1}(f(c))}$ whenever ${\displaystyle x\in N_{2}(c).}$

As neighborhoods are defined in any topological space, this definition of a continuous function applies not only for real functions but also when the domain and the codomain are topological spaces and is thus the most general definition. It follows that a function is automatically continuous at every isolated point of its domain. For example, every real-valued function on the integers is continuous.

One can instead require that for any

${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ of points in the domain which to c, the corresponding sequence ${\displaystyle \left(f(x_{n})\right)_{n\in \mathbb {N} }}$ converges to ${\displaystyle f(c).}$ In mathematical notation, $${\displaystyle \forall (x_{n})_{n\in \mathbb {N} }\subset D:\lim _{n\to \infty }x_{n}=c\Rightarrow \lim _{n\to \infty }f(x_{n})=f(c)\,.}$$

Explicitly including the definition of the limit of a function, we obtain a self-contained definition: Given a function ${\displaystyle f:D\to \mathbb {R} }$ as above and an element ${\displaystyle x_{0}}$ of the domain ${\displaystyle D}$, ${\displaystyle f}$ is said to be continuous at the point ${\displaystyle x_{0}}$ when the following holds: For any positive real number ${\displaystyle \varepsilon >0,}$ however small, there exists some positive real number ${\displaystyle \delta >0}$ such that for all ${\displaystyle x}$ in the domain of ${\displaystyle f}$ with ${\displaystyle x_{0}-\delta <x<x_{0}+\delta ,}$ the value of ${\displaystyle f(x)}$ satisfies $${\displaystyle f\left(x_{0}\right)-\varepsilon <f(x)<f(x_{0})+\varepsilon .}$$

Alternatively written, continuity of ${\displaystyle f:D\to \mathbb {R} }$ at ${\displaystyle x_{0}\in D}$ means that for every ${\displaystyle \varepsilon >0,}$ there exists a ${\displaystyle \delta >0}$ such that for all ${\displaystyle x\in D}$: $${\displaystyle \left|x-x_{0}\right|<\delta ~~{\text{ implies }}~~|f(x)-f(x_{0})|<\varepsilon .}$$

More intuitively, we can say that if we want to get all the ${\displaystyle f(x)}$ values to stay in some small

around ${\displaystyle f\left(x_{0}\right),}$ we need to choose a small enough neighborhood for the ${\displaystyle x}$ values around ${\displaystyle x_{0}.}$ If we can do that no matter how small the ${\displaystyle f(x_{0})}$ neighborhood is, then ${\displaystyle f}$ is continuous at ${\displaystyle x_{0}.}$

In modern terms, this is generalized by the definition of continuity of a function with respect to a

.

Weierstrass had required that the interval ${\displaystyle x_{0}-\delta <x<x_{0}+\delta }$ be entirely within the domain ${\displaystyle D}$, but Jordan removed that restriction.

In proofs and numerical analysis, we often need to know how fast limits are converging, or in other words, control of the remainder. We can formalize this to a definition of continuity. A function ${\displaystyle C:[0,\infty )\to [0,\infty ]}$ is called a control function if

• C is non-decreasing
• ${\displaystyle \inf _{\delta >0}C(\delta )=0}$

A function ${\displaystyle f:D\to R}$ is C-continuous at ${\displaystyle x_{0}}$ if there exists such a neighbourhood ${\textstyle N(x_{0})}$ that $${\displaystyle |f(x)-f(x_{0})|\leq C\left(\left|x-x_{0}\right|\right){\text{ for all }}x\in D\cap N(x_{0})}$$

A function is continuous in ${\displaystyle x_{0}}$ if it is C-continuous for some control function C.

This approach leads naturally to refining the notion of continuity by restricting the set of admissible control functions. For a given set of control functions ${\displaystyle {\mathcal {C}}}$ a function is ${\displaystyle {\mathcal {C}}}$-continuous if it is ${\displaystyle C}$-continuous for some ${\displaystyle C\in {\mathcal {C}}.}$ For example, the

below are defined by the set of control functions $${\displaystyle {\mathcal {C}}_{\mathrm {Lipschitz} }=\{C:C(\delta )=K|\delta |,\ K>0\}}$$ $${\displaystyle {\mathcal {C}}_{{\text{Hölder}}-\alpha }=\{C:C(\delta )=K|\delta |^{\alpha },\ K>0\}}$$ $${\displaystyle {\mathcal {C}}_{\text{uniform cont.}}=\{C:C(0)=0\}}$$ respectively.

Continuity can also be defined in terms of oscillation: a function f is continuous at a point ${\displaystyle x_{0}}$ if and only if its oscillation at that point is zero;^[10] in symbols, ${\displaystyle \omega _{f}(x_{0})=0.}$ A benefit of this definition is that it quantifies discontinuity: the oscillation gives how much the function is discontinuous at a point.

This definition is helpful in descriptive set theory to study the set of discontinuities and continuous points – the continuous points are the intersection of the sets where the oscillation is less than ${\displaystyle \varepsilon }$ (hence a ${\displaystyle G_{\delta }}$ set) – and gives a rapid proof of one direction of the

The oscillation is equivalent to the ${\displaystyle \varepsilon -\delta }$ definition by a simple re-arrangement and by using a limit (

lim inf

) to define oscillation: if (at a given point) for a given ${\displaystyle \varepsilon _{0}}$ there is no ${\displaystyle \delta }$ that satisfies the ${\displaystyle \varepsilon -\delta }$ definition, then the oscillation is at least ${\displaystyle \varepsilon _{0},}$ and conversely if for every ${\displaystyle \varepsilon }$ there is a desired ${\displaystyle \delta ,}$ the oscillation is 0. The oscillation definition can be naturally generalized to maps from a topological space to a metric space.

. In nonstandard analysis, continuity can be defined as follows.

(see microcontinuity). In other words, an infinitesimal increment of the independent variable always produces an infinitesimal change of the dependent variable, giving a modern expression to Augustin-Louis Cauchy's definition of continuity.

Checking the continuity of a given function can be simplified by checking one of the above defining properties for the building blocks of the given function. It is straightforward to show that the sum of two functions, continuous on some domain, is also continuous on this domain. Given $${\displaystyle f,g\colon D\to \mathbb {R} ,}$$ then the sum of continuous functions $${\displaystyle s=f+g}$$ (defined by ${\displaystyle s(x)=f(x)+g(x)}$ for all ${\displaystyle x\in D}$) is continuous in ${\displaystyle D.}$

The same holds for the product of continuous functions, $${\displaystyle p=f\cdot g}$$ (defined by ${\displaystyle p(x)=f(x)\cdot g(x)}$ for all ${\displaystyle x\in D}$) is continuous in ${\displaystyle D.}$

Combining the above preservations of continuity and the continuity of constant functions and of the identity function ${\displaystyle I(x)=x}$ on ${\displaystyle \mathbb {R} }$, one arrives at the continuity of all polynomial functions on ${\displaystyle \mathbb {R} }$, such as $${\displaystyle f(x)=x^{3}+x^{2}-5x+3}$$ (pictured on the right).

In the same way, it can be shown that the reciprocal of a continuous function $${\displaystyle r=1/f}$$ (defined by ${\displaystyle r(x)=1/f(x)}$ for all ${\displaystyle x\in D}$ such that ${\displaystyle f(x)\neq 0}$) is continuous in ${\displaystyle D\setminus \{x:f(x)=0\}.}$

This implies that, excluding the roots of ${\displaystyle g,}$ the quotient of continuous functions $${\displaystyle q=f/g}$$ (defined by ${\displaystyle q(x)=f(x)/g(x)}$ for all ${\displaystyle x\in D}$, such that ${\displaystyle g(x)\neq 0}$) is also continuous on ${\displaystyle D\setminus \{x:g(x)=0\}}$.

For example, the function (pictured) $${\displaystyle y(x)={\frac {2x-1}{x+2}}}$$ is defined for all real numbers ${\displaystyle x\neq -2}$ and is continuous at every such point. Thus, it is a continuous function. The question of continuity at ${\displaystyle x=-2}$ does not arise since ${\displaystyle x=-2}$ is not in the domain of ${\displaystyle y.}$ There is no continuous function ${\displaystyle F:\mathbb {R} \to \mathbb {R} }$ that agrees with ${\displaystyle y(x)}$ for all ${\displaystyle x\neq -2.}$

Since the function

${\displaystyle G(x)=\sin(x)/x,}$ is defined and continuous for all real ${\displaystyle x\neq 0.}$ However, unlike the previous example, G can be extended to a continuous function on all real numbers, by defining the value ${\displaystyle G(0)}$ to be 1, which is the limit of ${\displaystyle G(x),}$ when x approaches 0, i.e., $${\displaystyle G(0)=\lim _{x\to 0}{\frac {\sin x}{x}}=1.}$$

Thus, by setting

${\displaystyle G(x)={\begin{cases}{\frac {\sin(x)}{x}}&{\text{ if }}x\neq 0\\1&{\text{ if }}x=0,\end{cases}}}$

the sinc-function becomes a continuous function on all real numbers. The term removable singularity is used in such cases when (re)defining values of a function to coincide with the appropriate limits make a function continuous at specific points.

A more involved construction of continuous functions is the function composition. Given two continuous functions $${\displaystyle g:D_{g}\subseteq \mathbb {R} \to R_{g}\subseteq \mathbb {R} \quad {\text{ and }}\quad f:D_{f}\subseteq \mathbb {R} \to R_{f}\subseteq D_{g},}$$ their composition, denoted as ${\displaystyle c=g\circ f:D_{f}\to \mathbb {R} ,}$ and defined by ${\displaystyle c(x)=g(f(x)),}$ is continuous.

This construction allows stating, for example, that $${\displaystyle e^{\sin(\ln x)}}$$ is continuous for all ${\displaystyle x>0.}$

An example of a discontinuous function is the Heaviside step function ${\displaystyle H}$, defined by $${\displaystyle H(x)={\begin{cases}1&{\text{ if }}x\geq 0\\0&{\text{ if }}x<0\end{cases}}}$$

Pick for instance ${\displaystyle \varepsilon =1/2}$. Then there is no ${\displaystyle \delta }$-neighborhood around ${\displaystyle x=0}$, i.e. no open interval ${\displaystyle (-\delta ,\;\delta )}$ with ${\displaystyle \delta >0,}$ that will force all the ${\displaystyle H(x)}$ values to be within the ${\displaystyle \varepsilon }$-neighborhood of ${\displaystyle H(0)}$, i.e. within ${\displaystyle (1/2,\;3/2)}$. Intuitively, we can think of this type of discontinuity as a sudden

in function values.

Similarly, the signum or sign function $${\displaystyle \operatorname {sgn}(x)={\begin{cases}\;\;\ 1&{\text{ if }}x>0\\\;\;\ 0&{\text{ if }}x=0\\-1&{\text{ if }}x<0\end{cases}}}$$ is discontinuous at ${\displaystyle x=0}$ but continuous everywhere else. Yet another example: the function $${\displaystyle f(x)={\begin{cases}\sin \left(x^{-2}\right)&{\text{ if }}x\neq 0\\0&{\text{ if }}x=0\end{cases}}}$$ is continuous everywhere apart from ${\displaystyle x=0}$.

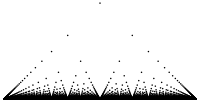
Besides plausible continuities and discontinuities like above, there are also functions with a behavior, often coined pathological, for example, Thomae's function, $${\displaystyle f(x)={\begin{cases}1&{\text{ if }}x=0\\{\frac {1}{q}}&{\text{ if }}x={\frac {p}{q}}{\text{(in lowest terms) is a rational number}}\\0&{\text{ if }}x{\text{ is irrational}}.\end{cases}}}$$ is continuous at all irrational numbers and discontinuous at all rational numbers. In a similar vein,

for the set of rational numbers, $${\displaystyle D(x)={\begin{cases}0&{\text{ if }}x{\text{ is irrational }}(\in \mathbb {R} \setminus \mathbb {Q} )\\1&{\text{ if }}x{\text{ is rational }}(\in \mathbb {Q} )\end{cases}}}$$ is nowhere continuous.

Properties

A useful lemma

Let ${\displaystyle f(x)}$ be a function that is continuous at a point ${\displaystyle x_{0},}$ and ${\displaystyle y_{0}}$ be a value such ${\displaystyle f\left(x_{0}\right)\neq y_{0}.}$ Then ${\displaystyle f(x)\neq y_{0}}$ throughout some neighbourhood of ${\displaystyle x_{0}.}$[13]

Proof: By the definition of continuity, take ${\displaystyle \varepsilon ={\frac {|y_{0}-f(x_{0})|}{2}}>0}$ , then there exists ${\displaystyle \delta >0}$ such that $${\displaystyle \left|f(x)-f(x_{0})\right|<{\frac {\left|y_{0}-f(x_{0})\right|}{2}}\quad {\text{ whenever }}\quad |x-x_{0}|<\delta }$$ Suppose there is a point in the neighbourhood ${\displaystyle |x-x_{0}|<\delta }$ for which ${\displaystyle f(x)=y_{0};}$ then we have the contradiction $${\displaystyle \left|f(x_{0})-y_{0}\right|<{\frac {\left|f(x_{0})-y_{0}\right|}{2}}.}$$

The intermediate value theorem is an existence theorem, based on the real number property of completeness, and states:

If the real-valued function f is continuous on the closed interval ${\displaystyle [a,b],}$ and k is some number between ${\displaystyle f(a)}$ and ${\displaystyle f(b),}$ then there is some number ${\displaystyle c\in [a,b],}$ such that ${\displaystyle f(c)=k.}$

For example, if a child grows from 1 m to 1.5 m between the ages of two and six years, then, at some time between two and six years of age, the child's height must have been 1.25 m.

As a consequence, if f is continuous on ${\displaystyle [a,b]}$ and ${\displaystyle f(a)}$ and ${\displaystyle f(b)}$ differ in sign, then, at some point ${\displaystyle c\in [a,b],}$ ${\displaystyle f(c)}$ must equal

.

The extreme value theorem states that if a function f is defined on a closed interval ${\displaystyle [a,b]}$ (or any closed and bounded set) and is continuous there, then the function attains its maximum, i.e. there exists ${\displaystyle c\in [a,b]}$ with ${\displaystyle f(c)\geq f(x)}$ for all ${\displaystyle x\in [a,b].}$ The same is true of the minimum of f. These statements are not, in general, true if the function is defined on an open interval ${\displaystyle (a,b)}$ (or any set that is not both closed and bounded), as, for example, the continuous function ${\displaystyle f(x)={\frac {1}{x}},}$ defined on the open interval (0,1), does not attain a maximum, being unbounded above.

Every differentiable function $${\displaystyle f:(a,b)\to \mathbb {R} }$$ is continuous, as can be shown. The converse does not hold: for example, the absolute value function

${\displaystyle f(x)=|x|={\begin{cases}\;\;\ x&{\text{ if }}x\geq 0\\-x&{\text{ if }}x<0\end{cases}}}$

is everywhere continuous. However, it is not differentiable at ${\displaystyle x=0}$ (but is so everywhere else). Weierstrass's function is also everywhere continuous but nowhere differentiable.

The derivative f′(x) of a differentiable function f(x) need not be continuous. If f′(x) is continuous, f(x) is said to be continuously differentiable. The set of such functions is denoted ${\displaystyle C^{1}((a,b)).}$ More generally, the set of functions $${\displaystyle f:\Omega \to \mathbb {R} }$$ (from an open interval (or

of ${\displaystyle \mathbb {R} }$) ${\displaystyle \Omega }$ to the reals) such that f is ${\displaystyle n}$ times differentiable and such that the ${\displaystyle n}$-th derivative of f is continuous is denoted ${\displaystyle C^{n}(\Omega ).}$ See . In the field of computer graphics, properties related (but not identical) to ${\displaystyle C^{0},C^{1},C^{2}}$ are sometimes called ${\displaystyle G^{0}}$ (continuity of position), ${\displaystyle G^{1}}$ (continuity of tangency), and ${\displaystyle G^{2}}$ (continuity of curvature); see Smoothness of curves and surfaces.

Every continuous function $${\displaystyle f:[a,b]\to \mathbb {R} }$$ is

shows.

Pointwise and uniform limits

Given a

$${\displaystyle f_{1},f_{2},\dotsc :I\to \mathbb {R} }$$ of functions such that the limit $${\displaystyle f(x):=\lim _{n\to \infty }f_{n}(x)}$$ exists for all ${\displaystyle x\in D,}$, the resulting function ${\displaystyle f(x)}$ is referred to as the pointwise limit of the sequence of functions ${\displaystyle \left(f_{n}\right)_{n\in N}.}$ The pointwise limit function need not be continuous, even if all functions ${\displaystyle f_{n}}$ are continuous, as the animation at the right shows. However, f is continuous if all functions ${\displaystyle f_{n}}$ are continuous and the sequence are continuous.

Discontinuous functions may be discontinuous in a restricted way, giving rise to the concept of directional continuity (or right and left continuous functions) and semi-continuity. Roughly speaking, a function is right-continuous if no jump occurs when the limit point is approached from the right. Formally, f is said to be right-continuous at the point c if the following holds: For any number ${\displaystyle \varepsilon >0}$ however small, there exists some number ${\displaystyle \delta >0}$ such that for all x in the domain with ${\displaystyle c<x<c+\delta ,}$ the value of ${\displaystyle f(x)}$ will satisfy $${\displaystyle |f(x)-f(c)|<\varepsilon .}$$

This is the same condition as continuous functions, except it is required to hold for x strictly larger than c only. Requiring it instead for all x with ${\displaystyle c-\delta <x<c}$ yields the notion of left-continuous functions. A function is continuous if and only if it is both right-continuous and left-continuous.

A function f is lower semi-continuous if, roughly, any jumps that might occur only go down, but not up. That is, for any ${\displaystyle \varepsilon >0,}$ there exists some number ${\displaystyle \delta >0}$ such that for all x in the domain with ${\displaystyle |x-c|<\delta ,}$ the value of ${\displaystyle f(x)}$ satisfies $${\displaystyle f(x)\geq f(c)-\epsilon .}$$ The reverse condition is upper semi-continuity.

The concept of continuous real-valued functions can be generalized to functions between metric spaces. A metric space is a set ${\displaystyle X}$ equipped with a function (called

) ${\displaystyle d_{X},}$ that can be thought of as a measurement of the distance of any two elements in X. Formally, the metric is a function $${\displaystyle d_{X}:X\times X\to \mathbb {R} }$$ that satisfies a number of requirements, notably the triangle inequality. Given two metric spaces ${\displaystyle \left(X,d_{X}\right)}$ and ${\displaystyle \left(Y,d_{Y}\right)}$ and a function $${\displaystyle f:X\to Y}$$ then ${\displaystyle f}$ is continuous at the point ${\displaystyle c\in X}$ (with respect to the given metrics) if for any positive real number ${\displaystyle \varepsilon >0,}$ there exists a positive real number ${\displaystyle \delta >0}$ such that all ${\displaystyle x\in X}$ satisfying ${\displaystyle d_{X}(x,c)<\delta }$ will also satisfy ${\displaystyle d_{Y}(f(x),f(c))<\varepsilon .}$ As in the case of real functions above, this is equivalent to the condition that for every sequence ${\displaystyle \left(x_{n}\right)}$ in ${\displaystyle X}$ with limit ${\displaystyle \lim x_{n}=c,}$ we have ${\displaystyle \lim f\left(x_{n}\right)=f(c).}$ The latter condition can be weakened as follows: ${\displaystyle f}$ is continuous at the point ${\displaystyle c}$ if and only if for every convergent sequence ${\displaystyle \left(x_{n}\right)}$ in ${\displaystyle X}$ with limit ${\displaystyle c}$, the sequence ${\displaystyle \left(f\left(x_{n}\right)\right)}$ is a Cauchy sequence, and ${\displaystyle c}$ is in the domain of ${\displaystyle f}$.

The set of points at which a function between metric spaces is continuous is a ${\displaystyle G_{\delta }}$ set – this follows from the ${\displaystyle \varepsilon -\delta }$ definition of continuity.

This notion of continuity is applied, for example, in

$${\displaystyle T:V\to W}$$ between normed vector spaces ${\displaystyle V}$ and ${\displaystyle W}$ (which are vector spaces equipped with a compatible norm, denoted ${\displaystyle \|x\|}$) is continuous if and only if it is , that is, there is a constant ${\displaystyle K}$ such that $${\displaystyle \|T(x)\|\leq K\|x\|}$$ for all ${\displaystyle x\in V.}$

The concept of continuity for functions between metric spaces can be strengthened in various ways by limiting the way ${\displaystyle \delta }$ depends on ${\displaystyle \varepsilon }$ and c in the definition above. Intuitively, a function f as above is

if the ${\displaystyle \delta }$ does not depend on the point c. More precisely, it is required that for every real number ${\displaystyle \varepsilon >0}$ there exists ${\displaystyle \delta >0}$ such that for every ${\displaystyle c,b\in X}$ with ${\displaystyle d_{X}(b,c)<\delta ,}$ we have that ${\displaystyle d_{Y}(f(b),f(c))<\varepsilon .}$ Thus, any uniformly continuous function is continuous. The converse does not generally hold but holds when the domain space X is

A function is

Hölder continuous

with exponent α (a real number) if there is a constant K such that for all ${\displaystyle b,c\in X,}$ the inequality $${\displaystyle d_{Y}(f(b),f(c))\leq K\cdot (d_{X}(b,c))^{\alpha }}$$ holds. Any Hölder continuous function is uniformly continuous. The particular case ${\displaystyle \alpha =1}$ is referred to as Lipschitz continuity. That is, a function is Lipschitz continuous if there is a constant K such that the inequality $${\displaystyle d_{Y}(f(b),f(c))\leq K\cdot d_{X}(b,c)}$$ holds for any ${\displaystyle b,c\in X.}$^[15] The Lipschitz condition occurs, for example, in the Picard–Lindelöf theorem concerning the solutions of ordinary differential equations.

Another, more abstract, notion of continuity is the continuity of functions between

of X (with respect to the topology).

A function $${\displaystyle f:X\to Y}$$ between two topological spaces X and Y is continuous if for every open set ${\displaystyle V\subseteq Y,}$ the inverse image $${\displaystyle f^{-1}(V)=\{x\in X\;|\;f(x)\in V\}}$$ is an open subset of X. That is, f is a function between the sets X and Y (not on the elements of the topology ${\displaystyle T_{X}}$), but the continuity of f depends on the topologies used on X and Y.

This is equivalent to the condition that the preimages of the closed sets (which are the complements of the open subsets) in Y are closed in X.

An extreme example: if a set X is given the

(in which every subset is open), all functions $${\displaystyle f:X\to T}$$ to any topological space T are continuous. On the other hand, if X is equipped with the , then the only continuous functions are the constant functions. Conversely, any function whose codomain is indiscrete is continuous.

The translation in the language of neighborhoods of the ${\displaystyle (\varepsilon ,\delta )}$-definition of continuity leads to the following definition of the continuity at a point:

A function ${\displaystyle f:X\to Y}$ is continuous at a point ${\displaystyle x\in X}$ if and only if for any neighborhood V of ${\displaystyle f(x)}$ in Y, there is a neighborhood U of ${\displaystyle x}$ such that ${\displaystyle f(U)\subseteq V.}$

This definition is equivalent to the same statement with neighborhoods restricted to open neighborhoods and can be restated in several ways by using

rather than images.

Also, as every set that contains a neighborhood is also a neighborhood, and ${\displaystyle f^{-1}(V)}$ is the largest subset U of X such that ${\displaystyle f(U)\subseteq V,}$ this definition may be simplified into:

A function ${\displaystyle f:X\to Y}$ is continuous at a point ${\displaystyle x\in X}$ if and only if ${\displaystyle f^{-1}(V)}$ is a neighborhood of ${\displaystyle x}$ for every neighborhood V of ${\displaystyle f(x)}$ in Y.

As an open set is a set that is a neighborhood of all its points, a function ${\displaystyle f:X\to Y}$ is continuous at every point of X if and only if it is a continuous function.

If X and Y are metric spaces, it is equivalent to consider the

centered at x and f(x) instead of all neighborhoods. This gives back the above ${\displaystyle \varepsilon -\delta }$ definition of continuity in the context of metric spaces. In general topological spaces, there is no notion of nearness or distance. If, however, the target space is a Hausdorff space, it is still true that f is continuous at a if and only if the limit of f as x approaches a is f(a). At an isolated point, every function is continuous.

Given ${\displaystyle x\in X,}$ a map ${\displaystyle f:X\to Y}$ is continuous at ${\displaystyle x}$ if and only if whenever ${\displaystyle {\mathcal {B}}}$ is a filter on ${\displaystyle X}$ that

to ${\displaystyle x}$ in ${\displaystyle X,}$ which is expressed by writing ${\displaystyle {\mathcal {B}}\to x,}$ then necessarily ${\displaystyle f({\mathcal {B}})\to f(x)}$ in ${\displaystyle Y.}$ If ${\displaystyle {\mathcal {N}}(x)}$ denotes the at ${\displaystyle x}$ then ${\displaystyle f:X\to Y}$ is continuous at ${\displaystyle x}$ if and only if ${\displaystyle f({\mathcal {N}}(x))\to f(x)}$ in ${\displaystyle Y.}$

prefilter

${\displaystyle f({\mathcal {N}}(x))}$ is a

filter base

for the neighborhood filter of ${\displaystyle f(x)}$ in ${\displaystyle Y.}$^[16]

Alternative definitions

Several

equivalent definitions for a topological structure

exist; thus, several equivalent ways exist to define a continuous function.

Sequences and nets

In several contexts, the topology of a space is conveniently specified in terms of

limit points. This is often accomplished by specifying when a point is the limit of a sequence. Still, for some spaces that are too large in some sense, one specifies also when a point is the limit of more general sets of points indexed by a directed set, known as nets

. A function is (Heine-)continuous only if it takes limits of sequences to limits of sequences. In the former case, preservation of limits is also sufficient; in the latter, a function may preserve all limits of sequences yet still fail to be continuous, and preservation of nets is a necessary and sufficient condition.

In detail, a function ${\displaystyle f:X\to Y}$ is

sequentially continuous

if whenever a sequence ${\displaystyle \left(x_{n}\right)}$ in ${\displaystyle X}$ converges to a limit ${\displaystyle x,}$ the sequence ${\displaystyle \left(f\left(x_{n}\right)\right)}$ converges to ${\displaystyle f(x).}$ Thus, sequentially continuous functions "preserve sequential limits." Every continuous function is sequentially continuous. If ${\displaystyle X}$ is a first-countable space and countable choice holds, then the converse also holds: any function preserving sequential limits is continuous. In particular, if ${\displaystyle X}$ is a metric space, sequential continuity and continuity are equivalent. For non-first-countable spaces, sequential continuity might be strictly weaker than continuity. (The spaces for which the two properties are equivalent are called sequential spaces.) This motivates the consideration of nets instead of sequences in general topological spaces. Continuous functions preserve the limits of nets, and this property characterizes continuous functions.

For instance, consider the case of real-valued functions of one real variable:^[17]

Theorem—A function ${\displaystyle f:A\subseteq \mathbb {R} \to \mathbb {R} }$ is continuous at ${\displaystyle x_{0}}$ if and only if it is

sequentially continuous

at that point.

Proof

Proof. Assume that ${\displaystyle f:A\subseteq \mathbb {R} \to \mathbb {R} }$ is continuous at ${\displaystyle x_{0}}$ (in the sense of ${\displaystyle \epsilon -\delta }$ continuity). Let ${\displaystyle \left(x_{n}\right)_{n\geq 1}}$ be a sequence converging at ${\displaystyle x_{0}}$ (such a sequence always exists, for example, ${\displaystyle x_{n}=x,{\text{ for all }}n}$); since ${\displaystyle f}$ is continuous at ${\displaystyle x_{0}}$ $${\displaystyle \forall \epsilon >0\,\exists \delta _{\epsilon }>0:0<|x-x_{0}|<\delta _{\epsilon }\implies |f(x)-f(x_{0})|<\epsilon .\quad (*)}$$ For any such ${\displaystyle \delta _{\epsilon }}$ we can find a natural number ${\displaystyle \nu _{\epsilon }>0}$ such that for all ${\displaystyle n>\nu _{\epsilon },}$ $${\displaystyle |x_{n}-x_{0}|<\delta _{\epsilon },}$$ since ${\displaystyle \left(x_{n}\right)}$ converges at ${\displaystyle x_{0}}$; combining this with ${\displaystyle (*)}$ we obtain $${\displaystyle \forall \epsilon >0\,\exists \nu _{\epsilon }>0:\forall n>\nu _{\epsilon }\quad |f(x_{n})-f(x_{0})|<\epsilon .}$$ Assume on the contrary that ${\displaystyle f}$ is sequentially continuous and proceed by contradiction: suppose ${\displaystyle f}$ is not continuous at ${\displaystyle x_{0}}$ $${\displaystyle \exists \epsilon >0:\forall \delta _{\epsilon }>0,\,\exists x_{\delta _{\epsilon }}:0<|x_{\delta _{\epsilon }}-x_{0}|<\delta _{\epsilon }\implies |f(x_{\delta _{\epsilon }})-f(x_{0})|>\epsilon }$$ then we can take ${\displaystyle \delta _{\epsilon }=1/n,\,\forall n>0}$ and call the corresponding point ${\displaystyle x_{\delta _{\epsilon }}=:x_{n}}$: in this way we have defined a sequence ${\displaystyle (x_{n})_{n\geq 1}}$ such that $${\displaystyle \forall n>0\quad |x_{n}-x_{0}|<{\frac {1}{n}},\quad |f(x_{n})-f(x_{0})|>\epsilon }$$ by construction ${\displaystyle x_{n}\to x_{0}}$ but ${\displaystyle f(x_{n})\not \to f(x_{0})}$, which contradicts the hypothesis of sequential continuity. ${\displaystyle \blacksquare }$

Closure operator and interior operator definitions

In terms of the interior operator, a function ${\displaystyle f:X\to Y}$ between topological spaces is continuous if and only if for every subset ${\displaystyle B\subseteq Y,}$ $${\displaystyle f^{-1}\left(\operatorname {int} _{Y}B\right)~\subseteq ~\operatorname {int} _{X}\left(f^{-1}(B)\right).}$$

In terms of the closure operator, ${\displaystyle f:X\to Y}$ is continuous if and only if for every subset ${\displaystyle A\subseteq X,}$ $${\displaystyle f\left(\operatorname {cl} _{X}A\right)~\subseteq ~\operatorname {cl} _{Y}(f(A)).}$$ That is to say, given any element ${\displaystyle x\in X}$ that belongs to the closure of a subset ${\displaystyle A\subseteq X,}$ ${\displaystyle f(x)}$ necessarily belongs to the closure of ${\displaystyle f(A)}$ in ${\displaystyle Y.}$ If we declare that a point ${\displaystyle x}$ is close to a subset ${\displaystyle A\subseteq X}$ if ${\displaystyle x\in \operatorname {cl} _{X}A,}$ then this terminology allows for a plain English description of continuity: ${\displaystyle f}$ is continuous if and only if for every subset ${\displaystyle A\subseteq X,}$ ${\displaystyle f}$ maps points that are close to ${\displaystyle A}$ to points that are close to ${\displaystyle f(A).}$ Similarly, ${\displaystyle f}$ is continuous at a fixed given point ${\displaystyle x\in X}$ if and only if whenever ${\displaystyle x}$ is close to a subset ${\displaystyle A\subseteq X,}$ then ${\displaystyle f(x)}$ is close to ${\displaystyle f(A).}$

Instead of specifying topological spaces by their open subsets, any topology on ${\displaystyle X}$ can

interior operator

. Specifically, the map that sends a subset ${\displaystyle A}$ of a topological space ${\displaystyle X}$ to its topological closure ${\displaystyle \operatorname {cl} _{X}A}$ satisfies the

closure operator

${\displaystyle A\mapsto \operatorname {cl} A}$ there exists a unique topology ${\displaystyle \tau }$ on ${\displaystyle X}$ (specifically, ${\displaystyle \tau :=\{X\setminus \operatorname {cl} A:A\subseteq X\}}$) such that for every subset ${\displaystyle A\subseteq X,}$ ${\displaystyle \operatorname {cl} A}$ is equal to the topological closure ${\displaystyle \operatorname {cl} _{(X,\tau )}A}$ of ${\displaystyle A}$ in ${\displaystyle (X,\tau ).}$ If the sets ${\displaystyle X}$ and ${\displaystyle Y}$ are each associated with closure operators (both denoted by ${\displaystyle \operatorname {cl} }$) then a map ${\displaystyle f:X\to Y}$ is continuous if and only if ${\displaystyle f(\operatorname {cl} A)\subseteq \operatorname {cl} (f(A))}$ for every subset ${\displaystyle A\subseteq X.}$

Similarly, the map that sends a subset ${\displaystyle A}$ of ${\displaystyle X}$ to its topological interior ${\displaystyle \operatorname {int} _{X}A}$ defines an

interior operator

. Conversely, any interior operator ${\displaystyle A\mapsto \operatorname {int} A}$ induces a unique topology ${\displaystyle \tau }$ on ${\displaystyle X}$ (specifically, ${\displaystyle \tau :=\{\operatorname {int} A:A\subseteq X\}}$) such that for every ${\displaystyle A\subseteq X,}$ ${\displaystyle \operatorname {int} A}$ is equal to the topological interior ${\displaystyle \operatorname {int} _{(X,\tau )}A}$ of ${\displaystyle A}$ in ${\displaystyle (X,\tau ).}$ If the sets ${\displaystyle X}$ and ${\displaystyle Y}$ are each associated with interior operators (both denoted by ${\displaystyle \operatorname {int} }$) then a map ${\displaystyle f:X\to Y}$ is continuous if and only if ${\displaystyle f^{-1}(\operatorname {int} B)\subseteq \operatorname {int} \left(f^{-1}(B)\right)}$ for every subset ${\displaystyle B\subseteq Y.}$^[18]

Filters and prefilters

Main article: Filters in topology

Continuity can also be characterized in terms of filters. A function ${\displaystyle f:X\to Y}$ is continuous if and only if whenever a filter ${\displaystyle {\mathcal {B}}}$ on ${\displaystyle X}$

converges

in ${\displaystyle X}$ to a point ${\displaystyle x\in X,}$ then the

prefilter

${\displaystyle f({\mathcal {B}})}$ converges in ${\displaystyle Y}$ to ${\displaystyle f(x).}$ This characterization remains true if the word "filter" is replaced by "prefilter."^[16]

Properties

If ${\displaystyle f:X\to Y}$ and ${\displaystyle g:Y\to Z}$ are continuous, then so is the composition ${\displaystyle g\circ f:X\to Z.}$ If ${\displaystyle f:X\to Y}$ is continuous and

• X is compact, then f(X) is compact.
• X is connected, then f(X) is connected.
• X is
  path-connected
  , then f(X) is path-connected.
• X is Lindelöf, then f(X) is Lindelöf.
• X is separable, then f(X) is separable.

The possible topologies on a fixed set X are

partially ordered

: a topology ${\displaystyle \tau _{1}}$ is said to be coarser than another topology ${\displaystyle \tau _{2}}$ (notation: ${\displaystyle \tau _{1}\subseteq \tau _{2}}$) if every open subset with respect to ${\displaystyle \tau _{1}}$ is also open with respect to ${\displaystyle \tau _{2}.}$ Then, the identity map $${\displaystyle \operatorname {id} _{X}:\left(X,\tau _{2}\right)\to \left(X,\tau _{1}\right)}$$ is continuous if and only if ${\displaystyle \tau _{1}\subseteq \tau _{2}}$ (see also comparison of topologies). More generally, a continuous function $${\displaystyle \left(X,\tau _{X}\right)\to \left(Y,\tau _{Y}\right)}$$ stays continuous if the topology ${\displaystyle \tau _{Y}}$ is replaced by a coarser topology and/or ${\displaystyle \tau _{X}}$ is replaced by a finer topology.

Homeomorphisms

Symmetric to the concept of a continuous map is an

bijective

function f between two topological spaces, the inverse function ${\displaystyle f^{-1}}$ need not be continuous. A bijective continuous function with a continuous inverse function is called a homeomorphism.

If a continuous bijection has as its domain a compact space and its codomain is Hausdorff, then it is a homeomorphism.

Defining topologies via continuous functions

Given a function $${\displaystyle f:X\to S,}$$ where X is a topological space and S is a set (without a specified topology), the final topology on S is defined by letting the open sets of S be those subsets A of S for which ${\displaystyle f^{-1}(A)}$ is open in X. If S has an existing topology, f is continuous with respect to this topology if and only if the existing topology is

quotient topology under the equivalence relation

defined by f.

Dually, for a function f from a set S to a topological space X, the initial topology on S is defined by designating as an open set every subset A of S such that ${\displaystyle A=f^{-1}(U)}$ for some open subset U of X. If S has an existing topology, f is continuous with respect to this topology if and only if the existing topology is finer than the initial topology on S. Thus, the initial topology is the coarsest topology on S that makes f continuous. If f is injective, this topology is canonically identified with the subspace topology of S, viewed as a subset of X.

A topology on a set S is uniquely determined by the class of all continuous functions ${\displaystyle S\to X}$ into all topological spaces X. Dually, a similar idea can be applied to maps ${\displaystyle X\to S.}$

Related notions

If ${\displaystyle f:S\to Y}$ is a continuous function from some subset ${\displaystyle S}$ of a topological space ${\displaystyle X}$ then a continuous extension of ${\displaystyle f}$ to ${\displaystyle X}$ is any continuous function ${\displaystyle F:X\to Y}$ such that ${\displaystyle F(s)=f(s)}$ for every ${\displaystyle s\in S,}$ which is a condition that often written as ${\displaystyle f=F{\big \vert }_{S}.}$ In words, it is any continuous function ${\displaystyle F:X\to Y}$ that

restricts

to ${\displaystyle f}$ on ${\displaystyle S.}$ This notion is used, for example, in the Tietze extension theorem and the Hahn–Banach theorem. If ${\displaystyle f:S\to Y}$ is not continuous, then it could not possibly have a continuous extension. If ${\displaystyle Y}$ is a Hausdorff space and ${\displaystyle S}$ is a dense subset of ${\displaystyle X}$ then a continuous extension of ${\displaystyle f:S\to Y}$ to ${\displaystyle X,}$ if one exists, will be unique. The Blumberg theorem states that if ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ is an arbitrary function then there exists a dense subset ${\displaystyle D}$ of ${\displaystyle \mathbb {R} }$ such that the restriction ${\displaystyle f{\big \vert }_{D}:D\to \mathbb {R} }$ is continuous; in other words, every function ${\displaystyle \mathbb {R} \to \mathbb {R} }$ can be restricted to some dense subset on which it is continuous.

Various other mathematical domains use the concept of continuity in different but related meanings. For example, in order theory, an order-preserving function ${\displaystyle f:X\to Y}$ between particular types of partially ordered sets ${\displaystyle X}$ and ${\displaystyle Y}$ is continuous if for each directed subset ${\displaystyle A}$ of ${\displaystyle X,}$ we have ${\displaystyle \sup f(A)=f(\sup A).}$ Here ${\displaystyle \,\sup \,}$ is the

supremum

with respect to the orderings in ${\displaystyle X}$ and ${\displaystyle Y,}$ respectively. This notion of continuity is the same as topological continuity when the partially ordered sets are given the

Scott topology.^[19][20]

In category theory, a functor $${\displaystyle F:{\mathcal {C}}\to {\mathcal {D}}}$$ between two

. That is to say, $${\displaystyle \varprojlim _{i\in I}F(C_{i})\cong F\left(\varprojlim _{i\in I}C_{i}\right)}$$ for any small (that is, indexed by a set ${\displaystyle I,}$ as opposed to a

objects

in ${\displaystyle {\mathcal {C}}}$.

A

In

measure theory

, a function ${\displaystyle f:E\to \mathbb {R} ^{k}}$ defined on a

Lebesgue measurable set

${\displaystyle E\subseteq \mathbb {R} ^{n}}$ is called

approximately continuous

at a point ${\displaystyle x_{0}\in E}$ if the approximate limit of ${\displaystyle f}$ at ${\displaystyle x_{0}}$ exists and equals ${\displaystyle f(x_{0})}$. This generalizes the notion of continuity by replacing the ordinary limit with the

See also

• Direction-preserving function - an analog of a continuous function in discrete spaces.

Bibliography

• OCLC 395340485
  .
• "Continuous function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]