Görtler vortices
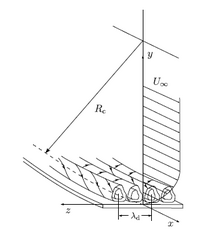
In
radius of curvature
of the wall, the pressure remains constant across the boundary layer. On the other hand, if the boundary layer thickness is comparable to the radius of curvature, the centrifugal action creates a pressure variation across the boundary layer. This leads to the centrifugal instability (Görtler instability) of the boundary layer and consequent formation of Görtler vortices.
Görtler number
The onset of Görtler vortices can be predicted using the
dimensionless number
called Görtler number (G). It is the ratio of centrifugal effects to the viscous effects in the boundary layer and is defined as
where
- = external velocity
- = momentum thickness
- = kinematic viscosity
- = radius of curvature of the wall
Görtler instability occurs when G exceeds about 0.3.
Other instances
A similar phenomenon arising from the same centrifugal action is sometimes observed in rotational flows which do not follow a curved wall, such as the rib vortices seen in the wakes of cylinders[1] and generated behind moving structures.[2]
References
- .
- S2CID 125937677. Retrieved 2 November 2017.
- Görtler, H. (1955). "Dreidimensionales zur Stabilitätstheorie laminarer Grenzschichten". .
- Saric, W. S. (1994). "Görtler vortices". .





