Source: Wikipedia, the free encyclopedia.
Polynomial sequence
In mathematics , Gegenbauer polynomials or ultraspherical polynomials C (α) n x ) are orthogonal polynomials on the interval [−1,1] with respect to the weight function (1 − x 2 )α –1/2Legendre polynomials and Chebyshev polynomials , and are special cases of Jacobi polynomials . They are named after Leopold Gegenbauer .
Characterizations
Plot of the Gegenbauer polynomial C n^(m)(x) with n=10 and m=1 in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
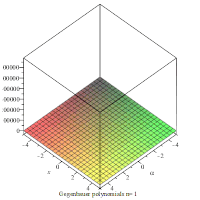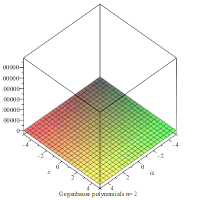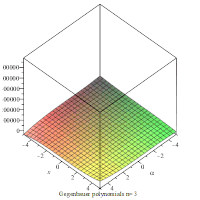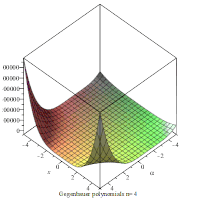
Gegenbauer polynomials with α =1
Gegenbauer polynomials with α =2
Gegenbauer polynomials with α =3
An animation showing the polynomials on the xα -plane for the first 4 values of n .
A variety of characterizations of the Gegenbauer polynomials are available.
1
(
1
−
2
x
t
+
t
2
)
α
=
∑
n
=
0
∞
C
n
(
α
)
(
x
)
t
n
(
0
≤
|
x
|
<
1
,
|
t
|
≤
1
,
α
>
0
)
{\displaystyle {\frac {1}{(1-2xt+t^{2})^{\alpha }}}=\sum _{n=0}^{\infty }C_{n}^{(\alpha )}(x)t^{n}\qquad (0\leq |x|<1,|t|\leq 1,\alpha >0)}
C
0
(
α
)
(
x
)
=
1
C
1
(
α
)
(
x
)
=
2
α
x
(
n
+
1
)
C
n
+
1
(
α
)
(
x
)
=
2
(
n
+
α
)
x
C
n
(
α
)
(
x
)
−
(
n
+
2
α
−
1
)
C
n
−
1
(
α
)
(
x
)
.
{\displaystyle {\begin{aligned}C_{0}^{(\alpha )}(x)&=1\\C_{1}^{(\alpha )}(x)&=2\alpha x\\(n+1)C_{n+1}^{(\alpha )}(x)&=2(n+\alpha )xC_{n}^{(\alpha )}(x)-(n+2\alpha -1)C_{n-1}^{(\alpha )}(x).\end{aligned}}}
Gegenbauer polynomials are particular solutions of the Gegenbauer differential equation (Suetin 2001 ):
(
1
−
x
2
)
y
″
−
(
2
α
+
1
)
x
y
′
+
n
(
n
+
2
α
)
y
=
0.
{\displaystyle (1-x^{2})y''-(2\alpha +1)xy'+n(n+2\alpha )y=0.\,}
When α = 1/2, the equation reduces to the Legendre equation, and the Gegenbauer polynomials reduce to the Legendre polynomials .
When α = 1, the equation reduces to the Chebyshev differential equation, and the Gegenbauer polynomials reduce to the Chebyshev polynomials of the second kind.[1]
C
n
(
α
)
(
z
)
=
(
2
α
)
n
n
!
2
F
1
(
−
n
,
2
α
+
n
;
α
+
1
2
;
1
−
z
2
)
.
{\displaystyle C_{n}^{(\alpha )}(z)={\frac {(2\alpha )_{n}}{n!}}\,_{2}F_{1}\left(-n,2\alpha +n;\alpha +{\frac {1}{2}};{\frac {1-z}{2}}\right).}
(Abramowitz & Stegun p. 561 ). Here (2α)n rising factorial
. Explicitly,
C
n
(
α
)
(
z
)
=
∑
k
=
0
⌊
n
/
2
⌋
(
−
1
)
k
Γ
(
n
−
k
+
α
)
Γ
(
α
)
k
!
(
n
−
2
k
)
!
(
2
z
)
n
−
2
k
.
{\displaystyle C_{n}^{(\alpha )}(z)=\sum _{k=0}^{\lfloor n/2\rfloor }(-1)^{k}{\frac {\Gamma (n-k+\alpha )}{\Gamma (\alpha )k!(n-2k)!}}(2z)^{n-2k}.}
From this it is also easy to obtain the value at unit argument:
C
n
(
α
)
(
1
)
=
Γ
(
2
α
+
n
)
Γ
(
2
α
)
n
!
.
{\displaystyle C_{n}^{(\alpha )}(1)={\frac {\Gamma (2\alpha +n)}{\Gamma (2\alpha )n!}}.}
C
n
(
α
)
(
x
)
=
(
2
α
)
n
(
α
+
1
2
)
n
P
n
(
α
−
1
/
2
,
α
−
1
/
2
)
(
x
)
.
{\displaystyle C_{n}^{(\alpha )}(x)={\frac {(2\alpha )_{n}}{(\alpha +{\frac {1}{2}})_{n}}}P_{n}^{(\alpha -1/2,\alpha -1/2)}(x).}
in which
(
θ
)
n
{\displaystyle (\theta )_{n}}
rising factorial
of
θ
{\displaystyle \theta }
One therefore also has the Rodrigues formula
C
n
(
α
)
(
x
)
=
(
−
1
)
n
2
n
n
!
Γ
(
α
+
1
2
)
Γ
(
n
+
2
α
)
Γ
(
2
α
)
Γ
(
α
+
n
+
1
2
)
(
1
−
x
2
)
−
α
+
1
/
2
d
n
d
x
n
[
(
1
−
x
2
)
n
+
α
−
1
/
2
]
.
{\displaystyle C_{n}^{(\alpha )}(x)={\frac {(-1)^{n}}{2^{n}n!}}{\frac {\Gamma (\alpha +{\frac {1}{2}})\Gamma (n+2\alpha )}{\Gamma (2\alpha )\Gamma (\alpha +n+{\frac {1}{2}})}}(1-x^{2})^{-\alpha +1/2}{\frac {d^{n}}{dx^{n}}}\left[(1-x^{2})^{n+\alpha -1/2}\right].}
Orthogonality and normalization For a fixed α > -1/2 , the polynomials are orthogonal on [−1, 1] with respect to the weighting function (Abramowitz & Stegun p. 774 )
w
(
z
)
=
(
1
−
z
2
)
α
−
1
2
.
{\displaystyle w(z)=\left(1-z^{2}\right)^{\alpha -{\frac {1}{2}}}.}
To wit, for n ≠ m ,
∫
−
1
1
C
n
(
α
)
(
x
)
C
m
(
α
)
(
x
)
(
1
−
x
2
)
α
−
1
2
d
x
=
0.
{\displaystyle \int _{-1}^{1}C_{n}^{(\alpha )}(x)C_{m}^{(\alpha )}(x)(1-x^{2})^{\alpha -{\frac {1}{2}}}\,dx=0.}
They are normalized by
∫
−
1
1
[
C
n
(
α
)
(
x
)
]
2
(
1
−
x
2
)
α
−
1
2
d
x
=
π
2
1
−
2
α
Γ
(
n
+
2
α
)
n
!
(
n
+
α
)
[
Γ
(
α
)
]
2
.
{\displaystyle \int _{-1}^{1}\left[C_{n}^{(\alpha )}(x)\right]^{2}(1-x^{2})^{\alpha -{\frac {1}{2}}}\,dx={\frac {\pi 2^{1-2\alpha }\Gamma (n+2\alpha )}{n!(n+\alpha )[\Gamma (\alpha )]^{2}}}.}
Applications The Gegenbauer polynomials appear naturally as extensions of Legendre polynomials in the context of potential theory and harmonic analysis . The Newtonian potential in R n n − 2)/2,
1
|
x
−
y
|
n
−
2
=
∑
k
=
0
∞
|
x
|
k
|
y
|
k
+
n
−
2
C
k
(
α
)
(
x
⋅
y
|
x
|
|
y
|
)
.
{\displaystyle {\frac {1}{|\mathbf {x} -\mathbf {y} |^{n-2}}}=\sum _{k=0}^{\infty }{\frac {|\mathbf {x} |^{k}}{|\mathbf {y} |^{k+n-2}}}C_{k}^{(\alpha )}({\frac {\mathbf {x} \cdot \mathbf {y} }{|\mathbf {x} ||\mathbf {y} |}}).}
When n = 3, this gives the Legendre polynomial expansion of the gravitational potential . Similar expressions are available for the expansion of the Poisson kernel in a ball (Stein & Weiss 1971 ).
It follows that the quantities
C
k
(
(
n
−
2
)
/
2
)
(
x
⋅
y
)
{\displaystyle C_{k}^{((n-2)/2)}(\mathbf {x} \cdot \mathbf {y} )}
zonal spherical harmonics
, up to a normalizing constant.
Gegenbauer polynomials also appear in the theory of Positive-definite functions .
The Askey–Gasper inequality reads
∑
j
=
0
n
C
j
α
(
x
)
(
2
α
+
j
−
1
j
)
≥
0
(
x
≥
−
1
,
α
≥
1
/
4
)
.
{\displaystyle \sum _{j=0}^{n}{\frac {C_{j}^{\alpha }(x)}{2\alpha +j-1 \choose j}}\geq 0\qquad (x\geq -1,\,\alpha \geq 1/4).}
In
banded matrix methods for large problems.
[2] See also References Specific
^ Arfken, Weber, and Harris (2013) "Mathematical Methods for Physicists", 7th edition; ch. 18.4
. 
Plot of the Gegenbauer polynomial C n^(m)(x) with n=10 and m=1 in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Gegenbauer polynomials with α=1
Gegenbauer polynomials with α=2
Gegenbauer polynomials with α=3
An animation showing the polynomials on the xα-plane for the first 4 values of n.(x)_with_n%3D10_and_m%3D1_in_the_complex_plane_from_-2-2i_to_2%2B2i_with_colors_created_with_Mathematica_13.1_function_ComplexPlot3D.svg)
![{\displaystyle C_{n}^{(\alpha )}(x)={\frac {(-1)^{n}}{2^{n}n!}}{\frac {\Gamma (\alpha +{\frac {1}{2}})\Gamma (n+2\alpha )}{\Gamma (2\alpha )\Gamma (\alpha +n+{\frac {1}{2}})}}(1-x^{2})^{-\alpha +1/2}{\frac {d^{n}}{dx^{n}}}\left[(1-x^{2})^{n+\alpha -1/2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7380d774285ba35cc371daa8be46e38b2442eca1)
![{\displaystyle \int _{-1}^{1}\left[C_{n}^{(\alpha )}(x)\right]^{2}(1-x^{2})^{\alpha -{\frac {1}{2}}}\,dx={\frac {\pi 2^{1-2\alpha }\Gamma (n+2\alpha )}{n!(n+\alpha )[\Gamma (\alpha )]^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9b5696990f291fed55949f3b9e2f1669b9f4c83)
