Gnomonic projection
This article includes a improve this article by introducing more precise citations. (February 2019) ) |


A gnomonic projection, also known as a central projection or rectilinear projection, is a
The projection is the n-dimensional generalization of the
The gnomonic projection is
The gnomonic projection originated in astronomy for constructing sundials and charting the celestial sphere. It is commonly used as a geographic map projection, and can be convenient in navigation because great-circle courses are plotted as straight lines. Rectilinear photographic lenses make a perspective projection of the world onto an image plane; this can be thought of as a gnomonic projection of the image sphere (an abstract sphere indicating the direction of each ray passing through a camera modeled as a pinhole). The gnomonic projection is used in crystallography for analyzing the orientations of lines and planes of crystal structures. It is used in structural geology for analyzing the orientations of fault planes. In computer graphics and computer representation of spherical data, cube mapping is the gnomonic projection of the image sphere onto six faces of a cube.
In mathematics, the space of
History
The gnomonic
Properties
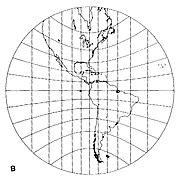
The gnomonic projection is from the centre of a sphere to a plane tangent to the sphere (Fig 1 below). The sphere and the plane touch at the tangent point. Great circles transform to straight lines via the gnomonic projection. Since meridians (lines of longitude) and the equator are great circles, they are always shown as straight lines on a gnomonic map. Since the projection is from the centre of the sphere, a gnomonic map can represent less than half of the area of the sphere. Distortion of the scale of the map increases from the centre (tangent point) to the periphery.[2]
- If the tangent point is one of the poles then the meridians are radial and equally spaced (Fig 2 below). The equator cannot be shown as it is at infinity in all directions. Other parallels (lines of latitude) are depicted as concentric circles.
- If the tangent point is on the equator then the meridians are parallel but not equally spaced (Fig 3 below). The equator is a straight line perpendicular to the meridians. Other parallels are depicted as hyperbolae.
- If the tangent point is not on a pole or the equator, then the meridians are radially outward straight lines from a pole, but not equally spaced (Fig 4 below). The equator is a straight line that is perpendicular to only one meridian, indicating that the projection is not conformal. Other parallels are depicted as conic sections.
As with all azimuthal projections, angles from the tangent point are preserved. The map distance from that point is a function r(d) of the true distance d, given by
where R is the radius of the Earth. The radial scale is
and the transverse scale
so the transverse scale increases outwardly, and the radial scale even more.
Use

Gnomonic projections are used in
The gnomonic projection is used extensively in photography, where it is called rectilinear projection, as it naturally arises from the pinhole camera model where the screen is a plane.[3] Because they are equivalent, the same viewer used for photographic panoramas can be used to render gnomonic maps (view as a 360° interactive panorama).
The gnomonic projection is used in astronomy where the tangent point is centered on the object of interest. The sphere being projected in this case is the celestial sphere, R = 1, and not the surface of the Earth.
In astronomy, gnomic projection star charts of the
See also
- Local tangent plane
- List of map projections
- Beltrami–Klein model, the analogous mapping of the hyperbolic plane
References
- .
- ^ doi:10.3133/pp1395.
- ISBN 978-1-315-39521-0.
- ISBN 9783319445182.
Further reading
- Amorós, José Luis; Buerger, Martin J.; Canut de Amorós, Marisa (1975). "3. The gnomonic projection". The Laue Method. Academic Press. pp. 55–81. .
- Calabretta, Mark R.; Greisen, Eric W. (2002). "Representations of celestial coordinates in FITS (Paper II)". Astronomy & Astrophysics. 395: 1077–1122. .
- Boeke, Hendrik Enno (1913). Die gnomonische Projektion in ihrer Anwendung auf kristallographische Aufgaben [The gnomonic projection in its application to crystallographic tasks] (in German). Gebrüder Borntraeger.
- Bradley, A.D. (1940). "The Gnomonic Projection of the Sphere". American Mathematical Monthly. 47 (10): 694–699. JSTOR 2302492.
- De Morgan, Augustus (1836). An explanation of the Gnomonic Projection of the Sphere. Baldwin & Cradock.
- Günther, S. (1883). "Die gnomonische Kartenprojektion" [The gnomonic map projection]. Zeitschrift der Gesellschaft für Erdkunde zu Berlin (in German). 18: 137–149.
- Herbert Smith, G. F. (1903). "On the Advantages of the Gnomonic Projection and Its Use in the Drawing of Crystals" (PDF). Mineralogical Magazine. 13 (62): 309–322. .
- Hilton, Harold (1904). "The Gnomonic Net" (PDF). Mineralogical Magazine. 14 (63): 18–20. .
- Palache, Charles (1920). "The gnomonic projection" (PDF). American Mineralogist. 5 (4): 67–80.
- Pye, Norman (1950). "The Oblique Gnomonic Projection". Empire Survey Review. 10 (75): 227–232. .
- Rogers, Austin F. (1907). "The Gnomonic Projection from a Graphical Standpoint". School of Mines Quarterly. 29 (1): 24–33.