Halin graph

This is a good article. Click here for more information.
Source: Wikipedia, the free encyclopedia.

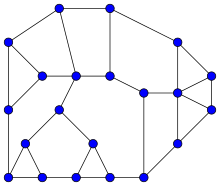
A Halin graph with 21 vertices
A Halin graph

In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the

planar embedding
), and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.[1]

Halin graphs are named after German mathematician Rudolf Halin, who studied them in 1971.[2] The cubic Halin graphs – the ones in which each vertex touches exactly three edges – had already been studied over a century earlier by Kirkman.[3] Halin graphs are

convex polyhedron
, and the polyhedra formed from them have been called roofless polyhedra or domes.

Every Halin graph has a

linear time. Because Halin graphs have low treewidth
, many computational problems that are hard on other kinds of planar graphs, such as finding Hamiltonian cycles, can be solved quickly on Halin graphs.

The graph of a triangular prism
A triangular prism, constructed as a Halin graph from a six-vertex tree

Examples

Wheel graphs with four to nine vertices
Wheel graphs

A star is a tree with exactly one internal vertex. Applying the Halin graph construction to a star produces a wheel graph, the graph of the (edges of) a pyramid.[4] The graph of a triangular prism is also a Halin graph: it can be drawn so that one of its rectangular faces is the exterior cycle, and the remaining edges form a tree with four leaves, two interior vertices, and five edges.[5]

The Frucht graph, one of the five smallest cubic graphs with no nontrivial graph automorphisms,[6] is also a Halin graph.[7]

Properties

Every Halin graph is

convex polyhedron; that is, it is a polyhedral graph. The polyhedron that realizes the graph can be chosen so that the face containing all of the tree leaves is horizontal, and all of the other faces lie above it, with equal slopes.[8] As with every polyhedral graph, Halin graphs have a unique planar embedding, up to the choice of which of its faces is to be the outer face.[1]

Every Halin graph is a

Hamiltonian cycle. Moreover, any Halin graph remains Hamiltonian after the deletion of any vertex.[9]
Because every tree without vertices of degree 2 contains two leaves that share the same parent, every Halin graph contains a triangle. In particular, it is not possible for a Halin graph to be a triangle-free graph nor a bipartite graph.[10]

Halin graph with one 16-vertex face, two 10-vertex faces, and all other faces having 3 to 5 vertices
A Halin graph without any 8-cycles. A similar construction allows any single even cycle length to be avoided.[11]

More strongly, every Halin graph is almost pancyclic, in the sense that it has cycles of all lengths from 3 to n with the possible exception of a single even length. Moreover, any Halin graph remains almost pancyclic if a single edge is contracted, and every Halin graph without interior vertices of degree three is pancyclic.[12]

The incidence chromatic number of a Halin graph G with maximum degree Δ(G) greater than four is Δ(G) + 1.[13] This is the number of colors needed to color all pairs (v,e) where v is a vertex of the graph, and e is an edge incident to v, obeying certain constraints on the coloring. Pairs that share a vertex or that share an edge are not allowed to have the same color. In addition, a pair (v,e) cannot have the same color as another pair that uses the other endpoint of e. For Halin graphs with Δ(G) = 3 or 4, the incidence chromatic number may be as large as 5 or 6 respectively.[14]

Computational complexity

It is possible to test whether a given n-vertex graph is a Halin graph in

linear time, by finding a planar embedding of the graph (if one exists), and then testing whether there exists a face that has at least n/2 + 1 vertices, all of degree three. If so, there can be at most four such faces, and it is possible to check in linear time for each of them whether the rest of the graph forms a tree with the vertices of this face as its leaves. On the other hand, if no such face exists, then the graph is not Halin.[15] Alternatively, a graph with n vertices and m edges is Halin if and only if it is planar, 3-connected, and has a face whose number of vertices equals the circuit rank m − n + 1 of the graph, all of which can be checked in linear time.[16] Other methods for recognizing Halin graphs in linear time include the application of Courcelle's theorem, or a method based on graph rewriting, neither of which rely on knowing the planar embedding of the graph.[17]

Every Halin graph has

Hamiltonian cycles) by direct algorithms.[17]
However, it is
NP-complete to find the largest Halin subgraph of a given graph, to test whether there exists a Halin subgraph that includes all vertices of a given graph, or to test whether a given graph is a subgraph of a larger Halin graph.[20]

History

In 1971, Halin introduced the Halin graphs as a class of

minimally 3-vertex-connected graphs: for every edge in the graph, the removal of that edge reduces the connectivity of the graph.[2] These graphs gained significance with the discovery that many algorithmic problems that were computationally infeasible for arbitrary planar graphs could be solved efficiently on them.[9][16] This fact was later explained to be a consequence of their low treewidth, and of algorithmic meta-theorems like Courcelle's theorem that provide efficient solutions to these problems on any graph of low treewidth.[18][19]

Prior to Halin's work on these graphs, graph enumeration problems concerning the cubic (or 3-regular) Halin graphs were studied in 1856 by Thomas Kirkman[3] and in 1965 by Hans Rademacher. Rademacher calls these graphs based polyhedra. He defines them as the cubic polyhedral graphs with f faces in which one of the faces has f − 1 sides.[21] The graphs that fit this definition are exactly the cubic Halin graphs.[22]

Inspired by the fact that both Halin graphs and 4-vertex-connected planar graphs contain Hamiltonian cycles, Lovász & Plummer (1974) conjectured that every 4-vertex-connected planar graph contains a spanning Halin subgraph; here "spanning" means that the subgraph includes all vertices of the larger graph. The Lovász–Plummer conjecture remained open until 2015, when a construction for infinitely many counterexamples was published.[23]

The Halin graphs are sometimes also called skirted trees

convex polyhedra whose graphs are Halin graphs have also been called domes.[25]

References

  1. ^
    ISBN 0-7923-4709-9, p. 281, article "Halin Graph"
    , and references therein.
  2. ^
    MR 0278980
    .
  3. ^
    JSTOR 108592
    .
  4. ^ Cornuéjols, Naddef & Pulleyblank (1983): "If T is a star, i.e., a single node v joined to n other nodes, then H is called a wheel and is the simplest type of Halin graph."
  5. ^ See Sysło & Proskurowski (1983), Prop. 4.3, p. 254, which identifies the triangular prism as the unique graph with exactly three cycles that can be the outer cycle of a realization as a Halin graph.
  6. ^ Bussemaker, F. C.; Cobeljic, S.; Cvetkovic, D. M.; Seidel, J. J. (1976), "Computer investigation of cubic graphs", Eindhoven University of Technology Research Portal, EUT report, 76-WSK-01, Dept. of Mathematics and Computing Science, Eindhoven University of Technology
  7. ^ Weisstein, Eric W., "Halin Graph", MathWorld
  8. ^ Aichholzer, Oswin; Cheng, Howard; Devadoss, Satyan L.; Hackl, Thomas; Huber, Stefan; Li, Brian; Risteski, Andrej (2012), "What makes a tree a straight skeleton?" (PDF), Proceedings of the 24th Canadian Conference on Computational Geometry (CCCG'12)
  9. ^
    S2CID 26278382
    .
  10. S2CID 26975523
    : "Since G contains a 3-cycle consisting of one inner vertex and two outer vertices, G is not a bipartite graph."
  11. ^
    MR 0491287
  12. ^ Skowrońska, Mirosława (1985), "The pancyclicity of Halin graphs and their exterior contractions", in Alspach, Brian R.; Godsil, Christopher D. (eds.), Cycles in Graphs, Annals of Discrete Mathematics, vol. 27, Elsevier Science Publishers B.V., pp. 179–194.
  13. MR 1927561
    .
  14. MR 2466963
    .
  15. MR 2577677
    .
  16. ^
    doi:10.1007/BFb0071635
    .
  17. ^
    S2CID 9525753
    .
  18. ^ a b Bodlaender, Hans (1988), Planar graphs with bounded treewidth (PDF), Technical Report RUU-CS-88-14, Department of Computer Science, Utrecht University, archived from the original (PDF) on 2004-07-28.
  19. ^
    ISBN 978-3540194880
    .
  20. MR 1311302
    .
  21. MR 0179682
    .
  22. ^
    MR 0351915
    .
  23. MR 3376776
    .
  24. MR 0951375
  25. ^ Demaine, Erik D.; Demaine, Martin L.; Uehara, Ryuhei (2013), "Zipper unfolding of domes and prismoids", Proceedings of the 25th Canadian Conference on Computational Geometry (CCCG 2013), Waterloo, Ontario, Canada, August 8–10, 2013, pp. 43–48.

External links

Retrieved from "https://en.wikipedia.org/w/index.php?title=Halin_graph&oldid=1173837482"