Knot (mathematics)

Source: Wikipedia, the free encyclopedia.
This article is about the mathematical object. For other uses, see Knot (disambiguation).
A table of all prime knots with seven crossings or fewer (not including mirror images)
An overhand knot becomes a trefoil knot by joining the ends.
The triangle is associated with the trefoil knot.
Pretzel bread in the shape of a 74 pretzel knot

In mathematics, a knot is an embedding of the circle (S1) into three-dimensional Euclidean space, R3 (also known as E3). Often two knots are considered equivalent if they are ambient isotopic, that is, if there exists a continuous deformation of R3 which takes one knot to the other.

A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed — there are no ends to tie or untie on a mathematical knot. Physical properties such as friction and thickness also do not apply, although there are mathematical definitions of a knot that take such properties into account. The term knot is also applied to embeddings of S j in Sn, especially in the case j = n − 2. The branch of mathematics that studies knots is known as knot theory and has many relations to graph theory.

Formal definition

A knot is an embedding of the circle (S1) into three-dimensional Euclidean space (R3),[1] or the 3-sphere (S3), since the 3-sphere is compact.[2] [Note 1] Two knots are defined to be equivalent if there is an ambient isotopy between them.[3]

Projection

A knot in

Reidemeister moves
.

  • Reidemeister move 1
    Reidemeister move 1
  • Reidemeister move 2
    Reidemeister move 2
  • Reidemeister move 3
    Reidemeister move 3

Types of knots

A knot can be untied if the loop is broken.

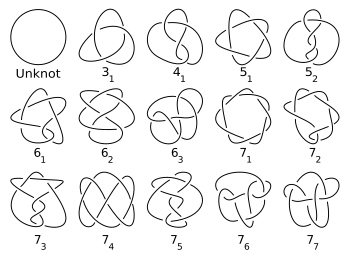
The simplest knot, called the unknot or trivial knot, is a round circle embedded in R3.[4] In the ordinary sense of the word, the unknot is not "knotted" at all. The simplest nontrivial knots are the trefoil knot (31 in the table), the figure-eight knot (41) and the cinquefoil knot (51).[5]

Several knots, linked or tangled together, are called links. Knots are links with a single component.

Tame vs. wild knots

A wild knot

A polygonal knot is a knot whose

line segments.[6] A tame knot is any knot equivalent to a polygonal knot.[6][Note 2] Knots which are not tame are called wild,[7] and can have pathological behavior.[7] In knot theory and 3-manifold
theory, often the adjective "tame" is omitted. Smooth knots, for example, are always tame.

Framed knot

A framed knot is the extension of a tame knot to an embedding of the solid torus D2 × S1 in S3.

The framing of the knot is the linking number of the image of the ribbon I × S1 with the knot. A framed knot can be seen as the embedded ribbon and the framing is the (signed) number of twists.[8] This definition generalizes to an analogous one for framed links. Framed links are said to be equivalent if their extensions to solid tori are ambient isotopic.

Framed link diagrams are link diagrams with each component marked, to indicate framing, by an integer representing a slope with respect to the meridian and preferred longitude. A standard way to view a link diagram without markings as representing a framed link is to use the blackboard framing. This framing is obtained by converting each component to a ribbon lying flat on the plane. A type I Reidemeister move clearly changes the blackboard framing (it changes the number of twists in a ribbon), but the other two moves do not. Replacing the type I move by a modified type I move gives a result for link diagrams with blackboard framing similar to the Reidemeister theorem: Link diagrams, with blackboard framing, represent equivalent framed links if and only if they are connected by a sequence of (modified) type I, II, and III moves. Given a knot, one can define infinitely many framings on it. Suppose that we are given a knot with a fixed framing. One may obtain a new framing from the existing one by cutting a ribbon and twisting it an integer multiple of 2π around the knot and then glue back again in the place we did the cut. In this way one obtains a new framing from an old one, up to the equivalence relation for framed knots„ leaving the knot fixed. [9] The framing in this sense is associated to the number of twists the vector field performs around the knot. Knowing how many times the vector field is twisted around the knot allows one to determine the vector field up to diffeomorphism, and the equivalence class of the framing is determined completely by this integer called the framing integer.

Knot complement

A knot whose complement has a non-trivial JSJ decomposition

Given a knot in the 3-sphere, the

3-manifold theory.[10]

JSJ decomposition

Main article: JSJ decomposition

The JSJ decomposition and Thurston's hyperbolization theorem reduces the study of knots in the 3-sphere to the study of various geometric manifolds via splicing or satellite operations. In the pictured knot, the JSJ-decomposition splits the complement into the union of three manifolds: two trefoil complements and the complement of the Borromean rings. The trefoil complement has the geometry of H2 × R, while the Borromean rings complement has the geometry of H3.

Harmonic knots

Parametric representations of knots are called harmonic knots. Aaron Trautwein compiled parametric representations for all knots up to and including those with a crossing number of 8 in his PhD thesis.[11][12]

Applications to graph theory

knot diagrams with their medial graph

Medial graph

Main article: Medial graph
The signed planar graph associated with a knot diagram.
Left guide
Right guide

Another convenient representation of knot diagrams

Peter Tait in 1877.[15][16]

Any knot diagram defines a

homeomorphic to a 2-dimensional disk. Color these faces black or white so that the unbounded face is black and any two faces that share a boundary edge have opposite colors. The Jordan curve theorem
implies that there is exactly one such coloring.

We construct a new plane graph whose vertices are the white faces and whose edges correspond to crossings. We can label each edge in this graph as a left edge or a right edge, depending on which thread appears to go over the other as we view the corresponding crossing from one of the endpoints of the edge. Left and right edges are typically indicated by labeling left edges + and right edges –, or by drawing left edges with solid lines and right edges with dashed lines.

The original knot diagram is the medial graph of this new plane graph, with the type of each crossing determined by the sign of the corresponding edge. Changing the sign of every edge corresponds to reflecting the knot in a mirror.

Linkless and knotless embedding

Main article: linkless embedding
The seven graphs in the Petersen family. No matter how these graphs are embedded into three-dimensional space, some two cycles will have nonzero linking number.

In two dimensions, only the

knotless embeddings. A linkless embedding is an embedding of the graph with the property that any two cycles are unlinked; a knotless embedding is an embedding of the graph with the property that any single cycle is unknotted. The graphs that have linkless embeddings have a forbidden graph characterization involving the Petersen family, a set of seven graphs that are intrinsically linked: no matter how they are embedded, some two cycles will be linked with each other.[17] A full characterization of the graphs with knotless embeddings is not known, but the complete graph K7 is one of the minimal forbidden graphs for knotless embedding: no matter how K7 is embedded, it will contain a cycle that forms a trefoil knot.[18]

Generalization

In contemporary mathematics the term knot is sometimes used to describe a more general phenomenon related to embeddings. Given a manifold M with a submanifold N, one sometimes says N can be knotted in M if there exists an embedding of N in M which is not isotopic to N. Traditional knots form the case where N = S1 and M = R3 or M = S3.[19][20]

The

Schoenflies theorem states that the circle does not knot in the 2-sphere: every topological circle in the 2-sphere is isotopic to a geometric circle.[21] Alexander's theorem states that the 2-sphere does not smoothly (or PL or tame topologically) knot in the 3-sphere.[22] In the tame topological category, it's known that the n-sphere does not knot in the n + 1-sphere for all n. This is a theorem of Morton Brown, Barry Mazur, and Marston Morse.[23] The Alexander horned sphere is an example of a knotted 2-sphere in the 3-sphere which is not tame.[24] In the smooth category, the n-sphere is known not to knot in the n + 1-sphere provided n ≠ 3. The case n = 3 is a long-outstanding problem closely related to the question: does the 4-ball admit an exotic smooth structure
?

André Haefliger proved that there are no smooth j-dimensional knots in Sn provided 2n − 3j − 3 > 0, and gave further examples of knotted spheres for all n > j ≥ 1 such that 2n − 3j − 3 = 0. n − j is called the codimension of the knot. An interesting aspect of Haefliger's work is that the isotopy classes of embeddings of S j in Sn form a group, with group operation given by the connect sum, provided the co-dimension is greater than two. Haefliger based his work on Stephen Smale's h-cobordism theorem. One of Smale's theorems is that when one deals with knots in co-dimension greater than two, even inequivalent knots have diffeomorphic complements. This gives the subject a different flavour than co-dimension 2 knot theory. If one allows topological or PL-isotopies, Christopher Zeeman proved that spheres do not knot when the co-dimension is greater than 2. See a generalization to manifolds.

See also

Notes

  1. one-point compactification
    ).
  2. ^ A knot is tame if and only if it can be represented as a finite closed polygonal chain

References

  1. ^ Armstrong (1983), p. 213.
  2. ^ Cromwell 2004, p. 33; Adams 1994, pp. 246–250
  3. ^ Cromwell (2004), p. 5.
  4. ^ Adams (1994), p. 2.
  5. ^ Adams 1994, Table 1.1, p. 280; Livingstone 1993, Appendix A: Knot Table, p. 221
  6. ^ a b Armstrong 1983, p. 215
  7. ^
    ISBN 978-0-88385-027-5
    .
  8. doi:10.1090/S0002-9947-1990-0958895-7
    .
  9. arXiv:1910.10257
    .
  10. ^ Adams 1994, pp. 261–2
  11. ProQuest 304216894
    .
  12. ISBN 978-981-02-3530-7
    .
  13. ISBN 978-0-8218-3678-1
    .
  14. ^ Entrelacs.net tutorial
  15. doi:10.1017/S0080456800090633
    . Revised May 11, 1877.
  16. doi:10.1017/S0370164600032363
    .
  17. ^ Robertson, Neil; Seymour, Paul; Thomas, Robin (1993), "A survey of linkless embeddings", in Robertson, Neil; Seymour, Paul (eds.), Graph Structure Theory: Proc. AMS–IMS–SIAM Joint Summer Research Conference on Graph Minors (PDF), Contemporary Mathematics, vol. 147, American Mathematical Society, pp. 125–136.
  18. doi:10.1007/PL00009446
    .
  19. MR 1487374
    .
  20. MR 3588325
    .
  21. MR 1016814
    .
  22. MR 2327361
    .
  23. MR 0117694
    .
  24. PMID 16576780
    .

Bibliography

External links

Wikimedia Commons has media related to Knots (knot theory).
Retrieved from "https://en.wikipedia.org/w/index.php?title=Knot_(mathematics)&oldid=1195004148"