Compact space

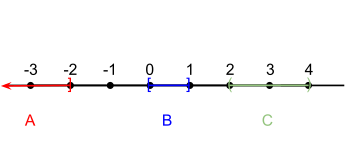
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space.^[1] The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all limiting values of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval [0,1] would be compact. Similarly, the space of rational numbers ${\displaystyle \mathbb {Q} }$ is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers ${\displaystyle \mathbb {R} }$ is not compact either, because it excludes the two limiting values ${\displaystyle +\infty }$ and ${\displaystyle -\infty }$. However, the

.

One such generalization is that a topological space is

[0, 1], some of those points will get arbitrarily close to some real number in that space. For instance, some of the numbers in the sequence 1/2, 4/5, 1/3, 5/6, 1/4, 6/7, ... accumulate to 0 (while others accumulate to 1). Since neither 0 nor 1 are members of the open unit interval (0, 1), those same sets of points would not accumulate to any point of it, so the open unit interval is not compact. Although subsets (subspaces) of Euclidean space can be compact, the entire space itself is not compact, since it is not bounded. For example, considering ${\displaystyle \mathbb {R} ^{1}}$ (the real number line), the sequence of points 0,  1,  2,  3, ... has no subsequence that converges to any real number.

Compactness was formally introduced by

– that is, in a neighborhood of each point – into corresponding statements that hold throughout the space, and many theorems are of this character.

The term compact set is sometimes used as a synonym for compact space, but also often refers to a compact subspace of a topological space.

Historical development

In the 19th century, several disparate mathematical properties were understood that would later be seen as consequences of compactness. On the one hand,

. Bolzano's proof relied on the : the sequence was placed into an interval that was then divided into two equal parts, and a part containing infinitely many terms of the sequence was selected. The process could then be repeated by dividing the resulting smaller interval into smaller and smaller parts – until it closes down on the desired limit point. The full significance of Bolzano's theorem, and its method of proof, would not emerge until almost 50 years later when it was rediscovered by Karl Weierstrass.^[4]

In the 1880s, it became clear that results similar to the Bolzano–Weierstrass theorem could be formulated for spaces of functions rather than just numbers or geometrical points. The idea of regarding functions as themselves points of a generalized space dates back to the investigations of Giulio Ascoli and Cesare Arzelà.^[5] The culmination of their investigations, the Arzelà–Ascoli theorem, was a generalization of the Bolzano–Weierstrass theorem to families of continuous functions, the precise conclusion of which was that it was possible to extract a uniformly convergent sequence of functions from a suitable family of functions. The uniform limit of this sequence then played precisely the same role as Bolzano's "limit point". Towards the beginning of the twentieth century, results similar to that of Arzelà and Ascoli began to accumulate in the area of integral equations, as investigated by David Hilbert and Erhard Schmidt. For a certain class of

as an offshoot of the general notion of a compact space. It was which led to the famous 1906 thesis).

However, a different notion of compactness altogether had also slowly emerged at the end of the 19th century from the study of the continuum, which was seen as fundamental for the rigorous formulation of analysis. In 1870,

. In the course of the proof, he made use of a lemma that from any countable cover of the interval by smaller open intervals, it was possible to select a finite number of these that also covered it. The significance of this lemma was recognized by Émile Borel (1895), and it was generalized to arbitrary collections of intervals by Pierre Cousin (1895) and Henri Lebesgue (1904). The Heine–Borel theorem, as the result is now known, is another special property possessed by closed and bounded sets of real numbers.

This property was significant because it allowed for the passage from

, under appropriate conditions followed from the version of compactness that was formulated in terms of the existence of finite subcovers. It was this notion of compactness that became the dominant one, because it was not only a stronger property, but it could be formulated in a more general setting with a minimum of additional technical machinery, as it relied only on the structure of the open sets in a space.

Basic examples

Any finite space is compact; a finite subcover can be obtained by selecting, for each point, an open set containing it. A nontrivial example of a compact space is the (closed) unit interval [0,1] of real numbers. If one chooses an infinite number of distinct points in the unit interval, then there must be some accumulation point among these points in that interval. For instance, the odd-numbered terms of the sequence 1, 1/2, 1/3, 3/4, 1/5, 5/6, 1/7, 7/8, ... get arbitrarily close to 0, while the even-numbered ones get arbitrarily close to 1. The given example sequence shows the importance of including the boundary points of the interval, since the limit points must be in the space itself — an open (or half-open) interval of the real numbers is not compact. It is also crucial that the interval be bounded, since in the interval [0,∞), one could choose the sequence of points 0, 1, 2, 3, ..., of which no sub-sequence ultimately gets arbitrarily close to any given real number.

In two dimensions, closed disks are compact since for any infinite number of points sampled from a disk, some subset of those points must get arbitrarily close either to a point within the disc, or to a point on the boundary. However, an open disk is not compact, because a sequence of points can tend to the boundary – without getting arbitrarily close to any point in the interior. Likewise, spheres are compact, but a sphere missing a point is not since a sequence of points can still tend to the missing point, thereby not getting arbitrarily close to any point within the space. Lines and planes are not compact, since one can take a set of equally-spaced points in any given direction without approaching any point.

Definitions

Various definitions of compactness may apply, depending on the level of generality. A subset of

In contrast, the different notions of compactness are not equivalent in general topological spaces, and the most useful notion of compactness – originally called bicompactness – is defined using covers consisting of open sets (see Open cover definition below). That this form of compactness holds for closed and bounded subsets of Euclidean space is known as the

; here, continuity is a local property of the function, and uniform continuity the corresponding global property.

Open cover definition

Formally, a

of X such that

$${\displaystyle X=\bigcup _{S\in C}S\ ,}$$

there is a finite subcollection F ⊆ C such that

$${\displaystyle X=\bigcup _{S\in F}S\ .}$$

Some branches of mathematics such as algebraic geometry, typically influenced by the French school of Bourbaki, use the term quasi-compact for the general notion, and reserve the term compact for topological spaces that are both Hausdorff and quasi-compact. A compact set is sometimes referred to as a compactum, plural compacta.

Compactness of subsets

A subset K of a topological space X is said to be compact if it is compact as a subspace (in the subspace topology). That is, K is compact if for every arbitrary collection C of open subsets of X such that

there is a finite subcollection F ⊆ C such that

Compactness is a topological property. That is, if ${\displaystyle K\subset Z\subset Y}$, with subset Z equipped with the subspace topology, then K is compact in Z if and only if K is compact in Y.

Characterization

If X is a topological space then the following are equivalent:

1. X is compact; i.e., every
   subcover
   .
2. X has a sub-base such that every cover of the space, by members of the sub-base, has a finite subcover (
   Alexander's sub-base theorem
   ).
3. X is
   countably compact.^[9]
4. Any collection of closed subsets of X with the finite intersection property has nonempty intersection.
5. Every net on X has a convergent subnet (see the article on nets for a proof).
6. Every filter on X has a convergent refinement.
7. Every net on X has a cluster point.
8. Every filter on X has a cluster point.
9. Every
   ultrafilter
   on X converges to at least one point.
10. Every infinite subset of X has a
    complete accumulation point.^[10]
11. For every topological space Y, the projection ${\displaystyle X\times Y\to Y}$ is a
    closed mapping^[11] (see proper map
    ).
12. Every open cover linearly ordered by subset inclusion contains X.[12]

Bourbaki defines a compact space (quasi-compact space) as a topological space where each filter has a cluster point (i.e., 8. in the above).^[13]

Euclidean space

For any subset A of Euclidean space, A is compact if and only if it is closed and bounded; this is the Heine–Borel theorem.

As a Euclidean space is a metric space, the conditions in the next subsection also apply to all of its subsets. Of all of the equivalent conditions, it is in practice easiest to verify that a subset is closed and bounded, for example, for a closed interval or closed n-ball.

Metric spaces

For any metric space (X, d), the following are equivalent (assuming

):

1. (X, d) is compact.
2. (X, d) is
   totally bounded (this is also equivalent to compactness for uniform spaces).^[14]
3. (X, d) is sequentially compact; that is, every
   first-countable uniform spaces
   ).
4. (X, d) is
   limit point
   in X.
5. (X, d) is
   countably compact
   ; that is, every countable open cover of X has a finite subcover.
6. (X, d) is an image of a continuous function from the Cantor set.^[15]
7. Every decreasing nested sequence of nonempty closed subsets S₁ ⊇ S₂ ⊇ ... in (X, d) has a nonempty intersection.
8. Every increasing nested sequence of proper open subsets S₁ ⊆ S₂ ⊆ ... in (X, d) fails to cover X.

A compact metric space (X, d) also satisfies the following properties:

1. Lebesgue's number lemma: For every open cover of X, there exists a number δ > 0 such that every subset of X of diameter < δ is contained in some member of the cover.
2. (X, d) is second-countable, separable and Lindelöf – these three conditions are equivalent for metric spaces. The converse is not true; e.g., a countable discrete space satisfies these three conditions, but is not compact.
3. X is closed and bounded (as a subset of any metric space whose restricted metric is d). The converse may fail for a non-Euclidean space; e.g. the
   discrete metric is closed and bounded but not compact, as the collection of all singletons
   of the space is an open cover which admits no finite subcover. It is complete but not totally bounded.

Ordered spaces

For an ordered space (X, <) (i.e. a totally ordered set equipped with the order topology), the following are equivalent:

1. (X, <) is compact.
2. Every subset of X has a supremum (i.e. a least upper bound) in X.
3. Every subset of X has an infimum (i.e. a greatest lower bound) in X.
4. Every nonempty closed subset of X has a maximum and a minimum element.

An ordered space satisfying (any one of) these conditions is called a complete lattice.

In addition, the following are equivalent for all ordered spaces (X, <), and (assuming

countable choice

) are true whenever (X, <) is compact. (The converse in general fails if (X, <) is not also metrizable.):

1. Every sequence in (X, <) has a subsequence that converges in (X, <).
2. Every monotone increasing sequence in X converges to a unique limit in X.
3. Every monotone decreasing sequence in X converges to a unique limit in X.
4. Every decreasing nested sequence of nonempty closed subsets S₁ ⊇ S₂ ⊇ ... in (X, <) has a nonempty intersection.
5. Every increasing nested sequence of proper open subsets S₁ ⊆ S₂ ⊆ ... in (X, <) fails to cover X.

Characterization by continuous functions

Let X be a topological space and C(X) the ring of real continuous functions on X. For each p ∈ X, the evaluation map ${\displaystyle \operatorname {ev} _{p}\colon C(X)\to \mathbb {R} }$ given by ev_p(f) = f(p) is a ring homomorphism. The

There are pseudocompact spaces that are not compact, though.

In general, for non-pseudocompact spaces there are always maximal ideals m in C(X) such that the residue field C(X)/m is a (

monad

of x₀).

Hyperreal definition

A space X is compact if its

ultrapower construction

) has the property that every point of *X is infinitely close to some point of X ⊂ *X. For example, an open real interval X = (0, 1) is not compact because its hyperreal extension *(0,1) contains infinitesimals, which are infinitely close to 0, which is not a point of X.

Sufficient conditions

• A closed subset of a compact space is compact.[18]
• A finite union of compact sets is compact.
• A
  continuous image of a compact space is compact.^[19]
• The intersection of any non-empty collection of compact subsets of a Hausdorff space is compact (and closed);
  • If X is not Hausdorff then the intersection of two compact subsets may fail to be compact (see footnote for example).[a]
• The product of any collection of compact spaces is compact. (This is Tychonoff's theorem, which is equivalent to the axiom of choice.)
• In a
  sequentially compact (assuming countable choice
  )
• A finite set endowed with any topology is compact.

Properties of compact spaces

• A compact subset of a Hausdorff space X is closed.
  • If X is not Hausdorff then a compact subset of X may fail to be a closed subset of X (see footnote for example).^[b]
  • If X is not Hausdorff then the closure of a compact set may fail to be compact (see footnote for example).^[c]
• In any
  complete
  . However, every non-Hausdorff TVS contains compact (and thus complete) subsets that are not closed.
• If A and B are disjoint compact subsets of a Hausdorff space X, then there exist disjoint open sets U and V in X such that A ⊆ U and B ⊆ V.
• A continuous bijection from a compact space into a Hausdorff space is a homeomorphism.
• A compact Hausdorff space is normal and regular.
• If a space X is compact and Hausdorff, then no finer topology on X is compact and no coarser topology on X is Hausdorff.
• If a subset of a metric space (X, d) is compact then it is d-bounded.

Functions and compact spaces

Since a

(Slightly more generally, this is true for an upper semicontinuous function.) As a sort of converse to the above statements, the pre-image of a compact space under a proper map is compact.

Compactifications

Every topological space X is an open

. By the same construction, every

locally compact

Hausdorff space X is an open dense subspace of a compact Hausdorff space having at most one point more than X.

Ordered compact spaces

A nonempty compact subset of the real numbers has a greatest element and a least element.

Let X be a simply ordered set endowed with the order topology. Then X is compact if and only if X is a complete lattice (i.e. all subsets have suprema and infima).^[21]

Examples

• Any finite topological space, including the empty set, is compact. More generally, any space with a finite topology (only finitely many open sets) is compact; this includes in particular the trivial topology.
• Any space carrying the
  cofinite topology
  is compact.
• Any
  Alexandroff one-point compactification
  . The one-point compactification of ${\displaystyle \mathbb {R} }$ is homeomorphic to the circle S¹; the one-point compactification of ${\displaystyle \mathbb {R} ^{2}}$ is homeomorphic to the sphere S². Using the one-point compactification, one can also easily construct compact spaces which are not Hausdorff, by starting with a non-Hausdorff space.
• The
  totally ordered set is compact. In particular, Sierpiński space
  is compact.
• No discrete space with an infinite number of points is compact. The collection of all singletons of the space is an open cover which admits no finite subcover. Finite discrete spaces are compact.
• In ${\displaystyle \mathbb {R} }$ carrying the lower limit topology, no uncountable set is compact.
• In the
  locally compact but is still Lindelöf
  .
• The closed
  open cover
  ${\textstyle \left({\frac {1}{n}},1-{\frac {1}{n}}\right)}$ for n = 3, 4, ...  does not have a finite subcover. Similarly, the set of
  rational numbers
  in the closed interval [0,1] is not compact: the sets of rational numbers in the intervals ${\textstyle \left[0,{\frac {1}{\pi }}-{\frac {1}{n}}\right]{\text{ and }}\left[{\frac {1}{\pi }}+{\frac {1}{n}},1\right]}$ cover all the rationals in [0, 1] for n = 4, 5, ...  but this cover does not have a finite subcover. Here, the sets are open in the subspace topology even though they are not open as subsets of ${\displaystyle \mathbb {R} }$.
• The set ${\displaystyle \mathbb {R} }$ of all real numbers is not compact as there is a cover of open intervals that does not have a finite subcover. For example, intervals (n − 1, n + 1) , where n takes all integer values in Z, cover ${\displaystyle \mathbb {R} }$ but there is no finite subcover.
• On the other hand, the extended real number line carrying the analogous topology is compact; note that the cover described above would never reach the points at infinity and thus would not cover the extended real line. In fact, the set has the homeomorphism to [−1, 1] of mapping each infinity to its corresponding unit and every real number to its sign multiplied by the unique number in the positive part of interval that results in its absolute value when divided by one minus itself, and since homeomorphisms preserve covers, the Heine-Borel property can be inferred.
• For every
  closed unit ball
  is compact.
• On the other hand, the closed unit ball of the dual of a normed space is compact for the weak-* topology. (
  Alaoglu's theorem
  )
• The Cantor set is compact. In fact, every compact metric space is a continuous image of the Cantor set.
• Consider the set K of all functions f : ${\displaystyle \mathbb {R} }$ → [0, 1] from the real number line to the closed unit interval, and define a topology on K so that a sequence ${\displaystyle \{f_{n}\}}$ in K converges towards f ∈ K if and only if ${\displaystyle \{f_{n}(x)\}}$ converges towards f(x) for all real numbers x. There is only one such topology; it is called the topology of
  Tychonoff theorem
  .
• A subset of the Banach space of real-valued continuous functions on a compact Hausdorff space is relatively compact if and only if it is equicontinuous and pointwise bounded (Arzelà–Ascoli theorem).
• Consider the set K of all functions f : [0, 1] → [0, 1] satisfying the
  Lipschitz condition |f(x) − f(y)| ≤ |x − y| for all x, y ∈ [0,1]. Consider on K the metric induced by the uniform distance
  ${\displaystyle d(f,g)=\sup _{x\in [0,1]}|f(x)-g(x)|.}$ Then by the Arzelà–Ascoli theorem the space K is compact.
• The
  bounded linear operator on a Banach space is a nonempty compact subset of the complex numbers
  ${\displaystyle \mathbb {C} }$. Conversely, any compact subset of ${\displaystyle \mathbb {C} }$ arises in this manner, as the spectrum of some bounded linear operator. For instance, a diagonal operator on the Hilbert space ${\displaystyle \ell ^{2}}$ may have any compact nonempty subset of ${\displaystyle \mathbb {C} }$ as spectrum.
• The space of Borel probability measures on a compact Hausdorff space is compact for the vague topology, by the Alaoglu theorem.
• A collection of probability measures on the Borel sets of Euclidean space is called tight if, for any positive epsilon, there exists a compact subset containing all but at most epsilon of the mass of each of the measures. Helly's theorem then asserts that a collection of probability measures is relatively compact for the vague topology if and only if it is tight.

Algebraic examples

• Topological groups such as an orthogonal group are compact, while groups such as a general linear group are not.
• Since the
  homeomorphic
  to the Cantor set, they form a compact set.
• Any global field K is a discrete additive subgroup of its adele ring, and the quotient space is compact. This was used in John Tate's thesis to allow harmonic analysis to be used in number theory.
• The spectrum of any commutative ring with the Zariski topology (that is, the set of all prime ideals) is compact, but never Hausdorff (except in trivial cases). In algebraic geometry, such topological spaces are examples of quasi-compact schemes, "quasi" referring to the non-Hausdorff nature of the topology.
• The spectrum of a
  Stone representation theorem. Stone spaces, compact totally disconnected Hausdorff spaces, form the abstract framework in which these spectra are studied. Such spaces are also useful in the study of profinite groups
  .
• The
  structure space of a commutative unital Banach algebra
  is a compact Hausdorff space.
• The Hilbert cube is compact, again a consequence of Tychonoff's theorem.
• A profinite group (e.g. Galois group) is compact.

See also

Notes

References

Bibliography

• Alexandrov, Pavel; Urysohn, Pavel (1929). "Mémoire sur les espaces topologiques compacts". Koninklijke Nederlandse Akademie van Wetenschappen te Amsterdam, Proceedings of the Section of Mathematical Sciences. 14.
• Arkhangel'skii, A.V.; Fedorchuk, V.V. (1990). "The basic concepts and constructions of general topology". In Arkhangel'skii, A.V.; Pontrjagin, L.S. (eds.). General Topology I. Encyclopedia of the Mathematical Sciences. Vol. 17. Springer.
  ISBN 978-0-387-18178-3
  ..
• Arkhangel'skii, A.V. (2001) [1994], "Compact space", Encyclopedia of Mathematics, EMS Press.
• Bolzano, Bernard (1817). Rein analytischer Beweis des Lehrsatzes, dass zwischen je zwey Werthen, die ein entgegengesetzes Resultat gewähren, wenigstens eine reele Wurzel der Gleichung liege. Wilhelm Engelmann. (Purely analytic proof of the theorem that between any two values which give results of opposite sign, there lies at least one real root of the equation).
• JFM 26.0429.03
  .
• Bourbaki, Nicolas (2007). Topologie générale. Chapitres 1 à 4. Berlin: Springer.
  ISBN 978-3-540-33982-3
  .
• MR 0124178
  .
• ISBN 978-0-471-54397-8
  .
• Arzelà, Cesare (1895). "Sulle funzioni di linee". Mem. Accad. Sci. Ist. Bologna Cl. Sci. Fis. Mat. 5 (5): 55–74.
• Arzelà, Cesare (1882–1883). "Un'osservazione intorno alle serie di funzioni". Rend. Dell' Accad. R. Delle Sci. dell'Istituto di Bologna: 142–159.
• Ascoli, G. (1883–1884). "Le curve limiti di una varietà data di curve". Atti della R. Accad. Dei Lincei Memorie della Cl. Sci. Fis. Mat. Nat. 18 (3): 521–586.
• S2CID 123251660
  .
• Gillman, Leonard; Jerison, Meyer (1976). Rings of continuous functions. Springer-Verlag.
• OL 1272666M
  .
• Kelley, John (1955). General topology. Graduate Texts in Mathematics. Vol. 27. Springer-Verlag.
• ISBN 978-0-19-506136-9
  .
• Lebesgue, Henri (1904). Leçons sur l'intégration et la recherche des fonctions primitives. Gauthier-Villars.
• Mack, John (1967). "Directed covers and paracompact spaces". Canadian Journal of Mathematics. 19: 649–654.
  MR 0211382
  .
• MR 0205854
  .
• Scarborough, C.T.; Stone, A.H. (1966). "Products of nearly compact spaces" (PDF). Transactions of the American Mathematical Society. 124 (1): 131–147.
  JSTOR 1994440. Archived
  (PDF) from the original on 2017-08-16..
• MR 0507446
  .
• Willard, Stephen (1970). General Topology. Dover publications.
  ISBN 0-486-43479-6
  .

External links

• Sundström, Manya Raman (2010). "A pedagogical history of compactness".
  arXiv:1006.4131v1 [math.HO
  ].

---

This article incorporates material from Examples of compact spaces on

Creative Commons Attribution/Share-Alike License

.