Netto's theorem

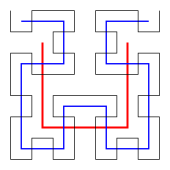
In

smooth manifolds preserve dimension. That is, there does not exist a continuous bijection between two smooth manifolds of different dimension. It is named after Eugen Netto.^[1]

The case for maps from a higher-dimensional manifold to a one-dimensional manifold was proven by

real line. Both Netto in 1878, and Georg Cantor in 1879, gave faulty proofs of the general theorem. The faults were later recognized and corrected.^[2]

An important special case of this theorem concerns the non-existence of continuous bijections from one-dimensional spaces, such as the

real line or unit interval, to two-dimensional spaces, such as the Euclidean plane or unit square

. The conditions of the theorem can be relaxed in different ways to obtain interesting classes of functions from one-dimensional spaces to two-dimensional spaces:

Space-filling curves are surjective continuous functions from one-dimensional spaces to two-dimensional spaces. They cover every point of the plane, or of a unit square, by the image of a line or unit interval. Examples include the Peano curve and Hilbert curve. Neither of these examples has any self-crossings, but by Netto's theorem there are many points of the square that are covered multiple times by these curves.^[1]
Jordan curves in the plane. However, by Netto's theorem, they cannot cover the entire plane, unit square, or any other two-dimensional region.^[1]

If one relaxes the requirement of continuity, then all smooth manifolds of bounded dimension have equal
Cartesian coordinates of points in the square. The ambiguities of decimal, exemplified by the two decimal representations of 1 = 0.999..., cause this to be an injection rather than a bijection, but this issue can be repaired by using the Schröder–Bernstein theorem.^[3]

References

^
MR 1299533. For the statement of the theorem, and historical background, see Theorem 1.3, p. 6. For its proof for the case of bijections between the unit interval
and a two-dimensional set, see Section 6.4, "Proof of Netto's Theorem", pp. 97–98. For the application of Netto's theorem to self-intersections of space-filling curves, and for Osgood curves, see Chapter 8, "Jordan Curves of Positive Lebesgue Measure", pp. 131–143.

^
MR 0476319

^
MR 2800330

[sagan-1] 
MR 1299533. For the statement of the theorem, and historical background, see Theorem 1.3, p. 6. For its proof for the case of bijections between the unit interval
and a two-dimensional set, see Section 6.4, "Proof of Netto's Theorem", pp. 97–98. For the application of Netto's theorem to self-intersections of space-filling curves, and for Osgood curves, see Chapter 8, "Jordan Curves of Positive Lebesgue Measure", pp. 131–143.

[dauben-2] 
MR 0476319

[gouvea-3] 
MR 2800330

[1]

[2]

[3]