Nine-point circle

circumcenter)

Nine-point circle (centered at the nine-point center

Note that the construction still works even if the orthocenter and circumcenter fall outside of the triangle.

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:

The midpoint of each side of the triangle
The foot of each altitude
The midpoint of the
orthocenter (where the three altitudes meet; these line segments lie on their respective altitudes).^[1]^[2]

The nine-point circle is also known as Feuerbach's circle (after Karl Wilhelm Feuerbach), Euler's circle (after Leonhard Euler), Terquem's circle (after Olry Terquem), the six-points circle, the twelve-points circle, the $n$ -point circle, the medioscribed circle, the mid circle or the circum-midcircle. Its center is the nine-point center of the triangle.^[3]^[4]

Nine significant points

The diagram above shows the nine significant points of the nine-point circle. Points $D, E, F$ are the midpoints of the three sides of the triangle. Points $G, H, I$ are the feet of the altitudes of the triangle. Points $J, K, L$ are the midpoints of the line segments between each altitude's vertex intersection (points $A, B, C$ ) and the triangle's orthocenter (point $S$ ).

For an

obtuse triangle

two of the altitudes have feet outside the triangle, but these feet still belong to the nine-point circle.

Discovery

Although he is credited for its discovery,

Charles Brianchon and Jean-Victor Poncelet had stated and proven the same theorem.) But soon after Feuerbach, mathematician Olry Terquem

himself proved the existence of the circle. He was the first to recognize the added significance of the three midpoints between the triangle's vertices and the orthocenter. (See Fig. 1, points

J, K, L

.) Thus, Terquem was the first to use the name nine-point circle.

Tangent circles

The nine-point circle is tangent to the incircle and excircles

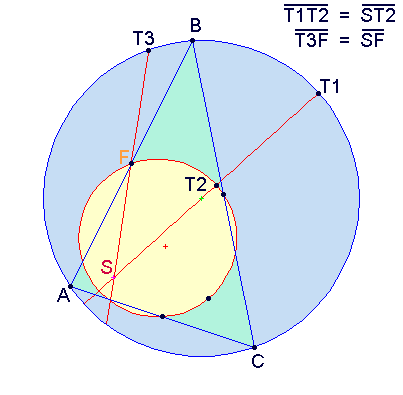
In 1822 Karl Feuerbach discovered that any triangle's nine-point circle is externally

Feuerbach's theorem. He proved that:

... the circle which passes through the feet of the altitudes of a triangle is tangent to all four circles which in turn are tangent to the three sides of the triangle…

^[5]

The triangle center at which the incircle and the nine-point circle touch is called the Feuerbach point.

Other properties of the nine-point circle

The radius of a triangle's circumcircle is twice the radius of that triangle's nine-point circle.^[6]^: p.153

Figure 3

A nine-point circle bisects a line segment going from the corresponding triangle's orthocenter to any point on its circumcircle.

Figure 4

The center $N$ of the nine-point circle bisects a segment from the orthocenter $H$ to the circumcenter $O$ (making the orthocenter a center of dilation to both circles):^[6]^: p.152

{\overline {ON}}={\overline {NH}}.

The nine-point center $N$ is one-fourth of the way along the Euler line from the centroid $G$ to the orthocenter $H$ :^[6]^: p.153

{\overline {HN}}=3{\overline {NG}}.

Let $ω$ be the nine-point circle of the diagonal triangle of a cyclic quadrilateral. The point of intersection of the bimedians of the cyclic quadrilateral belongs to the nine-point circle.^[7]^[8]

The nine-point circle of a reference triangle is the circumcircle of both the reference triangle's
orthic triangle (with vertices at the feet of the reference triangle's altitudes).^[6]
^: p.153

The center of all
rectangular hyperbolas that pass through the vertices of a triangle lies on its nine-point circle. Examples include the well-known rectangular hyperbolas of Keipert, Jeřábek
and Feuerbach. This fact is known as the Feuerbach conic theorem.

If an orthocentric system of four points $A, B, C, H$ is given, then the four triangles formed by any combination of three distinct points of that system all share the same nine-point circle. This is a consequence of symmetry: the sides of one triangle adjacent to a vertex that is an orthocenter to another triangle are segments from that second triangle. A third midpoint lies on their common side. (The same 'midpoints' defining separate nine-point circles, those circles must be concurrent.)
Consequently, these four triangles have circumcircles with identical radii. Let $N$ represent the common nine-point center and $P$ be an arbitrary point in the plane of the orthocentric system. Then

{\overline {NA}}^{2}+{\overline {NB}}^{2}+{\overline {NC}}^{2}+{\overline {NH}}^{2}=3R^{2}

where

R

is the common

circumradius

; and if

{\overline {PA}}^{2}+{\overline {PB}}^{2}+{\overline {PC}}^{2}+{\overline {PH}}^{2}=K^{2},

where

K

is kept constant, then the locus of

P

is a circle centered at

N

with a radius

{\tfrac {1}{2}}{\sqrt {K^{2}-3R^{2}}}.

As

P

approaches

N

the locus of

P

for the corresponding constant

K

, collapses onto

N

the nine-point center. Furthermore the nine-point circle is the locus of

P

such that

{\overline {PA}}^{2}+{\overline {PB}}^{2}+{\overline {PC}}^{2}+{\overline {PH}}^{2}=4R^{2}.

The centers of the incircle and excircles of a triangle form an orthocentric system. The nine-point circle created for that orthocentric system is the circumcircle of the original triangle. The feet of the altitudes in the orthocentric system are the vertices of the original triangle.
If four arbitrary points $A, B, C, D$ are given that do not form an orthocentric system, then the nine-point circles of $△ ABC, △ BCD, △ CDA, △ DAB$ concur at a point, the
circumconic
, centered at the common intersection point of the four nine-point circles, that passes through the four original arbitrary points as well as the orthocenters of the four triangles.
If four points $A, B, C, D$ are given that form a
homothetic
to the reference cyclic quadrilateral $ABCD$ by a factor of –½ and its homothetic center $N$ lies on the line connecting the circumcenter $O$ to the anticenter $M$ where

{\overline {ON}}=2{\overline {NM}}.

The orthopole of lines passing through the circumcenter lie on the nine-point circle.
A triangle's circumcircle, its nine-point circle, its
coaxal.^[10]

Kiepert hyperbola

are

{\frac {(b^{2}-c^{2})^{2}}{a}}:{\frac {(c^{2}-a^{2})^{2}}{b}}:{\frac {(a^{2}-b^{2})^{2}}{c}}

Trilinear coordinates for the center of the Jeřábek hyperbola are

\cos(A)\sin ^{2}(B-C):\cos(B)\sin ^{2}(C-A):\cos(C)\sin ^{2}(A-B)

Letting $x : y : z$ be a variable point in trilinear coordinates, an equation for the nine-point circle is

x^{2}\sin 2A+y^{2}\sin 2B+z^{2}\sin 2C-2(yz\sin A+zx\sin B+xy\sin C)=0.

Generalization

The circle is an instance of a

vertical angles with the triangle, but a nine-point hyperbola

occurs when

P

is in one of the three adjacent regions, and the hyperbola is rectangular when P lies on the circumcircle of

△ ABC

.

Notes

^ Altshiller-Court (1925, pp. 103–110)
^ Kay (1969, pp. 18, 245)
Lester R. Ford Award
) give a proof of the Nine-Point Circle Theorem.

^ Casey, John (1886). Nine-Point Circle Theorem, in A Sequel to the First Six Books of Euclid (4th ed.). London: Longmans, Green, & Co. p. 58.

^ Feuerbach & Buzengeiger 1822.

^ ^a ^b ^c ^d Posamentier, Alfred S., and Lehmann, Ingmar. The Secrets of Triangles, Prometheus Books, 2012.

S2CID 213935239
.

^ Fraivert, David (2018). "New applications of method of complex numbers in the geometry of cyclic quadrilaterals" (PDF). International Journal of Geometry. 7 (1): 5–16.

^ Altshiller-Court (1925, p. 98)

^ Altshiller-Court (1925, p. 241)

References

Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York:
LCCN 52013504

Feuerbach, Karl Wilhelm; Buzengeiger, Carl Heribert Ignatz (1822), Eigenschaften einiger merkwürdigen Punkte des geradlinigen Dreiecks und mehrerer durch sie bestimmten Linien und Figuren. Eine analytisch-trigonometrische Abhandlung (Monograph ed.), Nürnberg: Wiessner.

Kay, David C. (1969), College Geometry, New York:
LCCN 69012075

Fraivert, David (2019), "New points that belong to the nine-point circle", S2CID 213935239

Fraivert, David (2018), "New applications of method of complex numbers in the geometry of cyclic quadrilaterals" (PDF), International Journal of Geometry, 7 (1): 5–16

External links

"A Javascript demonstration of the nine point circle" at rykap.com

Encyclopedia of Triangles Centers by Clark Kimberling. The nine-point center is indexed as X(5), the Feuerbach point, as X(11), the center of the Kiepert hyperbola as X(115), and the center of the Jeřábek hyperbola as X(125).

History about the nine-point circle based on J.S. MacKay's article from 1892: History of the Nine Point Circle

Weisstein, Eric W. "Nine-Point Circle". MathWorld.

Weisstein, Eric W. "Orthopole". MathWorld.

Nine Point Circle in Java at
cut-the-knot

Feuerbach's Theorem: a Proof at
cut-the-knot

Special lines and circles in a triangle by Walter Fendt

Interactive Nine Point Circle applet from the Wolfram Demonstrations Project

Nine-point conic and Euler line generalization at Dynamic Geometry Sketches Generalizes nine-point circle to a nine-point conic with an associated generalization of the Euler line.

N J Wildberger. Chromogeometry. Discusses the nine-point circle with regard to three different quadratic forms (blue, red, green).

Stefan Götz, Franz Hofbauer: Ein einfacher Beweis für den Satz von Feuerbach mit koordinatenfreien Vektoren

[1] Altshiller-Court (1925, pp. 103–110)

[2] Kay (1969, pp. 18, 245)

[3] Lester R. Ford Award
) give a proof of the Nine-Point Circle Theorem.

[4] Casey, John (1886). Nine-Point Circle Theorem, in A Sequel to the First Six Books of Euclid (4th ed.). London: Longmans, Green, & Co. p. 58.

[FOOTNOTEFeuerbachBuzengeiger1822-5] Feuerbach & Buzengeiger 1822.

[PL-6] Posamentier, Alfred S., and Lehmann, Ingmar. The Secrets of Triangles, Prometheus Books, 2012.

[7] S2CID 213935239
.

[8] Fraivert, David (2018). "New applications of method of complex numbers in the geometry of cyclic quadrilaterals" (PDF). International Journal of Geometry. 7 (1): 5–16.

[9] Altshiller-Court (1925, p. 98)

[10] Altshiller-Court (1925, p. 241)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[10]

Nine significant points

Discovery

Tangent circles

Other properties of the nine-point circle

Generalization

See also

Notes

References

External links