Talk:Confidence interval/Archive 1

This page is an archive of past discussions. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page.

Having little background in stats, I was asked to give a 95% confidence interval for a physical measurement (of network latency). Reading this page almost killed me - fortunately, the teacher then explained that he just meant "remove the outermost 2.5% of the values (from both ends)". Assuming that this isn't actually wrong, something like that could be useful in the introduction.Anaholic (talk) 16:12, 21 November 2007 (UTC)

It's very very very wrong. A confidence interval need not include any of the values, let alone 97.5% of them. If he told you that that's what a confidence interval is, you should sue him for malpractice, or at least get the nearest professor of statistics to set him straight. Michael Hardy (talk) 02:34, 22 November 2007 (UTC)

Do you mean he told you to report the range of values in your data after removing the top 2.5% and the bottom 2.5% of these values? That might be sensible if you are doing some sort of simulation and each value is a summary of measurements, such as the mean of a bootstrap sample, but I suspect most of our readers will not be dealing with that sort of data. As general advice for any sort of data, it would be very wrong. -- Avenue (talk) 00:38, 22 November 2007 (UTC)

What he told us, /exactly/, was to find the min and max values in the result-set, reduce the distance between them by 5% (symmetrically), and use this as 2.5/97.5% confidence lines. Most of the values could indeed fall outside, though with these results - they don't. It's probably not very helpful to note that by his own admission he's not sure if this approach is /correct/, but it's what I've got. Also, when I said "physical measurement", I meant it - I actually threw some packets back and forth over wifi and measured the latency. I have no idea how this affects things. Anaholic (talk) 19:57, 24 November 2007 (UTC)

It's not even remotely similar to a correct way of getting a confidence interval. Michael Hardy (talk) 23:49, 24 November 2007 (UTC)

Michael Hardy is right. I'm a statastician and Anaholic is so far off base it's hard to imagine where he/she even learned this idea. If I had more time, I would rewrite this entire thing myself. But, until then, I hope a properly informed person takes charge of this. Thanks. Hubbardaie (talk) 02:51, 25 November 2007 (UTC)

Yes, Anaholic's teacher's algorithm won't produce anything like a confidence interval. I had begun to wonder if the issue was confusion between confidence intervals and tolerance intervals, but this method seems unlikely to give good tolerance intervals either. -- Avenue (talk) 13:23, 25 November 2007 (UTC)

As an aside, a formula for the confidence level of a tolerance interval running from the sample minimum to its maximum (without the 5% shrinkage) is given here (on page 7). This assumes the data is normally distributed. -- Avenue (talk) 14:02, 25 November 2007 (UTC)

I noticed that none of the discussion here asked what quantity the "confidence interval" was meant to be a confidence interval for. If it is meant to be a confidence interval for the "next observation" then the initial description of what to do may well be reasonable, although the later variant described by Anaholic seems to have no real basis. Melcombe (talk) 12:24, 19 February 2008 (UTC)

It would be great if someone could provide typical Z-values for 90%, 95% and 99% confidence intervals. 128.12.20.32 20:09, 11 February 2006 (UTC)

I just added a small section to the article about using Z-scores and a small table with common values. It's not well done, but at least it's something. I'm not sure that this article is the absolute best place to have put that data, but since it's what I came here for as well, I figure other people besides just the two of us would probably find it helpful. -- Zawersh 22:22, 17 May 2006 (UTC)

Could someone explain this:

"[the] frequentist interpretation which might be expressed as: "If the population parameter in fact lies within the confidence interval, then the probability that the estimator either will be the estimate actually observed, or will be closer to the parameter, is less than or equal to 90%""

I have a hard time figuring out how to write or deduce this in an actual mathematical formulation. It would help having the formulation of the claim, precisely stating what variables are used to denote random variables, and which identifiers are used as realizations of the random variables, and maybe the demonstration too (such as where the inequality come from? (Markov's etc))

A considerable part of this page is devoted to explaining what a confidence interval is not. I think this is appropriate, given how often the confidence intervals of classical statistics are misunderstood. However, I don't agree that the statement "There is only one planet Neptune" has any force. A person may say "Suppose that when Nature created the planet Neptune, this process selected a weight for the planet from a uniform distribution from ... to ....". This, of course, is a Bayesian approach.

No, it's not! That is a frequentist parody of the Bayesian approach! The Bayesian approach is to regard probabilities as degrees of belief (whether logically determined or subjective) in uncertain propositions. (Bayesians have generally done a lousy job of defending themselves against the above attack, though. In one notable case, Jim Berger, now of Duke University, I think, it is simply because he doesn't really care about the issue involved. (I realize that the statement above that I called an "attack" probably wasn't intended to be an attack, but it almost may as well have been.)) Michael Hardy 00:27, 21 Dec 2004 (UTC)

If the fact that "There is only one planet Neptune" had any such implications, then the Bayesian approach would be rendered invalid.

Absolutely wrong. For the reason I gave above. The fact that there is only one planet Neptune does not invalidate Bayesianism precisely because Bayesianism assigns probabilities to uncertain propoisitions, not to random events. Michael Hardy 00:27, 21 Dec 2004 (UTC)

I don't think this is what the author of the page intended.

I'm the author and I'm a Bayesian. Deal with it. You have simply misunderstood. Michael Hardy 00:27, 21 Dec 2004 (UTC)

The difference between the Bayesian approach and the classical approach is not that they obtain different answers to the same mathematical problem. It is that they set up different mathematical problems for the same practical problem. The Bayesian approach allows creating a stochashic model for the process that picks a value that may have been selected in the past.

No. "In the past" misses the point completely. Michael Hardy 00:27, 21 Dec 2004 (UTC)

Classical statistics does not allow creating such a model for certain parameters that are already realized. (However it does allow probability models for things like sample means, which may, in fact, have been already realized by the time the statistician is reading about a given classical approach.)

I think there are two better ways to convey why the usual misinterpretation of classical confidence intervals is wrong. First we may appeal to the fact that "conditional probabilities" are different than "unconditional probabilitites". As an example of this, suppose we select a value of a random variable X from a normal distribution with fixed, but unknown, mean M and fixed, but unknown standard deviation Sigma. What is the probability that X is equal or greater than M. The answer is 0.5.

What is the conditional probability that X is equal or greater than M given that X > 100.0. We can no longer give an answer. We can't even say that the probability is greater than 0.5. That would false if M happens to be -10.0, for example. What is the probability that X is equal or greater than M given that X = 103.2? We cannot give a numerical answer for this conditional probability either.

This impass is because of the mathematical formulation used. If we had set it up so that there was a prior distribution of the mean then we might find an answer, or at least say that an answer, different than 0 or 1, exists. As problem is stated, we can only say that above probabilities have unknown values and their value is either 0 or 1.

People find it counter intuitive that finding an answer to one question is possible and then, being given more information, it becomes impossible to answer it. This is the paradoxical sensation that conditional probabilities produce. Confidence intervals are just one example.

A second way of explaining the misinterpretation is the phrase "The reliability of a reporting process is different that the reliability of a specific report". The "confidence" of classical confidence intervals is a number which describes the reliability of the sampling process with respect to producing intervals that span the True value of the parameter in question. This will be different than the "confidence" we can assign to a specific report, a numerical interval.

As a simple example: Suppose we have a non-necessarily fair coin. (Pretend it is bent and deformed.) A lab assistant takes the coin in to a different room and flips it. He write the actual result ("H" or "T") down on two slips of paper. Then he writes a False result down on one slip of paper. (So, if the coin lands heads, he creates two slips of paper which say "H" and one that says "T".) He picks a slip of paper at random and gives it to us.

What is the probability that the slip of paper we receive contains the correct result? The answer is 2/3. This is the reliability of the reporting process.

If the paper says "H", what is probability that the coin landed heads? The answer to this is no necessarily 2/3. This is a question about the reliability of a specific report. Let p be the probability that the coin landed heads. Then if p is small, the probability that the report is true is smaller than 2/3. This can be shown by computing the conditional probability. (I am sure that readers who refuse to accept the correct answer to the Monte-Hall problem can start a lively debate about this example too!)

If we refuse to admit a probability model for the coin being tossed then all we can say is that the report of "H" is either True or False. There is no probability of 2/3 about it. The probability that it is heads is unknown but either 0 or 1. People can object to such a statement by saying things like "If the weather person says there is a probability of 50% that it rains, it either rains or doesn't. This does not contradict the idea of probability." The reply to this is that the weatherperson, by giving a probability, has assumed that there is a probability model for the weather. Unless the statement of a mathematical problem admits such a model, no probability other than 0 or 1 can be assigned to its answer.

If we rewrite the above example so that the lab assistant is opening a sealed container which contains either Hydrogen or Thorium, then perhaps the non-probabilistic model comes to mind before the one that admits probability.

Another topic is whether an entry on "confidence intervals" should treat only frequentist confidence intervals, since is such a thing as a Bayesian confidence interval. The corrrect interpretation of a Bayesian confidence interval sounds like the misinterpretation of the frequentist confidence interval.

For example suppose the practical problem is to say what can be deduced from a random sample of the weights of 10 year old children if the mean is 90.0 and the standard deviation is 30? A typical frequentist approach is to assume the population is normally distributed with a standard deviation is also 30.0 and that the population mean is a fixed but unknown number. Then, ignoring the fact that we have a specific sample mean, we can calculate the "confidence" that the population mean is within, say, plus or minus 10 lbs of the sample mean produced by the sampling process.

But we can also take a Bayesian approach by assuming that the Natural process that produced the population picked the population mean at random from a uniform distribution from, say, 40 lbs to 140 lbs. One may then calculate the probability that the population mean is in 90-10 lbs to 90+10 lbs. This number is approximately the classical answer for "confidence". Only intervals outside or on the edge of the interval 40 to 140 lbs produce answers that differ significantly from frequentist “confidenceâ€. These calculations can be done with the same table of the Normal Distribution as frequentists use.

The fact that Bayesian confidence intervals on uniform priors often give the same numerical answers as the usual misinterpretation of frequentist confidence intervals is very interesting.

Actually, the problem is that Bayesian is often misunderstood to be purely subjective. While Bayesian allows for use of subjective probabilities in prior knowledge, there are also objective Bayesian calculations since prior knowledge can also be based on a previous non-Baysian sampling. I find this a mostly moot debate since a frequentist appraisal of Bayesian analysis would be consistent - that is, historically, a large number of separate Bayesian studies would be distributed exactly as the Bayesian calculation said it would. In other words, if the Bayesian analysis said p(X>A)=.8 in a large number of separate empirical studies, the strict frequentist would find that X>A about 80% of the time (90% of the time when the Bayesian says p(X>A)=.9, etc.). In effect, the frequentist would have to conclude that the Bayesian analysis was consistent with its own historical frequency distribution. This is why this debate is irrelevant to most real-world statisticians even while it seems to pre-occupy amateurs and first-year stats students. The phrase "confidence interval" is equally meaningful in both senses (which, as I stated, are really the same sense when the historical frequency of Bayesian analysis is considered) and, in fact, Bayesians are perfectly justified using it. If frequnentists must insist that historical frequencies alone are the only meaninful source of quantifying uncertainty, then perhaps they can present a frequentists theory of lingistics to explain why this phrase should be used only that way. Good luck with that. Hubbardaie 02:39, 9 November 2007 (UTC)

---

I have not yet read all of the anonymous comments above, but I will comment on a small part:

A person may say "Suppose that when Nature created the planet Neptune, this process selected a weight for the planet from a uniform distribution from ... to ....". This, of course, is a Bayesian approach.

That is wrong. That is not the Bayesian approach. Rather, it is a frequentist parody of the Bayesian approach. The mathematics may be identical to what is done in the Bayesian approach, but the Bayesian approach does not use the mathematics to model anything stochastic, but rather uses it to model uncertainty by interpreting probabilities as degrees of belief rather than as frequencies. Bayesianism is about degree-of-belief interpreations of mathematical probability. Michael Hardy 19:09, 7 Sep 2003 (UTC)

---

"But if probabilities are construed as degrees of belief rather than as relative frequencies of occurrence of random events, i.e., if we are Bayesians rather than frequentists, can we then say we are 90% sure that the mass is between 82 − 1.645 and 82 + 1.645? "

Well, yes, at least from what I got from the page that is what the confidence interval means. But the question is can we say that with probability 0.9 the mass is between 82 − 1.645 and 82 + 1.645? And the answer is clearly NO, because one measurement can give 82 and another can give 78. The intervals 82 − 1.645 and 82 + 1.645 and 78 − 1.645 and 78 + 1.645 don't overlap, so it's not possible to be in each one with probability 0.9. This is not a philosophical question, it's a question that the probability can't be more than 1.

I'm surprised that anyone is getting a clear "yes" as the answer to that question, from the content of this article. The second paragraph above is horribly horribly confused. It drops the context. The question was whether we can be 90% sure given a certain set of measurements that give that confidence interval, and no other relevant information (such as other measurements giving a different confidence interval). Michael Hardy 17:25, 17 June 2007 (UTC)

Sorry to be "new" here and probably poorly placed amongst all this philosophy. I read the whole "Bayesian / Frequentist" thing and went "huh?". Two questions ... Firstly, given knowledge of two estimations of the mass of Neptune as per the 78 vs 82 example just above, surely I would have to recalculate confidence intervals? ie given only a single attempt to measure the mass I CAN say I am 90% sure the mass is in 82 +/- 1.645. Secondly, isn't the point that while the mass may be (almost) fixed it's the error inherent in my measuring process that is random? So when I say the mass has 90% chance of being in 82 +/- 1.645 I'm obviously not saying the mass is variable I'm saying my measurement process is variable ... I'm saying I measure the mass at 82 and the error in that measurement has 90% chance of being less than 1.645 ... I don't understand why this could be philosophically objectionable to anyone. 203.132.83.185 14:38, 8 November 2007 (UTC) Joe

Isn't anyone who is willing to assume a prior distribution qualified to be a Bayesian?

Certainly not. A frequentist may use a prior distribution when the prior distribution admits a frequency interpretation. Michael Hardy 00:33, 21 Dec 2004 (UTC)

Must it be done with a particular interpretation in mind? Doesn't someone who assumes a probability model use subjective belief?

Not necessarily. Michael Hardy 00:33, 21 Dec 2004 (UTC)

Is saying that "I assume the following probability model for the process that created Neptune is ..." less or more subjective than saying "My subjective belief for the probability of the parameters of Neptune is given by the following distribution..."? The former might be a modest kind of Bayesian, but I think it is a good way to introduce prior distributions to a world that is perceives frequentist statistics to somehow be "objective" and Bayesian statistics to be "subjective".

Frequentist statistics is willing to assume a probability model for the sample parameters but unwilling to assume a probability model for the population parameters in the typical textbook examples of confidence intervals and hypothesis testing. But a frequentist analysis of something like "Did the crime rate in Detroit remain the same in 2002 as it was in 2001" will be analyzing (here in the year 2003) events (the "sample" realization of a number of crimes from some imagined distribution or distributions) that have already happened. The fact that something (the reported numbers of crimes) already has a True and realized value does not prevent a frequentist from computing probabilities since he has assumed a probabilistic model for the sample parameters. So I don't think the the fact that there is only one planet Neptune is a pro-frquentist or anti-frequentist fact. The mathematical interpretation of a given type of confidence interval depends on the mathematical problem that is stated. The same physical situation can be tackled in different ways depending on what mathematical model for it is picked. If I want to be a flaming Bayesian then I announce that my prior represents my subjective belief. But there are less blatant ways to be subjective. One of them is to say that I have assumed a simplified probability model for the creation of Neptune's parameters.

The only place where I see a difference in the modest Bayesian and the flaming Bayesian is in the use of "improper priors". These are "mathematical objects" which are not probability distributions but we compute with them as if they were. An not all flaming Bayesians would go for such a thing.

I didn't mean to be anonymous, by the way. I'm new to this Wikipedia business and since I was logged-in, I thought my name would be visible. Also, my thanks to whoever or whatever fixed up the formatting of the comments. I pasted them in the miserable little text window from a *.txt file created by Open Office and they looked weird but I assumed the author of the page might be the only one who read them and I assumed he could figure them out! I notice these comments which were diligently typed in the text window without accidental carriage returns also look wrong in the preview. The lines are too wide.

Stephen Tashiro

PS: I think some of your comments have considerable merit, even though you've horribly mangled the definition of Bayesianism. Michael Hardy 00:33, 21 Dec 2004 (UTC)

---

The legibility problem resulted from your indenting by several characters. When you do that, the text will not wrap. Michael Hardy 12:24, 9 Sep 2003 (EDT) PS: More later.... Michael Hardy 12:24, 9 Sep 2003 (EDT)

I think the issues in the article (and in my previous comments) would be clarified by distiguishing between the 1) The disagreements in how a statistical problem is posed as a mathematical problem and 2) The correct and incorrect interpretation of the solutions to the mathematical problems. If we assume the reader already is familiar with the different mathematical problems posed by Bayesian and Frequentist statistics then he may extract information about 2) from it. But a reader not familiar with any distinction in the way the problem is posed may get the impression that mathematical results have now become a matter of opinion. It seems to me that the Frequentists pose one problem: The parameter of the distribution is in a fixed but unknown location. What is the probability that the sampling process produces a sample parameter within delta of this location? The Bayesians pose another problem: There is a given distribution for the population parameter. Given the sample parameter from a specific sample, what is the probability that the population parameter is within delta of this location. The disagreements in interpretation involve different ways of posing a practical situation as a mathematical problem. They don't involve claims that the same well-posed mathematical problem had two different answers or does or does-not have a solution. If there are indeed Bayesians or Frequentists who say that they will accept the mathematical problem as posed by the other side but interpret the answer in a way not justified by the mathematics then this is worthy of note.

In this equation:

${\displaystyle S^{2}={\frac {1}{n-1}}\sum _{i=1}^{b}\left(X_{i}-{\overline {X}}\,\right)^{2}.}$

The term "b" isn't explained. I would've thought it should be "n"; we're taking the sum of the squares of the differences from the mean of all the members of the sample, and the sample has already been defined as X₁, ..., X_n. If this isn't a typo, would someone be able to explained it in the article? JamesMLane 07:48, 20 Dec 2004 (UTC)

Just a typographical error. I've fixed it. Michael Hardy 03:11, 21 Dec 2004 (UTC)

I'm not happy with the following...

...if we are Bayesians rather than frequentists, can we then say we are 90% sure that the mass is between 82 − 1.645 and 82 + 1.645? Many answers to this question have been proposed, and are philosophically controversial. The answer will not be a mathematical theorem, but a philosophical tenet.

It obscures that fact that Bayesians have good solution to this problem (namely, credible intervals) which

a) do not have a counter-intuitive interpretation

b) the calculated interval takes the information in the prior into account, so it's an interval estimate based on everything you know.

It is not clear why the author considers credible intervals (a mainstream Bayesian concept) to be philosophically controversial.Blaise 19:27, 1 Mar 2005 (UTC)

I wrote those words. They are NOT about Bayesian credible intervals; obviously they are about CONFIDENCE INTERVALS. Bayesian credible intervals are another matter. Michael Hardy 22:13, 1 Mar 2005 (UTC)

This distinction is not widely accepted as meaningful. Statisticians and decision science researchers routinely use "confidence interval" in the broad sense including subjective intervals. The frequentist use of the term is a mere subset of legitimate uses. It is simply an interval for a parameter with a stated probability of containing the true value. How that interval is computed is a separate issue and it is how we distinguish a subjective confidence interval from an estimate of a population parameter based purely on non-bayesian sampling. If anyone is going to continue to make this distinction then they should 1) offer specific sources (not original research) that it is an error to use the term in this broader sense and 2) start a section about this controversy because it is also clear that it is widely used by even specialists to for subjective assessments, non-subjective Bayesian methods, as well as sampling methods that ignore prior knowledge.Hubbardaie 16:24, 28 October 2007 (UTC)

Prosecutor's fallacy

The reference to

03:36, 14 May 2007 (UTC))

It is definitely incorrect for both. It is a complete misinterpretation of the prosecutor's fallacy. I removed it from here. Hubbardaie 16:25, 28 October 2007 (UTC)

In regard to the sentence in the article which states...

"Critics of frequentist methods suggest that this hides the real and, to the critics, incomprehensible frequentist interpretation which might be expressed as: "If the population parameter in fact lies within the confidence interval, then the probability that the estimator either will be the estimate actually observed, or will be closer to the parameter, is less than or equal to 90%".

...the statement is indeed incomprehensible but it is not a valid interpretation, frequentist or otherwise.

Speaking of incomprehnsible... isn't Wikipedia supposed to be accessible to all? I just opened up this article and was immediately turned off by the math-heavy first sentence. I am not being anti-intellectual - obviously, there is a (large) place for math (or symbols, etc.) in an article such as this. But I think a simple laymen's explanation ought to come first.

Many thousands of Wikipedia mathematics articles are comprehensible only to mathematicians, and I don't think that's a problem. This article is certainly comprehensible to a broader audience than mathematicians, but yes, in the case of this article, that could be made still broader. But it's not appropriate to insist we get rid of all the tens of thousands of math articles that cannot be made comprehensible to lay persons. Michael Hardy 23:15, 27 December 2005 (UTC)

To the parent, I concur wholeheartedly. To Micheal (with all due respect to your impressive Barnstar status), I disagree with your statement that certain subjects are (or should be) incomprehensible to lay people. All concepts (and therefore articles) can, and should, be made comprehensible to lay people to some degree. The degree to which they can be made comprehensible depends on the ability of the reader to comprehend. The degree to which they are made comprehensible depends on the the skill and intent of the author. In the case of an encyclopedia article, the onus falls on the author to ensure maximum possible comprehensibility to the widest possible audience. Wikipedia is a crucial medium of global eduction. Dhatfield 08:33, 12 November 2007 (UTC)

Re: Speaking of incompreincomprehnsible... I agree, lay persons cannot get a quick idea of math concepts at wikipedia, but they should be able to, and stating that opinion is not the same as "insist[ing] we get rid of all the tens of thousands of math articles that cannot be made comprehensible to lay persons." There should be a higher, more general discussion of the concept first, then you math geeks can duke it out regarding the nitty gritty stuff afterwards. Would someone mind writing a more general explanation of CI? Maybe for someone like me, who took intro statistics in Jr college but forgot most of it. Thanks

I am not sure concerning the so-called frequentist interpretation of the Neptun example. I would say that if I would have tried to determine the weight of the planet 100 times 95% of my intervals would contain the true weight. Accordingly, if I pick one of those 100 intervals randomly, my chances to get one covering the true weight are 95%. At least with my current understanding, I would interpret that as a 95% probability that the interval contains the parameter. What is wrong with that and what is the practical conclusion from a 95% credible interval? [email protected]

I wrote the following paragraph (starting with "I share Harry..." and after a few months I realized it is nonsense, and that the article is correct. Nevertheless I will maintain this paragraph so that readers who have the same illusions as me know that they are wrong. Nagi Nahas

I share Harry's opinion that the interpretation "If the population parameter in fact lies within the confidence interval, then the probability that the estimator either will be the estimate actually observed, or will be closer to the parameter, is less than or equal to 90%" is wrong. I do not want to modify it myself as I know that Michael is more knowledgeable in this field than I am , but I hope he will look into this. I think the following interpretation is correct: the 90% confidence interval is the set of all possible values of the actual parameter for which the probability that the estimator will be the estimate actually observed or a more extreme value will be 90% or more. I agree with Harry's interpretation : "I would say that if I would have tried to determine the weight of the planet 100 times 95% of my intervals would contain the true weight. " I have some reserves about the statement "At least with my current understanding, I would interpret that as a 95% probability that the interval contains the parameter." The reason of my objection is the ambiguity of the statement: It can refer to 2 different experiments: 1-you fix a certain value of the parameter, take several samples of the distribution and count how many times the true value of the parameter falls within the confidence interval. In that case Harry's interpretation is correct. 2-Same as 1) but using a different value of the parameter each time : That's totally wrong, because you'll then have to specify the probability distribution you're taking the parameter values from, and in that case you're doing Bayesian stuff. Nagi Nahas . Email: remove_the_underscores_nnahas_at_acm_dot_org.

I have normally distributed observations x_i, with i from 1 to N, with a known mean m and standard deviation s, and I would like to compute the upper and lower values of the confidence interval at a parameter p (typically 0.05 for 95% confidence intervals.) What are the formulas for the upper and lower bounds? --James S. 20:30, 21 February 2006 (UTC)

I found http://mathworld.wolfram.com/ConfidenceInterval.html but I don't like the integrals, and what is equation diamond? Apparently the inverse error function is required. Gnuplot has:

     inverf(x)         inverse error function of x

--James S. 22:00, 21 February 2006 (UTC)

The simplest answer is to get a good book on statistics, because they almost always have values for the common confidence intervals (you may have to look at the tables for Student's t-distribution in the row labelled n = infinity). Confusing Manifestation 03:57, 22 February 2006 (UTC)

The question was how to calculate, not how to look up in a table. --171.65.82.76 07:36, 22 February 2006 (UTC)

In which case the unfortunate answer is that you have to use the inverse error function, which is not calculable in terms of elementary functions. Thus, your choices are to look up a table, use an inbuilt function, or use the behaviour of erf to derive an approximation such as a Taylor series. (Incidentally, I think equation "diamond" is meant to be the last part of equation 5.) Confusing Manifestation 16:12, 22 February 2006 (UTC)

Any general statistical package worth its salt (including free ones such as

R) will let you calculate the inverse error function mentioned above for any p, as will most spreadsheets (e.g. see the NORMSINV function in MS Excel). -- Avenue

12:07, 23 February 2006 (UTC)

Perl5's Statistics::Distributions module has source code for

 $u=Statistics::Distributions::udistr (.05);
 print "u-crit (95th percentile = 0.05 sig_level) = $u\n";

... from which I posted a wrong solution. I should have been using:

sub _subuprob {
	my ($x) = @_;
	my $p = 0; # if ($absx > 100)
	my $absx = abs($x);

	if ($absx < 1.9) {
		$p = (1 +
	$absx * (.049867347
	+ $absx * (.0211410061
	+ $absx * (.0032776263
	+ $absx * (.0000380036
	+ $absx * (.0000488906
       + $absx * .000005383)))))) ** -16/2;
	} elsif ($absx <= 100) {
		for (my $i = 18; $i >= 1; $i--) {
			$p = $i / ($absx + $p);
		}
		$p = exp(-.5 * $absx * $absx) 
			/ sqrt(2 * PI) / ($absx + $p);
	}

	$p = 1 - $p if ($x<0);
	return $p;
}

Thanks in advance. --James S. 18:16, 25 February 2006 (UTC)

Would the use of critical values instead of the t-distribution be better here? --James S. 08:13, 27 February 2006 (UTC)

This article is not structured well for reference or orientation.

The text frequently and colloqially digresses into what the topic is NOT, which limits the reference/skim value (more seperation needed). It's not that the latter points aren't valid -- they are just not clearly nested within the context of what is ultimately a positive statement/definition/reference entry.

I feel like this article could be distilled by 15-20% with refactoring (ex: 2 sections after the intro... What CIs ARE, What CIs are NOT; clearer seperation of the negative points, emphasising bullets), and removal of the conversational tone that adds unessential bulk.

I am not an expert in this field and do not feel qualified to make these mods. —Preceding unsigned comment added by 205.250.242.67 (talk • contribs) 11 June 2006

This whole article appears to blur the distinction between a (frequentist) confidence interval and a (Bayesian) credible interval. Eg, right at the start, it claims that a confidence interval is an interval that we have confidence that the parameter is in, and then again in the practical example "There is a whole interval around the observed value 250.2 of the sample mean with estimates one also has confidence in, e.g. from which one is quite sure the parameter is in the interval, but not absolutely sure...Such an interval is called a confidence interval for the parameter". This is surely wrong. Anyone care to defend it?Jdannan 05:28, 6 July 2006 (UTC)

OK, no-one replied, so I've had a go at clarifying the confidence/credible thing. Please feel free to improve it further.Jdannan 06:54, 10 July 2006 (UTC)

The statement near the beginning, "In modern applied practice, almost all confidence intervals are stated at the 95% level" needs a citation. Although 95% CIs are common, especially in text books and in certain fields, 95% is certainly not the most common level of confidence in all fields, especially in some engineering fields. There is really no reason for this statement, especially in the introduction. Perhaps a seperate section could be added in the body that discusses what levels of confidence are commonly used in various fields. —The preceding

) .

I think the statement is both wrong and unhelpful so near the beginning. Melcombe (talk) 12:12, 19 February 2008 (UTC)

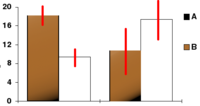
I've removed this chart from the article. I feel the caption is misleading, because the implication is that you can tell directly from the diagram whether the differences on the right are statistically significant or not. But you can't; this depends instead on whether the confidence interval for the difference includes zero. (If the comparison was for two independent groups of equal sizes with equal variances, then the confidence interval for the difference would be roughly 1.4 times larger than the confidence interval for each group. Judging by eye, any difference here would then be only marginally significant.)

I think the diagram could lead readers to believe that overlapping confidence intervals imply that the difference is not significant, which seems to be a common fallacy. -- Avenue 03:47, 3 August 2006 (UTC)

Actually, that's the truth. 75.35.79.57 04:30, 19 June 2007 (UTC)

No, it's not, because the standard error for a difference is not the sum of the individual standard errors. (Variances sum, assuming independence, but standard errors don't.) I'll see if I can track down a source, to avoid any further confusion. I've left the diagram in the article for now, but I think even the new caption is potentially misleading. People will tend to assume the converse of what is stated there now. -- Avenue 07:55, 19 June 2007 (UTC)

Avenue is correct. The Journal of the Royal Statistical Society should suffice. "It is a common statistical misconception to suppose that two quantities whose 95% confidence intervals just fail to overlap are significantly different"[1]. --Limegreen 23:41, 3 July 2007 (UTC)

That's "just" true, as there isn't much room for the disjoint intervals before the difference becomes significant. Is there any dissent that when the intervals do overlap that the difference is not significant? ←

Ben^B4

08:52, 4 September 2007 (UTC)

Absolutely there is dissent. I don't think anyone would dissent that where the CIs don't overlap there is a significant difference, but CIs can overlap by a large margin. There is a nice example here (see Fig 2 [2]). I'm really just re-hashing the authors argument, but while there are valid arguments for using CIs where the actual population value is of interest, it's next to useless if you want to know if there is a difference. As an aside, it would be much more appropriate to display a standard error on a graph. Adding 2 SEs together is more likely to approximate 2 x the pooled SE, which would indicated a significant difference. The linked paper suggests that a "by eye" test might be better done with 1.5 x SE error bars, but that is still rather less than the CI. --Limegreen 10:57, 4 September 2007 (UTC)

My neighbor is working on her thesis (for her PhD, iiuc) and she mentioned that she needed to (I forget exactly how she phrased it), but essentially she had to figure out how many times she had to run an (her) experiment to determine that it had something like a 95% confidence level of being correct.

(Actually, the conversation occurred about a year ago.) I finally thought of checking Wikipedia to see if the calculation was here or was linked from here. If it is here, I don't recognize it. I'm guessing (hoping?) that it is a fairly simple calculation, although maybe you have to make some assumptions about the (shape of the probability) distributions or similar.

Can anyone point to a short article which explains how to do that, along with the appropriate caveats (or pointers to the caveats). (I'm assuming that by now she has solved her problem, but I am still curious--I thought that 35 years or so ago I had made a calculation like that in the Probability and Statistics course I took, but couldn't readily find it when re-reviewing the textbook.)

Rhkramer 16:01, 3 September 2006 (UTC)

Maybe your neighbor wanted to know how many observations are needed to get a confidence interval no longer than a specified length? Or maybe what she was concerned with was

hypothesis testing? Anyway, it probably is a pretty routine thing found in numerous textbooks, but your question isn't very precisely stated. Michael Hardy

01:51, 4 September 2006 (UTC)

Formula used in the definition of a CI

In the article, ${\displaystyle \Pr(U<\theta <V|\theta )=x}$ is used to define a CI. But what is ${\displaystyle \theta }$ in this? Formally, the thing behind the bar (|) must be an event, but what event is "${\displaystyle \theta }$"? Would be glad to receive some clarifications. hbf 22:35, 6 December 2006 (UTC)

No, it's not necessary for the thing behind the bar to be an event. Certainly the concept of conditioning in probability as usually first presented to students does require that. But there are more general concepts. One can condition on the value of a random variable and get another random variable. And one can even condition on the value of a paramter that indexes a family of probability distributions. That's what's being done here. Statisticians do this every day; probabilists less often. Michael Hardy 23:57, 6 December 2006 (UTC)

I also don't understand this part of the article, and your comment also does not clarify what the meaning of ${\displaystyle \theta }$ is in this respect. —The preceding

unsigned comment was added by 219.202.134.161 (talk

) 15:56, 24 January 2007 (UTC).

I'll read it as "the probability that θ lies between U and V, for this particular value of θ". A better way to put it might be ${\displaystyle \Pr(U<\theta <V|\theta =\theta ^{*})}$, where θ denotes the unknown parameter and ${\displaystyle \theta ^{*}}$ is a concrete value we hypothesize for it (e.g. 1.234). Bi 04:17, 7 February 2007 (UTC)

Write it this way: ${\displaystyle \mathrm {P} _{\theta }(\{U<\theta <V\})}$, where P_θ is the distribution involved with the parameter θ.Nijdam 21:39, 4 July 2007 (UTC)

The notation is certainly wrong and the article as it stands is unhelpful in placing too much emphasis on the notion that the quantity the confidence interval relates to must be a fixed one. Important applications where this is not the case arise in regression analysis. See for example Draper and Smiths "Applied Regression Analysis", Section 3.1, which deals with confidence intervals for not only the location of the regression line (for a given "x"), but also with confidence intervals for both a single new independent outcome at a given x, and for the sampe mean of a set of new observations at a given x. In these cases, treated entirely within the frequentist point of view, the target quantity is random. ... and inspecting the theory shows that, in the coverage probability of the interval, the randomness of the target is treated by marginalising over this randomness rather than conditioning on the random outcome. Melcombe (talk) 12:55, 19 February 2008 (UTC)

Their (frequentist) methodology addresses some interesting problems/mistakes people make when using confidence intervals, and is widely used in high-energy physics which is one of the most statistics-heavy branches of science.

Aharel 23:21, 31 July 2007 (UTC)

I am a physician and a colleague of mine and I have been debating this issue.

A clinical trial is released comparing one drug against another. A result for the benefit/harm of drug A compared to drug B is expressed in terms of an odds ratio. OR>1.0 signifies that drug A is better, OR<1.0 signifies that drug B is better. The result is 1.2 (95% CI 0.8-1.6). I dismiss on the basis of this result that there is any meaningful difference between the two drugs

My colleague however says that because the range 1.0-1.6 is larger than 0.8-1.0 then there is a greater probability that the true result lies in this range so a greater probability that drug A is better so he wants to use it. In the article it seems that probabilities cannot be deterimed from the CI only confidences. Is my colleague right to say the true value has a higher probability of being in the beneficial range? If not, is he correct to say that he has greater confidence that it is within the beneficial range? What in laymans terms (terms that I can explain to my medical students) is the difference between a confidence of 95% and a probability of 0.95?

Even if my colleague is right is this really justifiable statistically? Richard Shepherd (talk) 10:40, 18 January 2008 (UTC)

You are correct that there is no evidence that Drug A is better than Drug B. If your colleague's interpretation were correct, then you would see this sort of argument used all the time! Essentially your colleague is calculating a weaker confidence interval (probably about 65%). So rather than the accepted 1 in 20 chance, it's a 1 in 3 chance, which makes a false positive finding really quite likely. I'm slightly more convinced by my initial argument. If it was valid to do what your colleague suggests, everybody would be doing it. --Limegreen (talk) 11:26, 18 January 2008 (UTC)

I agree with both you and your colleague to some degree. The trial has not shown a

statistically significant

difference between the drugs, that's true, but there's a big jump from that fact to the conclusion that there is no meaningful difference. "Meaningful" seems to imply medical significance, and you haven't said whether an odds ratio of 1.2 would be meaningful in that sense. I imagine it could well be (while an odds ratio of 1.01 probably wouldn't be).

The best estimate of the odds ratio from the trial is 1.2, so if there is no other information, it's more likely than drug A is better than drug B than vice versa. Your colleague is right is that respect. It is also incorrect to say there is absolutely no evidence that drug A is better than drug B. However (and here I think we agree), the evidence for this is very weak. (The p-value here is probably around 0.5, not 1/3 as suggested by Limegreen, because confidence intervals for odds ratios are typically right

skewed

. This also means you can't just cmpare the lengths of the ranges 1.0-1.6 and 0.8-1.0. Taking logs avoids this issue.) So if there are any countervailing factors that would favor drug B (e.g. side effects, cost, study biases, or non-statistical reasons to believe B is more effective than A), they might easily tip the balance the other way. This is why people are generally careful not to read too much into such weak evidence. Ideally we would get more data to remove this uncertainty, shrinking the confidence interval enough that any uncertainty falls into a medically insignificant range, but clinical trials aren't cheap.

If you want to know the probability that drug A is better than drug B, confidence levels won't give you that. You need some basic Bayesian statistics instead. -- Avenue (talk) 13:01, 18 January 2008 (UTC)

Okay I get that what my colleague is essentially doing (without him being aware of it) is reducing the confidence interval and instead of believing the following (which is how I interpret it)...

"Okay - the 95% CI is not significant but if we look at the 65% (to use limegreen's figure or higher for avenue's) confidence interval then the lower limit does not cross 1.0. I therefore can state that I have an 65% (or higher) confidence that the true value lies within (but not exactly where within) this beneficial interval." - not hugely optimistic or likely to make me change practice.

Instead of that he is actually thinking (which seems a lot more optimistic and likely to change practice)...

"Okay - the 95% CI is not significant but despite this the probability of A being better than B is still 6:2 ((1.6-1.0):(1.0-0.8)) so that's great 'cos it's still an 3:1 chance of doing good rather than harm." In actual fact he really believes that the benefit is greater than 3:1 because he believes that the probability of the true value within the CI is normally distributed so the 0.8-1.0 represents only the left tail of the normal curve and he is comparing the areas under the curve.

My question is - are the 2 above standpoints both correct despite their superficial dissimilarities or are they mutually exclusive. I interpreted this wikipedia article to convey that CIs only give a confidence that the observer should have of the result rather than the probability per se. So what is the formal distinction between the two if any?Richard Shepherd (talk) 16:48, 18 January 2008 (UTC)

My confidence figure is lower (50%), not higher, than Limegreen's. Otherwise your view seems to be a correct

frequentist

interpretation of the data.

Your colleague seems to be interpreting the data by attempting to calculate something like a Bayes factor. They've assumed that the odds ratio is normally distributed, but (for a frequentist) it is right skewed. It's better to use the logarithm of the odds ratio (CI: -0.22 to 0.47) instead. Bayes factors also depend on details of the hypotheses you're comparing (and in particular a prior distribution for the difference in drug benefits), so the calculations aren't as simple as they say. But if these were done correctly, I suspect that the weight of evidence here would fall into Jeffreys' "barely worth mentioning" range (see Bayes factor). -- Avenue (talk) 23:29, 18 January 2008 (UTC)

I figured that odds ratios were probably skewed, but wasn't confident to punt on that :)

Somewhat in defence of hypothesis testing (and the relating arbitrariness of α=.05), even if after exhaustive calculation there was a 3:1 chance of doing good, there's still quite a high chance that you're doing bad.--Limegreen (talk) 01:46, 19 January 2008 (UTC)

Can any body tell me why the interval estimation better than point estimation?(shamsoon) —Preceding unsigned comment added by Shamsoon (talk • contribs) 14:53, 23 February 2008 (UTC)

inserted a little about this point in intro to article Melcombe (talk) 10:00, 26 February 2008 (UTC)

This "dispute" relates to the section "How to understand confidence intervals" and was put in by "Hubbardaie" (28 February 2008)

I thought I would start a section for discussing this.

Firstly there is the general question about including comparisons of frequentist and Bayesian approaches in this article when they might be better off as articles specifically for this comparison. I would prefer it not appearing in this article. I don't know if the same points are included in the existing frequentist vs Bayesian pages. Melcombe (talk) 16:46, 28 February 2008 (UTC)

Secondly, it seems that some of the arguments here may be essentially the same as that used for the third type of statistical inference -- fiducial inference -- which isn't mentioned as such. So possibly the "frequentist vs Bayesian" idea doesn't stand up. Melcombe (talk) 16:46, 28 February 2008 (UTC)

That fiducial intervals in some cases differ from confidence intervals was proved in 1936 by Bartlett in 1936. Michael Hardy (talk) 17:17, 28 February 2008 (UTC)

I agree that moving this part of the article somewhere might be approapriate. I'll review Bartlett but, as I recall, he wasn't making this exact argument. I believe the error here is to claim that P(a<x<b) is not a "real" probability because x is not a random variable. Acually, that is not a necessary criterion. Both a and b are random in the sense that they were computed from a set of samples which were selected from a population by a random process.Hubbardaie (talk) 17:27, 28 February 2008 (UTC)

Also, a frequentists holds only that the only meaning of "probability" is in regards to the frequency of occurances over a large number of trials. Consider a simple experiment for the measurement of a known parameter by random sampling (such as random sampling from a large population where we know the mean). Compute a 90% CI based on some sample size and we repeat this until we have a large number of separate 90% CI's each based on their own randomly selected samples. We will find, after sufficient trials, that the known mean of the population falls within 90% of the computed 90% CI's. So, even in a strict frequentist sense, P(a<x<b) is a "real" probability (at least the distinction, if there is a real distinction, has no bearing on observed reality).Hubbardaie (talk) 17:32, 28 February 2008 (UTC)

I think one version of a fiducial derivation is to argue that it is sensible to make the conversion from (X random, theta fixed) to (X fixed,theta random) directly without going via Bayes Theorem. I thought that was what was being done in this section of the article. Melcombe (talk) 18:05, 28 February 2008 (UTC)

Another thing we want to be careful of is that while some of the arguments were being made by respected statisticians like R.A. Fischer, these were views that were not widely adopted. And we need to separate out where the expert has waxed philisophically about a meaning and where he has come to a conclusion with a proof. At the very least, if a section introduces these more philisophical issues, it should not present it as if it were an uncontested and mathematically or empirically demonstrable fact.Hubbardaie (talk) 18:13, 28 February 2008 (UTC)

P(a<x<b)=0.9 is (more or less) the definition of a 90% confidence interval when a and b are considered random. But once you've calculated a particular confidence interval you've calculated particular values for a and b. In the example on the page at present, a = 82 - 1.645 = 80.355 and b = 82 + 1.645 = 83.645. 80.355 and 83.645 are clearly not random! So you can't say that P(80.355<x<83.645)=0.9, i.e. it's not true that the probability that x lies between 80.355 and 83.645 is 90%. This is related to the

prosecutor's fallacy as it's related to confusing P(parameter|statistic) with P(statistic|parameter). To relate the two you need a prior for P(parameter). If your prior is vague compared to the info from the data then the prior doesn't make a lot of difference, but that's not always the case. I'm sure I read a particularly clear explanation of this fairly recently and I'm going to rack my brains to try to remember where now.Qwfp (talk

) 18:40, 28 February 2008 (UTC)

I think fiducial inference is a historical distraction and mentions of it in the article should be kept to a very minimum. I think the general opinion is that it was a rare late blunder by Fisher (much like vitamin C was for Pauling). That's why I added this to the lead of fiducial inference recently (see there for ref):

In 1978, JG Pederson wrote that "the fiducial argument has had very limited success and is now essentially dead."

Qwfp (talk) 18:40, 28 February 2008 (UTC)

I think that you would find on a careful read of the prosecutors fallacy that it addresses a very different point and it would be misapplied in this case. I'm not confusing P(x|y) with P(y|x). I'm saying that experiments show that P(a<x<b) is equal to the frequency F(a < x < b) over a large number of trials (which is consistent with a "frequentist" position). On another note, no random number is random *once* it is chosen, but clearly a and b were computed from a process that included a random variable (the selection from the population) If I use a random number generator to generate a number between 0 and 1 with a uniform distribution, there is a 90% chance it will generate a value over .1. Once I have this number in front of me, it is an observed fact but *you* don’t yet know it. Would you say that P(x>.1) is not really a 90% probability because the actual number is no longer random (to me) or are you saying that its not really random because the “.1” wasn’t random? If we are going down the path of distinguishing what is “truly random” vs. “merely uncertain”, I would say we would have to solve some very big problems in physics, first. Even at a very fundamental level, is there a real difference between “random” and “uncertain” that can be differentiated by experiment? Apparently not. The “truly random” distinction won’t matter if nothing really is random or if there is no way to experimentally distinguish “true randomness” from observer-uncertainty. Hubbardaie (talk) 20:05, 28 February 2008 (UTC)

I've tracked down at least one source that i was half-remembering in my (rather hurried) contributions above, namely

• doi:10.1111/1467-9884.00238

On page 300 he writes:

"Again we have a contrast similar to the prosecutor's fallacy:

• confidence—probability that the interval includes θ;
• probability—probability that θ is included in the interval.

The former is a probability statement about the interval, given θ; the latter about θ, given the data. Practitioners frequently confuse the two."

I don't find his 'contrast' entirely clear as the difference between the phrases "probability that the interval includes θ" and "probability that θ is included in the interval" is only that of active vs passive voice; the two seem to mean the same to me. The sentence that follows that ("The former...") is clearer and gets to the heart of it I think. I accept it's not the same as the prosecutor's fallacy, but as Lindley says, it's similar.

I think one way to make the distinction clear is to point out that it's quite easy (if totally daft) to construct confidence intervals with any required coverage that don't even depend on the data. For instance, to get a 95% CI for a proportion (say, my chance of dying tomorrow) that I know has a continuous distribution with probability 0 of being exactly 1:

• Draw a random number between 0 and 1.
• If it's less than 0.95, the CI is [0,1].
• If it's greater than 0.95, the CI is [1,1], i.e. the single value 1 (the "interval" is a single point)

In the long run, 95% of the CIs include the true value, satisfying the definition of a CI. Say I do this and the random number happens to be 0.97. Can I say "there's a 95% probability that I'll die tomorrow" ?

Clearly no-one would use such a procedure to generate a confidence interval in practice. But you can end up with competing estimation procedures giving different confidence intervals for the same parameter, both of which are valid and have the same model assumptions, but the width of the CIs from one procedure varies more than those from the other procedure. (To choose between the two procedures, you might decide you prefer the one with the smaller average CI width). For example, say (0.1, 0.2) and (0.12, 0.18) are the CIs from the two procedures from the same data. But you can't then say both "there's 95% probability that the parameter lies between 0.10 and 0.20" and "there's 95% probability that the parameter lies between 0.12 and 0.18" i.e. they can't both be valid credible intervals.

Qwfp (talk) 22:46, 28 February 2008 (UTC) (PS Believe it or not after all that, I'm not in practice a Bayesian.)

Good, at least now we have a source. But I have two other very authoritative sources:A.A. Sveshnikov "Problems in Probability Theory, Mathematical Statistics and the Theory of Random Functions", 1968, Dover Books, pg 286 and a very good online source Wolframs's Mathmatica source site http://mathworld.wolfram.com/ConfidenceInterval.html. The former source states on pg 286 the following (Note: I could not duplicate some symbols exactly as Sveshnikov shows them, but I replaced them consistently so that the meaning is not altered)

"A Confidence interval is an interval that with a given confidence a covers a parameter θ to be estimated. The width of a symmetrical confidence interval 2e is determined by the condition P{|θ - θ'|<=e}=a, where θ' is the estimate of the parameter θ and the probability {emphasis added} P{|θ - θ'|<=e} is determined by the distribution law for θ'"

Here Sveshnikov makes it clear that he is usin the confidence interval as a statement of a probability. When we go to the Mathworld site it defines the confidence interval as:

"A confidence interval is an interval in which a measurement or trial falls corresponding to a given probability." {emphasis added}

I find other texts such as Morris DeGroot's "Optimal Statistical Decisions" pg 192-3 and Robert Serfling's "Approximation Theorems in Mathematical Statistics" pg 102-7 where confidence intervals are defined as P(LB<X<UB) {replacing their symbols with LB and UB}. It is made clear earlier in each text that the P(A) is the probability of A and the use of the same notation for the confidence interval apparently merits no further qualification.

On the other hand, even though none of my books within arm’s reach make the distinction Qwfp’s source makes, I found some other online sources that do attempt to make this distinction. When I search on ( “confidence interval”, definition, “probability that” ) I found that a small portion of the sites that come up make the distinction Qwfp’s source is proposing. Sites that make this distinction and sites that define confidence interval as a probability both include sources from academic institutions and what may be laymen. Although I see the majority of sites clearly defining a CI as a ‘’’probability’’’ that a parameter falls within an interval, I now see room for a possible dispute.

The problem is that the distinction made in this “philosophy of statistics” source and in other sources would seem to have no bearing on its use in practice. What specific decisions will be made incorrectly if this is interpreted one way or the other? Clearly, anyone can run an experiment on their own spreadsheet that shows that 90% of true means will fall within 90% CI’s when such CI’s are computed a large number of times. So what is the pragmatic effect?

I would agree to a section that, instead of matter-of-factly stating one side of this issue as the “truth”, simply points out the difference in different sources. To do otherwise would constitute original research.Hubbardaie (talk) 05:05, 29 February 2008 (UTC)

One maxim of out-and-out Bayesians is that "all probabilities are conditional probabilities", so if talking about probabilities, one should always make clear what those probabilities are conditioned on.

The key, I think, is to realise that Sveshnikov's statement means consideration of the probability P{(|θ - θ'|<=e) | θ }, i.e. the probability of that difference given θ, read off for the value θ = θ'. This is a different thing to the probability P{(|θ - θ'|<=e) | θ' }.

I think the phrase "read off for the value θ = θ' " is correct for defining a CI. But an alternative (more principed?) might be to quote the maximum value of |θ - θ'| s.t. P{(|θ - θ'|<=e) | θ } < a.

Either way, the wheels would still fall off in the example of the next section. Jheald (talk) 15:09, 29 February 2008

Sveshnikov said what he said. And I believe you are still mixing some unrelated issues about the philisophical position of Bayesian (which I prefer to call subjectivist) vs. frequentist view. Now we are going in circles, so just provide citations of the arguments you want to make. The only fair way to treat this is as a concept that lacks concensus even among authoritative sources. —Preceding unsigned comment added by Hubbardaie (talk • contribs) 29 February 2008

Here's an example I put up yesterday at Talk:Bayesian probability

Suppose you have a particle undergoing diffusion in a one degree of freedom space, so the probability distribution for it's position x at time t is given by

${\displaystyle P(x|t)dx={\frac {1}{\sqrt {2\pi \mu t}}}\exp {\frac {-x^{2}}{\mu t}}dx}$

Now suppose you observe the position of the particle, and you want to know how much time has elapsed.

It's easy to show that

${\displaystyle {\hat {t}}={\frac {x^{2}}{\mu }}}$

gives an

unbiased estimator

for t, since

${\displaystyle E({\hat {t}}|t)=t.}$

We can duly construct confidence limits, by considering for any given t what spread of values we would be likely (if we ran the experiment a million times) to see for ${\displaystyle {\hat {t}}}$.

So for example for t=1 we get a probability distribution of

${\displaystyle P(\;{\hat {t}}\;)d{\hat {t}}\propto {\sqrt {\hat {t}}}\exp {\frac {-{\hat {t}}}{\mu }}d{\hat {t}}}$

from which we can calculate lower and upper confidence limits -a and b, such that:

${\displaystyle P(-a<t-{\hat {t}}<b)=0.95}$

Having created such a table, suppose we now observe ${\displaystyle x={\sqrt {\mu }}}$. We then calculate ${\displaystyle {\hat {t}}=1}$, and report that we can state ${\displaystyle P({\hat {t}}-a<t<{\hat {t}}+b)}$ with 95% confidence, or that the "95% confidence range" is ${\displaystyle 1-a<t<1+b\;}$.

But that is not the same as calculating P(t|x).

The difference stands out particularly clearly, if we think what answer the method above would give, if the data came in that ${\displaystyle x=0\;}$.

From ${\displaystyle x=0\;}$ we find that ${\displaystyle {\hat {t}}=0}$. Now when t=0, the probability distribution for x is a delta-function at zero. So the distribution for ${\displaystyle {\hat {t}}}$ is also a delta-function at zero. So a and b are both zero, and so we must report a 100% confidence range, ${\displaystyle 0\leq t\leq 0}$.

On the other hand, what is the probability distribution for t given x? The particle might actually have returned to x=0 at any time. The likelihood function, given x=0, is

${\displaystyle L(t;x)={\frac {1}{\sqrt {2\pi \mu t}}}}$

Conclusion: data can come in, for which confidence intervals decidedly do not match Bayesian credible intervals for θ given the data, even with a flat prior on θ. Jheald (talk) 15:26, 29 February 2008 (UTC)

What about a weaker proposition, that given a particular parameter value, t = t*, the CI would accurately capture the parameter 95% of the time? Alas, this also is not necessarily true.

What is true is that a confidence interval for the difference ${\displaystyle {\hat {t}}-t}$ calculated for a correct value of t would accurately be met 95% of the time.

But that's not the confidence interval we're quoting. What we're actually quoting is the confidence interval that would pertain if the value of t were ${\displaystyle {\hat {t}}}$. But t almost certainly does not have that value; so we can no longer infer that the difference ${\displaystyle {\hat {t}}-t}$ will necessarily be in the CI 95% of the time, as it would if t did equal ${\displaystyle {\hat {t}}}$.

This can be tested straightforwardly, as per the request above for something that could be tested and plotted on a spreadsheet. Simply work out the CIs as a function of t for the diffusion model above; and then run a simulation to see how well it's calibrated for t=1. If the CIs are calculated as above, it becomes clear that those CIs exclude the true value of t a lot more than 5% of the time. Jheald (talk) 15:38, 29 February 2008 (UTC)

You make the same errors here that you made in the Bayesian talk. You show an example of a calculation for a partcular CI, then after that, simply leap to the original argument that the confidence of CI is not a P(a<x<b). You don't actually prove that point and, as my citations show, you would have to contradict at least some authoritative sources in that claim. All we can do is a balanced article that doesn't pretent that the claim "A 95% CI does not have a 95% probability of containing the true value" as an undisputed fact. It seems, again, more like a matter of an incoherent definition that can't possibly have any bearing on observations. But, again, let's just present all the relevant citations.Hubbardaie (talk) 16:18, 29 February 2008 (UTC)

Let's review things. I show an example where there is a 100% CI that a parameter equals zero; but the Likelihood function is

${\displaystyle L(t;x)={\frac {1}{\sqrt {2\pi \mu t}}}}$

Do you understand what that Likelihood function means? It means that the posterior probability P(t|data) will be different in all circumstances from a spike at t=0, unless you start off with absolute initial certainty that t=0.

That does prove the point that there is no necessity for the CI to have any connection with the probability P(a<t<b | data). Jheald (talk) 16:44, 29 February 2008 (UTC)

We are going in circles. I know exaclty wat Likelihood function means but my previous arguments already refute your conclusion. I just can't keep explaining it to you. Just show a citation for this argument and we'll move on from there.Hubbardaie (talk) 18:03, 29 February 2008 (UTC)

A confidence interval will in general only match a Bayesian credible interval (modulo the different worldviews), if

• (i) we can assume that we can adopt a uniform prior for the parameter;
• (ii) the function P(θ'|θ) is a symmetric function that depends only on (θ'-θ), with no other dependence on θ itself;
• and also (iii) that θ' is a sufficient statistic.

If those conditions are met (as they are, eg in Student's t test), then one can prove that P(a<t<b | data) = 0.95.

If they're not met, there's no reason at all to suppose P(a<t<b | data) = 0.95.

Furthermore, if (ii) doesn't hold, it's quite unlikely that you'll find, having calculated a and b given t', that {a<t<b} is true for 95% of cases. Try my example above, for one case in particular where it isn't. Jheald (talk) 18:45, 29 February 2008 (UTC)

Then, according to Sveshnikov and the other sources I cite, it is simply not a correctly computed CI, since the CI must meet the standard that the confidence IS the P(a<x<b). I repeat what I said above. Let's just lay out the proper citations and represent them all in the article. But I will work through your example in more detail. I think I can use an even more general way of describing possible solution spaces for CI's and whether for the set of all CI's over all populations, where we have no a priori knowledge of the population mean or variance, if P(a<x<c)is identical to the confidence. Perhaps you have found a fundamental error in the writings of some very respected reference sources in statistics. Perhaps not.Hubbardaie (talk) 22:53, 29 February 2008 (UTC)

After further review of the previous arguments and other research, I think I will concede a point to Jheald after all. Although I believe as Sveshnikov states, that a confidence interval should express a probability, not all procedures for computing a confidence interval will represent a true P(a<x<b) but only for two reasons:

1) Even though a large number of confidence intervals will be distributed such that the P(a<x<b)=the stated confidence, there will, by definition, be some that contradict prior knowledge. But in this case we will still find that such contradictions will apply to a small and unlikely set of 95% of CI's (by definition)

2) THere are situations, especially in small samples, where 95% confidence intervals contradict prior knowledge even to the extent that a large number of 95% CI's will not contain the answer 95% of the time. In these cases it seems to be because prior knowledge contradicts the assumptions in the procedure used to compute the CI. In effect, an incorrectly computed CI. For example, suppose I have a population distributed between 0 and 1 by a function F(X^3) where X is a uniformly distributed random varialbe between 0 and 1. CI's computed with small samples using the t-stat will produce distributions that allow for negative values even when we know the population can't produce that. Furthermore, this effect cannot be made up for by computing a large number of CI's with separate random samples. Less than 95% of the computed 95% CI's will contain the true population mean.

The reason, I think, Sveshnikov and others still say that CI do, in fact, represent a probablity P(a<x<b) is because that is the objective, by definition, and that where we choose sample statistics based assumptions that a priori knowledge contradict, we should not be surprise we produced the wrong answer. So Sveshnikov et al would, I argue, just say we picked the wrong method to compute the CI and that the ojective should always be to produce a CI that has a P(a<x<b) as stated. We have simply pointed out the key shortcoming of non-Bayesian methods when we know certain things about the population which don't match the assumptions of the sampling statistic. So, even this concession doesn't exactly match everything Jheald was arguing, I can see where he was right in this area. Thanks for the interesting discussion.Hubbardaie (talk) 17:38, 1 March 2008 (UTC)

The comment(s) below were originally left at Talk:Confidence interval/Comments, and are posted here for posterity. Following

22:40, 16 June 2007 (UTC)

I appreciate all the advanced mathematics, but it would be nice to see a section where there is an example of an actual, simple CI done. Also in the section "How to understand confidence intervals," it would be nice to see what the tempting misunderstanding is before all the equations. Ibrmrn (talk) 22:22, 5 December 2007 (UTC)

Last edited at 22:24, 5 December 2007 (UTC). Substituted at 20:20, 2 May 2016 (UTC)