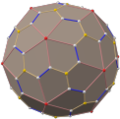
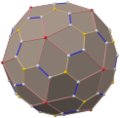
Truncated icosahedron

Source: Wikipedia, the free encyclopedia.

Truncated icosahedron
TypeArchimedean solid
Uniform polyhedron
Goldberg polyhedron
Faces32
Edges90
Vertices60
Symmetry groupIcosahedral symmetry
Dual polyhedronPentakis dodecahedron
Vertex figure
Net
3D model of a truncated icosahedron

In geometry, the truncated icosahedron is a polyhedron that can be constructed by truncating all of the regular icosahedron's vertices. Intuitively, it may be regarded as footballs (or soccer balls) that are typically patterned with white hexagons and black pentagons. It can be found in the application of geodesic dome structures such as those whose architecture Buckminster Fuller pioneered are often based on this structure. It is an example of an Archimedean solid, as well as a Goldberg polyhedron.

Construction

The truncated icosahedron can be constructed from a regular icosahedron by cutting off all of its vertices, known as truncation. Each of the 12 vertices at the one-third mark of each edge creates 12 pentagonal faces and transforms the original 20 triangle faces into regular hexagons.[1] Therefore, the resulting polyhedron has 32 faces, 90 edges, and 60 vertices.[2] A Goldberg polyhedron is one whose faces are 12 pentagons and some multiple of 10 hexagons. There are three classes of Goldberg polyhedron, one of them is constructed by truncating all vertices repeatedly, and the truncated icosahedron is one of them, denoted as .[3]

Properties

The surface area and the volume of the truncated icosahedron of edge length are:[2] The sphericity of a polyhedron describes how closely a polyhedron resembles a sphere. It can be defined as the ratio of the surface area of a sphere with the same volume to the polyhedron's surface area, from which the value is between 0 and 1. In the case of a truncated icosahedron, it is:[2]

The dihedral angle of a truncated icosahedron between adjacent hexagonal faces is approximately 138.18°, and that between pentagon-to-hexagon is approximately 142.6°.[4]

The truncated icosahedron is an

vertex-transitivity.[6][7] The polygonal faces that meet for every vertex are one pentagon and two hexagons, and the vertex figure
of a truncated icosahedron is . The truncated icosahedron's dual is pentakis dodecahedron, a Catalan solid,[8] shares the same symmetry as the truncated icosahedron.[9]

Truncated icosahedral graph

The truncated icosahedral graph

According to

convex polyhedron, can be represented as a polyhedral graph, meaning a planar graph (one that can be drawn without crossing edges) and 3-vertex-connected graph (remaining connected whenever two of its vertices are removed).[10] The graph is known as truncated icosahedral graph, and it has 60 vertices and 90 edges. It is an Archimedean graph because it resembles one of the Archimedean solids. It is a cubic graph, meaning that each vertex is incident to exactly three edges.[11][12][13]

Appearance

The truncated icosahedron (left) compared with an association football

The balls used in

2006.[16]

The buckminsterfullerene molecule

atomic bombs.[18] Its structure can also be found in the protein of clathrin.[13]

Piero della Francesca's image of a truncated icosahedron from his book De quinque corporibus regularibus

The truncated icosahedron was known to

Harmonices Mundi.[20]

See also

References

  1. ISBN 978-0-691-22534-0
    .
  2. ^
    MR 0290245
    .
  3. ISBN 978-0-387-92713-8
    .
  4. Zbl 0132.14603
    .
  5. ISBN 978-3-319-64123-2
    .
  6. ^ Koca, M.; Koca, N. O. (2013). "Coxeter groups, quaternions, symmetries of polyhedra and 4D polytopes". Mathematical Physics: Proceedings of the 13th Regional Conference, Antalya, Turkey, 27–31 October 2010. World Scientific. p. 48.
  7. ISBN 978-0-521-55432-9
    .
  8. ISBN 978-0-486-23729-9
    .
  9. ISBN 9780486268514
    .
  10. ISBN 978-3-319-30451-9
    .
  11. ^ Read, R. C.; Wilson, R. J. (1998). An Atlas of Graphs. Oxford University Press. p. 268.
  12. ^ Godsil, C.; Royle, G. (2001). Algebraic Graph Theory. New York: Springer-Verlag. p. 211.
  13. ^ a b Kostant, B. (1995). "The Graph of the Truncated Icosahedron and the Last Letter of Galois" (PDF). Notices of the American Mathematical Society. 42 (9): 959–968.
  14. doi:10.1511/2006.60.350
    .
  15. ISBN 978-1-4504-9679-7
    .
  16. ISBN 9789811237126
    .
  17. ISBN 978-0-444-52844-5
    .
  18. ISBN 0-684-82414-0
    .
  19. ^ Katz, Eugene A. (2011). "Bridges between mathematics, natural sciences, architecture and art: case of fullerenes". Art, Science, and Technology: Interaction Between Three Cultures, Proceedings of the First International Conference. pp. 60–71.
  20. S2CID 118516740
    .
Wikimedia Commons has media related to Truncated icosahedron.
Look up truncated icosahedron in Wiktionary, the free dictionary.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Truncated_icosahedron&oldid=1281646980"