This is the user sandbox of Danko Georgiev. A user sandbox is a subpage of the user's user page. It serves as a testing spot and page development space for the user and is not an encyclopedia article. Create or edit your own sandbox here. Other sandboxes: Main sandbox | Template sandbox Finished writing a draft article? Are you ready to request review of it by an experienced editor for possible inclusion in Wikipedia? Submit your draft for review!

Trigonometric Proof of the

Pythagorean Theorem

by Jackson and Johnson (2023)

On March 18, 2023, two high school students, Ne'Kiya D. Jackson and Calcea Rujean Johnson, from

In 2009, Jason Zimba has published a trigonometric proof of the

^: 275

The trigonometric proof by Jackson and Johnson uses a beautiful geometric construction, repeated application of the trigonometric definition of the sine function, and summation of infinite geometric series[4]^[5][1]. Thus, the Jackson and Johnson proof is different from the proof presented by Zimba.^[3]

Ingredients of the proof

All of these ingredients do not presuppose the validity of the Pythagorean theorem, but when combined imply that the Pythagorean theorem is true:

• Trigonometric definition of
  sine as a dimensionless
  ratio of opposite side to hypotenuse : does not presuppose that right triangles are drawn upon "flat" surface
• Euclid's parallel postulate : introduces the "flat" geometric space and "similarity" so that "${\displaystyle \sin \alpha }$ in a given right triangle (with angles ${\displaystyle \alpha ,{\frac {\pi }{2}}-\alpha ,{\frac {\pi }{2}}}$)" can be proved to be equal to the "${\displaystyle \sin \alpha }$ defined as ratio in any other similar (i.e. "scaled") right triangle (with angles ${\displaystyle \alpha ,{\frac {\pi }{2}}-\alpha ,{\frac {\pi }{2}}}$ )"
• Law of sines
• Basic arithmetic rules
• Rule for summation of geometric series

Steps of the actual proof

The proof by Jackson and Johnson is valid for almost all right triangles, except for the case when ${\displaystyle a=b}$, i.e. Isosceles Right Triangle.

Case I

For the case when ${\displaystyle a\neq b}$, we can always choose to orient the right triangle ${\displaystyle \triangle ABC}$ so that a<b as shown in the figure.

Step 1: Then we reflect the right triangle to obtain point D. We extend leg BE perpendicular to AB, and extend AD until it crosses BE. From Euclid's parallel postulate, it is guaranteed that AD will cross BE because ${\displaystyle 2\alpha <{\frac {\pi }{2}}}$.

Step 2: we apply repeatedly the trigonometric definition of

as ratio of opposite side to hypotenuse in order to compute the lengths of the line segments that sum up to AE or BE.

Step 3: we need to sum convergent infinite geometric series where ${\displaystyle {\frac {a^{2}}{b^{2}}}<1}$ in order to compute ${\displaystyle \sin \left(2\alpha \right)}$ from the large right triangle ${\displaystyle \triangle ABE}$:

${\displaystyle \sin \left(2\alpha \right)={\frac {\overline {BE}}{\overline {AE}}}={\frac {2c{\frac {a}{b}}\left(1+{\frac {a^{2}}{b^{2}}}+\left({\frac {a^{2}}{b^{2}}}\right)^{2}+\left({\frac {a^{2}}{b^{2}}}\right)^{3}+\ldots \right)}{c+2c{\frac {a^{2}}{b^{2}}}\left(1+{\frac {a^{2}}{b^{2}}}+\left({\frac {a^{2}}{b^{2}}}\right)^{2}+\left({\frac {a^{2}}{b^{2}}}\right)^{3}+\ldots \right)}}={\frac {2c{\frac {a}{b}}\left({\frac {1}{1-{\frac {a^{2}}{b^{2}}}}}\right)}{c+2c{\frac {a^{2}}{b^{2}}}\left({\frac {1}{1-{\frac {a^{2}}{b^{2}}}}}\right)}}={\frac {2ab}{a^{2}+b^{2}}}}$

Step 4: we employ the Law of sines in ${\displaystyle \triangle ABD}$ to find out:

${\displaystyle {\frac {2a}{\sin \left(2\alpha \right)}}={\frac {c}{\sin \beta }}}$

Step 5: upon substituion with ${\displaystyle \sin \beta ={\frac {b}{c}}}$ and ${\displaystyle \sin \left(2\alpha \right)={\frac {\overline {BE}}{\overline {AE}}}}$, and after application of basic arithmetic operations (which we have used also in previous steps), we obtain the Pythagorean theorem:

${\displaystyle a^{2}+b^{2}=c^{2}}$.

Case II

For the special case when ${\displaystyle a=b}$ (hence ${\displaystyle \alpha =\beta ={\frac {\pi }{4}}}$), the geometric series does not converge because ${\displaystyle {\frac {a^{2}}{b^{2}}}=1}$ and also AE does not intersect BE because ${\displaystyle \alpha +\beta +2\alpha =\pi }$. However, the proof of the Pythagorean theorem becomes purely algebraic using the areas of triangles ${\displaystyle \triangle ABC}$, ${\displaystyle \triangle ACD}$ and ${\displaystyle \triangle ABD}$, namely: ${\displaystyle {\frac {ab}{2}}+{\frac {ab}{2}}={\frac {c^{2}}{2}}}$, but since ${\displaystyle a=b}$, it follows that ${\displaystyle {\frac {a^{2}}{2}}+{\frac {b^{2}}{2}}={\frac {c^{2}}{2}}}$.

Nonexistence of trigonometric proofs of the

Pythagorean Theorem claimed by Elisha Scott Loomis

Loomis has dedicated a special section on page 244 in his book in order to state in all caps that there are "NO TRIGONOMETRIC PROOFS"[2]:

NO TRIGONOMETRIC PROOFS

Facing forward the thoughtful reader may raise the question: Are there any proofs based upon the science of trigonometry or analytical geometry?

There are no trigonometric proofs, because all the fundamental formulae of trigonometry are themselves based upon the truth of the Pythagorean Theorem; because of this theorem we say ${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$, etc. Trigonometry is because the Pythagorean Theorem is.

This shows poor understanding by Elisha Scott Loomis of what trigonometry is. The trigonometric functions sine and cosine are usually defined (in high school textbooks) as ratio of two sides inside a right triangle and do not necessitate any knowledge of the equality ${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$.

The proof by Zimba^[3] derives the equality ${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$ from sine and cosine subtraction formulas. Then, he correctly shows that the

from the equality ${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$. Conversely, the equality ${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$ can also be derived as a corollary from the occurs only when ${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$ is assumed to be true without proof, but circular reasoning does not occur if ${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$ is first proved and then used for deducing the Pythagorean Theorem.

${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1\qquad \Leftrightarrow \qquad {\frac {a^{2}}{c^{2}}}+{\frac {b^{2}}{c^{2}}}={\frac {c^{2}}{c^{2}}}}$

Nevertheless, a "stubborn" advocate of Loomis may object that Zimba is deriving circularly the Pythagorean Theorem from exactly the equality ${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$. Thus, the main point is that Zimba's proof has no whatsoever power over "stubborn" advocates of Loomis.

The novelty and power of the trigonometric proof by Jackson and Johnson is that it never needs to use the equality ${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$, hence it achieves what "stubborn" advocates of Loomis claim is "impossible". This indeed justifies the provocatively chosen title of their presentation: "An Impossible Proof Of Pythagoras".^[1]

Improved Jackson-Johnston proof based on Einstein's construction

The strategy of Jackson-Johnston trigonometric proof can be simplified if combined with Einstein's construction. The simplification proceeds by noting that instead of doubling the angle to ${\displaystyle 2\alpha }$, we can complete it to ${\displaystyle \alpha +\beta ={\frac {\pi }{2}}}$. Then, we eliminate the need of considering summation of infinite geometric series and we no longer need the law of sines.

From the trigonometric definitions of sines inside triangle ${\displaystyle \triangle ABC}$, we have ${\displaystyle \sin \alpha ={\frac {a}{c}}}$ and ${\displaystyle \sin \beta ={\frac {b}{c}}}$.

For the sides in triangle ${\displaystyle \triangle ACD}$, we have ${\displaystyle {\overline {AD}}={\frac {b}{\sin \alpha }}={\frac {bc}{a}}}$ and ${\displaystyle {\overline {CD}}=b{\frac {\sin \beta }{\sin \alpha }}={\frac {b^{2}}{a}}}$.

From the triangle ${\displaystyle \triangle ABD}$, we have:

${\displaystyle {\frac {c}{a+{\frac {b^{2}}{a}}}}=\sin \alpha }$

Substitution of ${\displaystyle \sin \alpha ={\frac {a}{c}}}$ followed by simple algebraic transformations gives:

${\displaystyle {\frac {c}{a+{\frac {b^{2}}{a}}}}={\frac {a}{c}}}$

${\displaystyle c^{2}=a\left(a+{\frac {b^{2}}{a}}\right)}$

${\displaystyle c^{2}=a^{2}+b^{2}}$

It is important to note that in contrast to the original construction by Jackson-Johnston which is invalid for ${\displaystyle a=b}$, the improved construction that completes the angle to ${\displaystyle \alpha +\beta ={\frac {\pi }{2}}}$ is valid for all possible cases of ${\displaystyle a}$ and ${\displaystyle b}$.

Difference between trigonometric and analytic definitions of "sine"

The high school definition of trigonometric function "sine" as dimensionless ratio of opposite side to hypotenuse inside a right triangle is curvature-dependent, and is not equivalent to the analytic definition of the "sine" function using Taylor series, which is curvature-independent.

Only in flat space, the trigonometric definition of "sine" as ratio of sides

${\displaystyle \sin \alpha :={\frac {a}{c}}}$

is equivalent to the analytic definition of the "sine" using Taylor series:

${\displaystyle \sin \alpha :=\alpha -{\frac {\alpha ^{3}}{3!}}+{\frac {\alpha ^{5}}{5!}}-{\frac {\alpha ^{7}}{7!}}+\ldots }$

In curved space, the two definitions produce different quantities, so they are not equivalent.

Why these two definitions are not equivalent?

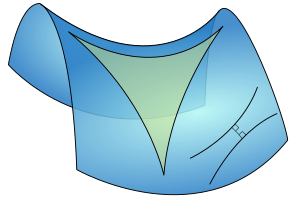
Because the geometric expression ${\displaystyle {\frac {a}{c}}}$ is curvature-dependent, whereas the algebraic expression ${\displaystyle \alpha -{\frac {\alpha ^{3}}{3!}}+{\frac {\alpha ^{5}}{5!}}-{\frac {\alpha ^{7}}{7!}}+\ldots }$ is curvature-independent. A visual way to see it, is to draw a right triangle on a

and notice that the ratio of the side ${\displaystyle a}$ and hypotenuse ${\displaystyle c}$ has nothing to do with the analytic "sine".

How to verify that these two definitions are not equivalent?

Easy with dimensional analysis: the side length ${\displaystyle a(m)}$ has units of meters, and the hypotenuse ${\displaystyle c(m)}$ has units of meters, so

${\displaystyle \sin \alpha :={\frac {a(m)}{c(m)}}}$

In contrast, in the analytic expression ${\displaystyle \alpha (1)}$ is dimensionless quantity, i.e., pure number

${\displaystyle \sin \alpha :=\alpha (1)-{\frac {\alpha (1)^{3}}{3!}}+{\frac {\alpha (1)^{5}}{5!}}-{\frac {\alpha (1)^{7}}{7!}}+\ldots }$

The above implies that only the expression in which "meters" appear is curvature-dependent. Thus, "trigonometric proofs" of the Pythagorean theorem are not "circular" as long as they use the trigonometric definition of "sine" as ratio of two sides.

Alternative way to see that "there is a difference" in the two definitions is to count the number of

${\displaystyle f(a,c)}$, whereas the analytic expression is a single-variable function and has only one argument ${\displaystyle f(\alpha )}$.

Why should Wikipedia care?

Because the article should be accessible to high school students.

Is "sine squared" plus "cosine squared" equal to 1 in hyperbolic geometry?

There are definitely two non-equivalent definitions of the "sine" and "cosine" functions inside the article on

flat

.

"Trigonometric" sine and cosine in high school are defined as trigonometric ratios

${\displaystyle {\boldsymbol {\mathbf {\sin } }}\alpha :={\frac {a}{c}}}$

${\displaystyle {\boldsymbol {\cos }}\alpha :={\frac {b}{c}}}$

These trigonometric functions are written in bold font for distinction from the subsequent "analytic definition", symbol ${\displaystyle :=}$ means "is equal by definition.

The Pythagorean theorem is

${\displaystyle \left({\frac {a}{c}}\right)^{2}+\left({\frac {b}{c}}\right)^{2}={\boldsymbol {\mathbf {\sin } }}^{2}\alpha +{\boldsymbol {\cos }}^{2}\alpha =1}$

"Analytic" functions sine and cosine are defined as Taylor series

${\displaystyle \sin \alpha :=\alpha -{\frac {\alpha ^{3}}{3!}}+{\frac {\alpha ^{5}}{5!}}-{\frac {\alpha ^{7}}{7!}}+\ldots =\sum _{k=0}^{\infty }{\frac {\left(-1\right)^{k}\alpha ^{2k+1}}{\left(2k+1\right)!}}}$

${\displaystyle \cos \alpha :=1-{\frac {\alpha ^{2}}{2!}}+{\frac {\alpha ^{4}}{4!}}-{\frac {\alpha ^{6}}{6!}}+\ldots =\sum _{k=0}^{\infty }{\frac {\left(-1\right)^{k}\alpha ^{2k}}{\left(2k\right)!}}}$

Because the sine and cosine series are

absolutely convergent

, we can easily compute the squares of these series by multiplication and suitable rearrangement of the infinite terms

${\displaystyle \sin ^{2}\alpha =\alpha ^{2}-{\frac {\alpha ^{4}}{3}}+{\frac {2\alpha ^{6}}{45}}-{\frac {\alpha ^{8}}{315}}+\ldots =-\sum _{k=1}^{\infty }{\frac {\left(-1\right)^{k}2^{2k-1}\alpha ^{2k}}{\left(2k\right)!}}}$

${\displaystyle \cos ^{2}\alpha =1-\alpha ^{2}+{\frac {\alpha ^{4}}{3}}-{\frac {2\alpha ^{6}}{45}}+{\frac {\alpha ^{8}}{315}}-\ldots =1+\sum _{k=1}^{\infty }{\frac {\left(-1\right)^{k}2^{2k-1}\alpha ^{2k}}{\left(2k\right)!}}}$

Now summing the latter two analytic expressions, we obtain

${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =-\sum _{k=1}^{\infty }{\frac {\left(-1\right)^{k}2^{2k-1}\alpha ^{2k}}{\left(2k\right)!}}+1+\sum _{k=1}^{\infty }{\frac {\left(-1\right)^{k}2^{2k-1}\alpha ^{2k}}{\left(2k\right)!}}=1}$

The remarkable fact is that the analytic identity, ${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$, is always true algebraically regardless of the curvature or flatness of the geometry!

Finally, provided with perfectly explicit and non-ambiguous notation, let us investigate the Pythagorean theorem and the definitions of trigonometric functions in absolute geometry in which Euclid's 5th parallel postulate is not true. If you want a concrete such example, consider hyperbolic geometry inside which we have the following:

The Pythagorean theorem is false

${\displaystyle a^{2}+b^{2}<c^{2}}$

The Pythagorean identity is false

${\displaystyle \left({\frac {a}{c}}\right)^{2}+\left({\frac {b}{c}}\right)^{2}={\boldsymbol {\mathbf {\sin } }}^{2}\alpha +{\boldsymbol {\cos }}^{2}\alpha <1}$

However the analytic identity is true

${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1}$

Without explicitly stating that there are 2 non-equivalent definitions of sine and cosine, which have different dependence on the curvature of the geometry, it is impossible to answer meaningfully the question: Is "sine squared" plus "cosine squared" equal to 1 in hyperbolic geometry?

References

1. ^ ^{a b c} Jackson, Ne'Kiya D. and Johnson, Calcea Rujean (2023). "An Impossible Proof Of Pythagoras". AMS Special Session on Undergraduate Mathematics and Statistics Research, I: SS30A.{{cite journal}}: CS1 maint: multiple names: authors list (link)
2. ^ ^{a b} Loomis, Elisha Scott (1968). The Pythagorean Proposition. Washington, D.C.: National Council of Teachers of Mathematics.
3. ^ ^{a b c} Zimba, Jason (2009). "On the possibility of trigonometric proofs of the Pythagorean theorem". Forum Geometricorum. 9: 275–278.
4. ^ WWL-TV (March 23, 2023). "New Orleans teens make mathematical discovery unproven for 2,000 years". New Orleans, Louisiana. WWL-TV Channel 4, Eyewitness News, CBS affiliate in New Orleans. Retrieved 2023-04-02.
5. ^ Ramon Antonio Vargas (March 24, 2023). "US teens say they have new proof for 2,000-year-old mathematical theorem". The Guardian.