Relaxation oscillator

The first relaxation oscillator circuit, the

• Sawtooth, sweep, or flyback oscillator: In this type the energy storage capacitor is charged slowly but discharged rapidly, essentially instantly, by a short circuit through the switching device. Thus there is only one "ramp" in the output waveform which takes up virtually the entire period. The voltage across the capacitor approximates a sawtooth wave, while the current through the switching device is a sequence of short pulses.
• Astable multivibrator: In this type the capacitor is both charged and discharged slowly through a resistor, so the output waveform consists of two parts, an increasing ramp and a decreasing ramp. The voltage across the capacitor approximates a triangle waveform
  , while the current through the switching device approximates a square wave.

Before the advent of microelectronics, simple relaxation oscillators often used a negative resistance device with hysteresis such as a thyratron tube,^[22] neon lamp,^[22] or unijunction transistor, however today they are more often built with dedicated integrated circuits such as the 555 timer chip.

Applications

Relaxation oscillators are generally used to produce low

This example can be implemented with a

If the threshold element is a neon lamp,^{[nb 1][nb 2]} the circuit also provides a flash of light with each discharge of the capacitor. This lamp example is depicted below in the typical circuit used to describe the Pearson–Anson effect. The discharging duration can be extended by connecting an additional resistor in series to the threshold element. The two resistors form a voltage divider; so, the additional resistor has to have low enough resistance to reach the low threshold.

Alternative implementation with 555 timer

A similar relaxation oscillator can be built with a 555 timer IC (acting in astable mode) that takes the place of the neon bulb above. That is, when a chosen capacitor is charged to a design value, (e.g., 2/3 of the power supply voltage) comparators within the 555 timer flip a transistor switch that gradually discharges that capacitor through a chosen resistor (which determine the RC time constant) to ground. At the instant the capacitor falls to a sufficiently low value (e.g., 1/3 of the power supply voltage), the switch flips to let the capacitor charge up again. The popular 555's comparator design permits accurate operation with any supply from 5 to 15 volts or even wider.

Other, non-comparator oscillators may have unwanted timing changes if the supply voltage changes.

Inductive oscillator

A blocking oscillator using the inductive properties of a pulse transformer to generate square waves by driving the transformer into saturation, which then cuts the transformer supply current until the transformer unloads and desaturates, which then triggers another pulse of supply current, generally using a single transistor as the switching element.

Comparator–based relaxation oscillator

Alternatively, when the capacitor reaches each threshold, the charging source can be switched from the positive power supply to the negative power supply or vice versa. The earlier inverting Schmitt trigger animated example operates on the same principle (since the Schmitt trigger internally performs comparison). This section will analyze a similar implementation using a comparator as a discrete component.

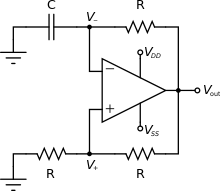
This relaxation oscillator is a hysteretic oscillator, named this way because of the

General concept

The system is in unstable equilibrium if both the inputs and outputs of the comparator are at zero volts. The moment any sort of noise, be it thermal or electromagnetic noise brings the output of the comparator above zero (the case of the comparator output going below zero is also possible, and a similar argument to what follows applies), the positive feedback in the comparator results in the output of the comparator saturating at the positive rail.

In other words, because the output of the comparator is now positive, the non-inverting input to the comparator is also positive, and continues to increase as the output increases, due to the voltage divider. After a short time, the output of the comparator is the positive voltage rail, ${\displaystyle V_{DD}}$.

The inverting input and the output of the comparator are linked by a series RC circuit. Because of this, the inverting input of the comparator asymptotically approaches the comparator output voltage with a time constant RC. At the point where voltage at the inverting input is greater than the non-inverting input, the output of the comparator falls quickly due to positive feedback.

This is because the non-inverting input is less than the inverting input, and as the output continues to decrease, the difference between the inputs gets more and more negative. Again, the inverting input approaches the comparator's output voltage asymptotically, and the cycle repeats itself once the non-inverting input is greater than the inverting input, hence the system oscillates.

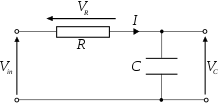
Example: Differential equation analysis of a comparator-based relaxation oscillator

${\displaystyle \,\!V_{+}}$ is set by ${\displaystyle \,\!V_{\rm {out}}}$ across a resistive voltage divider:

${\displaystyle V_{+}={\frac {V_{\rm {out}}}{2}}}$

${\displaystyle \,\!V_{-}}$ is obtained using Ohm's law and the capacitor differential equation:

${\displaystyle {\frac {V_{\rm {out}}-V_{-}}{R}}=C{\frac {dV_{-}}{dt}}}$

Rearranging the ${\displaystyle \,\!V_{-}}$ differential equation into standard form results in the following:

${\displaystyle {\frac {dV_{-}}{dt}}+{\frac {V_{-}}{RC}}={\frac {V_{\rm {out}}}{RC}}}$

Notice there are two solutions to the differential equation, the driven or particular solution and the homogeneous solution. Solving for the driven solution, observe that for this particular form, the solution is a constant. In other words, ${\displaystyle \,\!V_{-}=A}$ where A is a constant and ${\displaystyle {\frac {dV_{-}}{dt}}=0}$.

${\displaystyle {\frac {A}{RC}}={\frac {V_{\rm {out}}}{RC}}}$

${\displaystyle \,\!A=V_{\rm {out}}}$

Using the Laplace transform to solve the homogeneous equation ${\displaystyle {\frac {dV_{-}}{dt}}+{\frac {V_{-}}{RC}}=0}$ results in

${\displaystyle V_{-}=Be^{{\frac {-1}{RC}}t}}$

${\displaystyle \,\!V_{-}}$ is the sum of the particular and homogeneous solution.

${\displaystyle V_{-}=A+Be^{{\frac {-1}{RC}}t}}$

${\displaystyle V_{-}=V_{\rm {out}}+Be^{{\frac {-1}{RC}}t}}$

Solving for B requires evaluation of the initial conditions. At time 0, ${\displaystyle V_{\rm {out}}=V_{dd}}$ and ${\displaystyle \,\!V_{-}=0}$. Substituting into our previous equation,

${\displaystyle \,\!0=V_{dd}+B}$

${\displaystyle \,\!B=-V_{dd}}$

Frequency of oscillation

First let's assume that ${\displaystyle V_{dd}=-V_{ss}}$ for ease of calculation. Ignoring the initial charge up of the capacitor, which is irrelevant for calculations of the frequency, note that charges and discharges oscillate between ${\displaystyle {\frac {V_{dd}}{2}}}$ and ${\displaystyle {\frac {V_{ss}}{2}}}$. For the circuit above, V_ss must be less than 0. Half of the period (T) is the same as time that ${\displaystyle V_{\rm {out}}}$ switches from V_dd. This occurs when V₋ charges up from ${\displaystyle -{\frac {V_{dd}}{2}}}$ to ${\displaystyle {\frac {V_{dd}}{2}}}$.

${\displaystyle V_{-}=A+Be^{{\frac {-1}{RC}}t}}$

${\displaystyle {\frac {V_{dd}}{2}}=V_{dd}\left(1-{\frac {3}{2}}e^{{\frac {-1}{RC}}{\frac {T}{2}}}\right)}$

${\displaystyle {\frac {1}{3}}=e^{{\frac {-1}{RC}}{\frac {T}{2}}}}$

${\displaystyle \ln \left({\frac {1}{3}}\right)={\frac {-1}{RC}}{\frac {T}{2}}}$

${\displaystyle \,\!T=2\ln(3)RC}$

${\displaystyle \,\!f={\frac {1}{2\ln(3)RC}}}$

When V_ss is not the inverse of V_dd we need to worry about asymmetric charge up and discharge times. Taking this into account we end up with a formula of the form:

${\displaystyle T=(RC)\left[\ln \left({\frac {2V_{ss}-V_{dd}}{V_{ss}}}\right)+\ln \left({\frac {2V_{dd}-V_{ss}}{V_{dd}}}\right)\right]}$

Which reduces to the above result in the case that ${\displaystyle V_{dd}=-V_{ss}}$.

See also

• Multivibrator
• FitzHugh–Nagumo model – A hysteretic model of, for example, a neuron.
• Schmitt trigger – The circuit on which the comparator-based relaxation oscillator is based.
• Unijunction transistor – A transistor capable of relaxation oscillations.
• Robert Kearns – Used relaxation oscillator in intermittent wiper patent dispute.
• Limit cycle – Mathematical model used to analyze relaxation oscillations

Notes

References

1. ISBN 0750698667
   .
2. ^ ^{a b c d} Edson, William A. (1953). Vacuum Tube Oscillators (PDF). New York: John Wiley and Sons. p. 3. on Peter Millet's Tubebooks website
3. ISBN 0122004000
   .
4. ^
   ISBN 978-1139485760
   .
5. doi:10.1109/9.898696
   . Retrieved February 22, 2014.
6. ^ Nave, Carl R. (2014). "Relaxation Oscillator Concept". HyperPhysics. Dept. of Physics and Astronomy, Georgia State Univ. Retrieved February 22, 2014. {{cite web}}: External link in |work= (help)
7. ISBN 978-1402085161
   .
8. ^ DeLiang, Wang (1999). "Relaxation oscillators and networks" (PDF). Wiley Encyclopedia of Electrical and Electronics Engineering, Vol. 18. Wiley & Sons. pp. 396–405. Retrieved February 2, 2014.
9. ^ ^{a b c} Sauro, Herbert M. (2009). "Oscillatory Circuits" (PDF). Class notes on oscillators: Systems and Synthetic Biology. Sauro Lab, Center for Synthetic Biology, University of Washington. Retrieved November 12, 2019.,
10. ISBN 978-9814374422
    .
11. ^
    S2CID 293369
    . Retrieved December 24, 2014.
12. ^
    ISBN 0817642234
    .
13. ^
    ISBN 978-0521033336
    .
14. ^ ^{a b c} Pippard, The Physics of Vibration, p. 41-42
15. ISBN 978-0123972996
    . Retrieved February 24, 2014.
16. ISBN 0906048966
    .
17. doi:10.1051/jphystap:019190090021100
    .
18. ^
    S2CID 293369
    .
19. ^ van der Pol, B. (1920). "A theory of the amplitude of free and forced triode vibrations". Radio Review. 1: 701–710, 754–762.
20. doi:10.1080/14786442608564127
    .
21. ^ Shukla, Jai Karan N. (1965). "Discontinuous Theory of Relaxation Oscillators". Master of Science thesis. Dept. of Electrical Engineering, Kansas State Univ. Retrieved February 23, 2014. {{cite journal}}: Cite journal requires |journal= (help)
22. ^ ^{a b c} Puckle, O. S. (1951). Time Bases (Scanning Generators), 2nd Ed. London: Chapman and Hall, Ltd. pp. 15–27.
23. ^
    ISBN 9780780311497
    . Retrieved 2015-09-22.
24. ^
    ISBN 0306487160
    .
25. ^ "Shaw Communications".

Wikimedia Commons has media related to Relaxation oscillators.