Snub disphenoid

Snub disphenoid
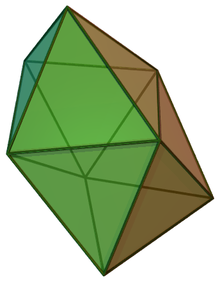Type	Deltahedron Johnson J83 – J84 – J85
Faces	12 triangles
Edges	18
Vertices	8
Vertex configuration	${\displaystyle 4\times (3^{4})+4\times (3^{5})}$
Symmetry group	${\displaystyle D_{2\mathrm {d} }}$
Dual polyhedron	Elongated gyrobifastigium
Properties	convex
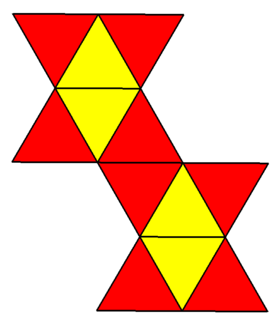
Net

In

. It can be constructed in different approaches. This shape also has alternative names called Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron; these names mean the 12-sided polyhedron.

The applications of snub disphenoid can be visualized as an

.

Construction

Involving polyhedron

The snub disphenoid can be constructed in different ways. As suggested by the name, the snub disphenoid is constructed from

The snub disphenoid may also be constructed from a triangular bipyramid, by cutting its two edges along the apices. These apices can be pushed toward each other resulting in the new two vertices pushed away.

attached with rotational symmetry.

A physical model of the snub disphenoid can be formed by folding a net formed by 12 equilateral triangles (a 12-iamond), shown. An alternative net suggested by John Montroll has fewer concave vertices on its boundary, making it more convenient for origami construction.^[4]

By Cartesian coordinates

The eight vertices of the snub disphenoid may then be given

: Here, ${\displaystyle q\approx 0.16902}$ is the positive real solution of the cubic polynomial ${\textstyle 2x^{3}+11x^{2}+4x-1.}$. The three variables ${\displaystyle r}$, ${\displaystyle s}$, and ${\displaystyle t}$ is the expression of:^[5] Because this construction involves the solution to a cubic equation, the snub disphenoid cannot be

Properties

As a consequence of such constructions, the snub disphenoid has 12 equilateral triangles. A deltahedron is a polyhedron in which all faces are equilateral triangles. There are eight convex deltahedra, one of which is the snub disphenoid.^[6] More generally, the convex polyhedron in which all faces are regular polygon are the Johnson solids, and every convex deltahedron is Johnson solid. The snub disphenoid is among them, enumerated as the 84th Johnson solid ${\displaystyle J_{84}}$.^[7]

Measurement

A snub disphenoid with edge length ${\displaystyle a}$ has a surface area:^[8]

the area of 12 equilateral triangles. Its volume can be calculated as the formula:^[8]

Symmetry and geodesic

The snub disphenoid has the same symmetries as a

${\displaystyle D_{2\mathrm {d} }}$ of order 8: it has an axis of 180° rotational symmetry through the midpoints of its two opposite edges, two perpendicular planes of reflection symmetry through this axis, and four additional symmetry operations given by a reflection perpendicular to the axis followed by a quarter-turn and possibly another reflection parallel to the axis.^[6].

Up to symmetries and parallel translation, the snub disphenoid has five types of simple (non-self-crossing) closed geodesics. These are paths on the surface of the polyhedron that avoid the vertices and locally look like the shortest path: they follow straight line segments across each face of the polyhedron that they intersect, and when they cross an edge of the polyhedron they make complementary angles on the two incident faces to the edge. Intuitively, one could stretch a rubber band around the polyhedron along this path and it would stay in place: there is no way to locally change the path and make it shorter. For example, one type of geodesic crosses the two opposite edges of the snub disphenoid at their midpoints (where the symmetry axis exits the polytope) at an angle of ${\displaystyle \pi /3}$. A second type of geodesic passes near the intersection of the snub disphenoid with the plane that perpendicularly bisects the symmetry axis (the equator of the polyhedron), crossing the edges of eight triangles at angles that alternate between ${\displaystyle \pi /2}$ and ${\displaystyle \pi /6}$. Shifting a geodesic on the surface of the polyhedron by a small amount (small enough that the shift does not cause it to cross any vertices) preserves the property of being a geodesic and preserves its length, so both of these examples have shifted versions of the same type that are less symmetrically placed. The lengths of the five simple closed geodesics on a snub disphenoid with unit-length edges are

${\displaystyle 2{\sqrt {3}}\approx 3.464}$ (for the equatorial geodesic), ${\displaystyle {\sqrt {13}}\approx 3.606}$, ${\displaystyle 4}$ (for the geodesic through the midpoints of opposite edges), ${\displaystyle 2{\sqrt {7}}\approx 5.292}$, and ${\displaystyle {\sqrt {19}}\approx 4.359}$.

Except for the tetrahedron, which has infinitely many types of simple closed geodesics, the snub disphenoid has the most types of geodesics of any deltahedron.^[9]

Representation by the graph

The snub disphenoid is

Dual polyhedron

The dual polyhedron of the snub disphenoid is the elongated gyrobifastigium. It has right-angled pentagons and can self-tessellate space.

Applications

Spheres centered at the vertices of the snub disphenoid form a cluster that, according to numerical experiments, has the minimum possible Lennard-Jones potential among all eight-sphere clusters.^[5]

In the geometry of

History and naming

This shape was called a Siamese dodecahedron in the paper by Hans Freudenthal and B. L. van der Waerden (1947) which first described the set of eight convex deltahedra.^[12]

The dodecadeltahedron name was given to the same shape by

]

The snub disphenoid name comes from

gyrobianticupola

.

References

External links

• Weisstein, Eric W. "Snub disphenoid". MathWorld.