Triaugmented triangular prism

Triaugmented triangular prism
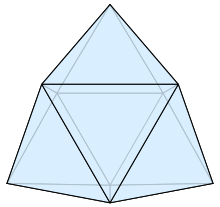Type	Deltahedron, Johnson J50 – J51 – J52
Faces	14 triangles
Edges	21
Vertices	9
Vertex configuration	${\displaystyle 3\times 3^{4}+6\times 3^{5}}$
Symmetry group	${\displaystyle D_{3\mathrm {h} }}$
Dual polyhedron	Associahedron ${\displaystyle K_{5}}$
Properties	convex
Net

The triaugmented triangular prism, in geometry, is a

The triaugmented triangular prism can be constructed by attaching

, and every convex deltahedron is a Johnson solid. The triaugmented triangular prism is numbered among the Johnson solids as ${\displaystyle J_{51}}$.

One possible system of

$${\displaystyle {\begin{aligned}\left(0,{\frac {2}{\sqrt {3}}},\pm 1\right),\qquad &\left(\pm 1,-{\frac {1}{\sqrt {3}}},\pm 1\right),\\\left(0,-{\frac {1+{\sqrt {6}}}{\sqrt {3}}},0\right),\qquad &\left(\pm {\frac {1+{\sqrt {6}}}{2}},{\frac {1+{\sqrt {6}}}{2{\sqrt {3}}}},0\right).\\\end{aligned}}}$$

Properties

A triaugmented triangular prism with edge length ${\displaystyle a}$ has surface area[9]

$${\displaystyle {\frac {7{\sqrt {3}}}{2}}a^{2}\approx 6.062a^{2},}$$

$${\displaystyle {\frac {2{\sqrt {2}}+{\sqrt {3}}}{4}}a^{3}\approx 1.140a^{3},}$$

It has the same three-dimensional symmetry group as the triangular prism, the dihedral group ${\displaystyle D_{3\mathrm {h} }}$ of order twelve. Its dihedral angles can be calculated by adding the angles of the component pyramids and prism. The prism itself has square-triangle dihedral angles ${\displaystyle \pi /2}$ and square-square angles ${\displaystyle \pi /3}$. The triangle-triangle angles on the pyramid are the same as in the

$${\displaystyle {\begin{aligned}\arccos \left(-{\frac {1}{3}}\right)&\approx 109.5^{\circ },\\{\frac {\pi }{2}}+{\frac {1}{2}}\arccos \left(-{\frac {1}{3}}\right)&\approx 144.7^{\circ },\\{\frac {\pi }{3}}+\arccos \left(-{\frac {1}{3}}\right)&\approx 169.5^{\circ }.\\\end{aligned}}}$$

Fritsch graph

The graph of the triaugmented triangular prism has 9 vertices and 21 edges. It was used by Fritsch & Fritsch (1998) as a small counterexample to Alfred Kempe's false proof of the four color theorem using Kempe chains, and its dual map was used as their book's cover illustration.^[11] Therefore, this graph has subsequently been named the Fritsch graph.^[12] An even smaller counterexample, called the Soifer graph, is obtained by removing one edge from the Fritsch graph (the bottom edge in the illustration here).^[12][13]

The Fritsch graph is one of only six connected graphs in which the

The

More generally, when a polytope is the dual of an associahedron, its boundary (a simplicial complex of triangles, tetrahedra, or higher-dimensional simplices) is called a "cluster complex". In the case of the triaugmented triangular prism, it is a cluster complex of type ${\displaystyle A_{3}}$, associated with the ${\displaystyle A_{3}}$ Dynkin diagram , the ${\displaystyle A_{3}}$ root system, and the ${\displaystyle A_{3}}$ cluster algebra.^[18] The connection with the associahedron provides a correspondence between the nine vertices of the triaugmented triangular prism and the nine diagonals of a hexagon. The edges of the triaugmented triangular prism correspond to pairs of diagonals that do not cross, and the triangular faces of the triaugmented triangular prism correspond to the triangulations of the hexagon (consisting of three non-crossing diagonals). The triangulations of other regular polygons correspond to polytopes in the same way, with dimension equal to the number of sides of the polygon minus three.^[15]

Applications

In the geometry of

In the Thomson problem, concerning the minimum-energy configuration of ${\displaystyle n}$ charged particles on a sphere, and for the Tammes problem of constructing a spherical code maximizing the smallest distance among the points, the minimum solution known for ${\displaystyle n=9}$ places the points at the vertices of a triaugmented triangular prism with non-equilateral faces, inscribed in a sphere. This configuration is proven optimal for the Tammes problem, but a rigorous solution to this instance of the Thomson problem is not known.^[20]

See also

Wikimedia Commons has media related to Triaugmented triangular prism.

• Császár polyhedron – Toroidal polyhedron with 14 triangle faces
• Steffen's polyhedron – Flexible polyhedron with 14 triangle faces

References