Boolean network: Difference between revisions

This article may require cleanup to meet Wikipedia's quality standards. No cleanup reason has been specified. Please help improve this article if you can. (August 2011) (Learn how and when to remove this message)

Part of a series on
Network science
Theory
Graph Complex network Contagion Small-world Scale-free Community structure Percolation Evolution Controllability Graph drawing Social capital Link analysis Optimization Reciprocity Closure Homophily Transitivity Preferential attachment Balance theory Network effect Social influence
Network types
Informational (computing) Telecommunication Transport Social Scientific collaboration Biological Artificial neural Interdependent Semantic Spatial Dependency Flow on-Chip
Graphs
Features Clique Component Cut Cycle Data structure Edge Loop Neighborhood Path Vertex Adjacency list / matrix Incidence list / matrix Types Bipartite Complete Directed Hyper Labeled Multi Random Weighted
Metrics Algorithms
Centrality Degree Motif Clustering Degree distribution Assortativity Distance Modularity Efficiency
Models
Topology Random graph Erdős–Rényi Barabási–Albert Bianconi–Barabási Fitness model Watts–Strogatz Exponential random (ERGM) Random geometric (RGG) Hyperbolic (HGN) Hierarchical Stochastic block Blockmodeling Maximum entropy Soft configuration LFR Benchmark Dynamics Boolean network agent based SIR
Lists Categories
Topics Software Network scientists Category:Network theory Category:Graph theory
v t e

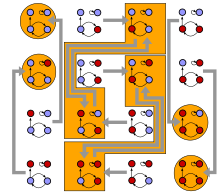
A Boolean network consists of a discrete set of

Boolean networks have been used in biology to model regulatory networks. Although Boolean networks are a crude simplification of genetic reality where genes are not simple binary switches, there are several cases where they correctly capture the correct pattern of expressed and suppressed genes.[2]^[3] The seemingly mathematical easy (synchronous) model was only fully understood in the mid 2000s.^[4]

Classical model

A Boolean network is a particular kind of

A random Boolean network (RBN) is one that is randomly selected from the set of all possible boolean networks of a particular size, N. One then can study statistically, how the expected properties of such networks depend on various statistical properties of the ensemble of all possible networks. For example, one may study how the RBN behavior changes as the average connectivity is changed.

The first Boolean networks were proposed by

Attractors

Since a Boolean network has only 2^N possible states, a trajectory will sooner or later reach a previously visited state, and thus, since the dynamics are deterministic, the trajectory will fall into a steady state or cycle called an attractor (though in the broader field of dynamical systems a cycle is only an attractor if perturbations from it lead back to it). If the attractor has only a single state it is called a point attractor, and if the attractor consists of more than one state it is called a cycle attractor. The set of states that lead to an attractor is called the basin of the attractor. States which occur only at the beginning of trajectories (no trajectories lead to them), are called garden-of-Eden states^[9] and the dynamics of the network flow from these states towards attractors. The time it takes to reach an attractor is called transient time.^[4]

With growing computer power and increasing understanding of the seemingly simple model, different authors gave different estimates for the mean number and length of the attractors, here a brief summary of key publications.^[10]

Author	Year	Mean attractor length	Mean attractor number	comment
Kauffmann [6]	1969	${\displaystyle \langle A\rangle \sim {\sqrt {N}}}$	${\displaystyle \langle \nu \rangle \sim {\sqrt {N}}}$
Bastolla/ Parisi[11]	1998	faster than a power law, ${\displaystyle \langle A\rangle >N^{x}\forall x}$	faster than a power law, ${\displaystyle \langle \nu \rangle >N^{x}\forall x}$	first numerical evidences
Bilke/ Sjunnesson[12]	2002		linear with system size, ${\displaystyle \langle \nu \rangle \sim N}$
Socolar/Kauffman[13]	2003		faster than linear, ${\displaystyle \langle \nu \rangle >N^{x}}$ with ${\displaystyle x>1}$
Samuelsson/Troein[14]	2003		superpolynomial growth, ${\displaystyle \langle \nu \rangle >N^{x}\forall x}$	mathematical proof
Mihaljev/Drossel[15]	2005	faster than a power law, ${\displaystyle \langle A\rangle >N^{x}\forall x}$	faster than a power law, ${\displaystyle \langle \nu \rangle >N^{x}\forall x}$

Stability

In dynamical systems theory, the structure and length of the attractors of a network corresponds to the dynamic phase of the network. The stability of Boolean networks depends on the connections of their

. This phenomenon is governed by a critical value of the average number of connections of nodes (${\displaystyle K_{c}}$), and can be characterized by the Hamming distance as distance measure. In the unstable regime, the distance between two initially close states on average grows exponentially in time, while in the stable regime it decreases exponentially. In this, with "initially close states" one means that the Hamming distance is small compared with the number of nodes (${\displaystyle N}$) in the network.

For N-K-model^[16] the network is stable if ${\displaystyle K<K_{c}}$, critical if ${\displaystyle K=K_{c}}$, and unstable if ${\displaystyle K>K_{c}}$.

The state of a given node ${\displaystyle n_{i}}$ is updated according to its truth table, whose outputs are randomly populated. ${\displaystyle p_{i}}$ denotes the probability of assigning an off output to a given series of input signals.

If ${\displaystyle p_{i}=p=const.}$ for every node, the transition between the stable and chaotic range depends on ${\displaystyle p}$. The critical value of the average number of connections is ${\displaystyle K_{c}=1/[2p(1-p)]}$.^[17]

If ${\displaystyle K}$ is not constant, and there is no correlation between the in-degrees and out-degrees, the conditions of stability is determined by ${\displaystyle \langle K^{in}\rangle }$^[18][19][20] The network is stable if ${\displaystyle \langle K^{in}\rangle <K_{c}}$, critical if ${\displaystyle \langle K^{in}\rangle =K_{c}}$, and unstable if ${\displaystyle \langle K^{in}\rangle >K_{c}}$.

The conditions of stability are the same in the case of networks with scale-free topology where the in-and out-degree distribution is a power-law distribution: ${\displaystyle P(K)\propto K^{-\gamma }}$, and ${\displaystyle \langle K^{in}\rangle =\langle K^{out}\rangle }$, since every out-link from a node is an in-link to another.^[21]

Sensitivity shows the probability that the output of the Boolean function of a given node changes if its input changes. For random Boolean networks, ${\displaystyle q_{i}=2p_{i}(1-p_{i})}$. In the general case, stability of the network is governed by the largest eigenvalue ${\displaystyle \lambda _{Q}}$ of matrix ${\displaystyle Q}$, where ${\displaystyle Q_{ij}=q_{i}A_{ij}}$, and ${\displaystyle A}$ is the adjacency matrix of the network.^[22] The network is stable if ${\displaystyle \lambda _{Q}<1}$, critical if ${\displaystyle \lambda _{Q}=1}$, unstable if ${\displaystyle \lambda _{Q}>1}$.

Variations of the model

Other topologies

One theme is to study different underlying

.

• The homogeneous case simply refers to a grid which is simply the reduction to the famous Ising model.
• Scale-free topologies may be chosen for Boolean networks.^[23] One can distinguish the case where only in-degree distribution in power-law distributed,^[24] or only the out-degree-distribution or both.

Other updating schemes

Classical Boolean networks (sometimes called CRBN, i.e. Classic Random Boolean Network) are synchronously updated. Motivated by the fact that genes don't usually change their state simultaneously,^[25] different alternatives have been introduced. A common classification^[26] is the following:

• Deterministic asynchronous updated Boolean networks (DRBNs) are not synchronously updated but a deterministic solution still exists. A node i will be updated when t ≡ Q_i (mod P_i) where t is the time step.^[27]
• The most general case is full stochastic updating (GARBN, general asynchronous random boolean networks). Here, one (or more) node(s) are selected at each computational step to be updated.
• The Partially-Observed Boolean Dynamical System (POBDS)^{[28][29][30][31]} signal model differs from all previous deterministic and stochastic Boolean network models by removing the assumption of direct observability of the Boolean state vector and allowing uncertainty in the observation process, addressing the scenario encountered in practice.

See also

• NK model

References

• Dubrova, E., Teslenko, M., Martinelli, A., (2005). *Kauffman Networks: Analysis and Applications, in "Proceedings of International Conference on Computer-Aided Design", pages 479-484.

External links

• DDLab
• Analysis of Dynamic Algebraic Models (ADAM) v1.1
• RBNLab
• NetBuilder Boolean Networks Simulator
• Open Source Boolean Network Simulator
• JavaScript Kauffman Network
• Probabilistic Boolean Networks (PBN)
• A SAT-based tool for computing attractors in Boolean Networks
• CoLoMoTo (Consortium for Logical Models and Tools)