Система координат

Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В

В

В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана). См. Географические координаты.

В

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.

Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел ${\displaystyle (x,y):}$

• ${\displaystyle x}$ — расстояние от точки P до оси y с учётом знака
• ${\displaystyle y}$ — расстояние от точки P до оси x с учётом знака

В пространстве необходимы уже три координаты ${\displaystyle (x,y,z):}$

• ${\displaystyle x}$ — расстояние от точки P до плоскости yz
• ${\displaystyle y}$ — расстояние от точки P до плоскости xz
• ${\displaystyle z}$ — расстояние от точки P до плоскости xy

В полярной системе координат, применяемой на плоскости, положение точки P определяется её расстоянием до начала координат r = |OP| и углом φ её радиус-вектора к оси Ox.

В пространстве применяются обобщения полярных координат — цилиндрические и сферические системы координат.

Цилиндрические координаты — трёхмерный аналог полярных, в котором точка P представляется упорядоченной тройкой ${\displaystyle (r,\varphi ,z).}$ В терминах декартовой системы координат,

• ${\displaystyle 0\leqslant {r}}$ (радиус) — расстояние от оси z до точки P,
• ${\displaystyle 0\leqslant \varphi <360^{\circ }}$ (азимут или долгота) — угол между положительной («плюсовой») частью оси x и отрезком, проведённым от полюса до точки P и спроектированной на плоскость xy.
• ${\displaystyle z}$ (высота) равна декартовой z-координате точки P.

Примечание: в литературе для первой (радиальной) координаты иногда используется обозначение ρ, для второй (угловой, или азимутальной) — обозначение θ, для третьей координаты — обозначение h.

Полярные координаты имеют один недостаток: значение φ не определено при r = 0.

Цилиндрические координаты полезны для изучения систем, симметричных относительно некоторой оси. Например, длинный цилиндр с радиусом R в декартовых координатах (с осью z, совпадающей с осью цилиндра) имеет уравнение ${\displaystyle x^{2}+y^{2}=R^{2},}$ тогда как в цилиндрических координатах оно выглядит гораздо проще, как r = R.

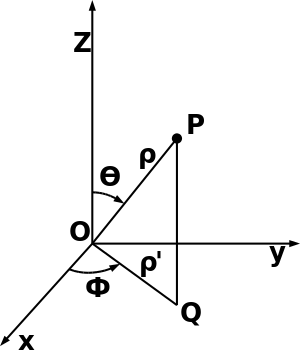
Сферические координаты — трёхмерный аналог полярных.

В сферической системе координат расположение точки P определяется тремя компонентами: ${\displaystyle (\rho ,\varphi ,\theta ).}$ В терминах декартовой системы координат,

• ${\displaystyle 0\leqslant \rho }$ (радиус) — расстояние от точки P до полюса,
• ${\displaystyle 0\leqslant \varphi \leqslant 360^{\circ }}$ (азимут или долгота) — угол между положительной («плюсовой») полуосью x и проекцией отрезка, проведённого из полюса до точки P, на плоскость xy.
• ${\displaystyle 0\leqslant \theta \leqslant 180^{\circ }}$ (широта или полярный угол) — угол между положительной («плюсовой») полуосью z и отрезком, проведённым из полюса до точки P.

Примечание: в литературе иногда азимут обозначается θ, а полярный угол - φ. Иногда для радиальной координаты используется r вместо ρ. Кроме того, диапазон углов для азимута может выбираться как (−180°, +180°] вместо диапазона [0°, +360°). Наконец, полярный угол может отсчитываться не от положительного направления оси z, а от плоскости xy; в этом случае он лежит в диапазоне [−90°, +90°], а не в диапазоне [0°, 180°]. Иногда порядок координат в тройке выбирается отличным от описанного; например, полярный и азимутальный углы могут быть переставлены.

Сферическая система координат также имеет недостаток: φ и θ не определены, если ρ = 0; угол φ не определён также и для граничных значений θ = 0 и θ = 180° (или для θ = ±90°, в случае принятия соответствующего диапазона для этого угла).

Для построения точки P по её сферическим координатам нужно от полюса вдоль положительной полуоси z отложить отрезок, равный ρ, повернуть его на угол θ вокруг оси y в направлении положительной полуоси x, и затем повернуть на угол θ вокруг оси z в направлении положительной полуоси y.

Сферические координаты полезны при изучении систем, симметричных относительно точки. Так, уравнение сферы с радиусом R в декартовых координатах с началом отсчёта в центре сферы выглядит как ${\displaystyle x^{2}+y^{2}+z^{2}=R^{2},}$ тогда как в сферических координатах оно становится намного проще: ${\displaystyle \rho =R.}$

• Аффинная (косоугольная) система координат — прямолинейная система координат в аффинном пространстве. На плоскости задается точкой начала координат О и двумя упорядоченными неколлинеарными векторами, которые представляют собой аффинный базис. Осями координат в данном случае называются прямые, проходящие через точку начала координат параллельно векторам базиса, которые, в свою очередь, задают положительное направление осей. В трехмерном пространстве, соответственно, аффинная система координат задается тройкой линейно независимых векторов и точкой начала координат. Для определения координат некоторой точки М вычисляются коэффициенты разложения вектора ОМ по векторам базиса^[1].

• однородных координат. Точка с барицентрическими координатами расположена в n-мерном векторном пространстве Eⁿ, а собственно координаты при этом относятся к фиксированной системе точек, которые не лежат в (n−1)-мерном подпространстве. Барицентрические координаты используются также и в алгебраической топологии применительно к точкам симплекса^[2]
  .