Boerdijk–Coxeter helix

Coxeter helices from regular tetrahedra

CCW and CW turning

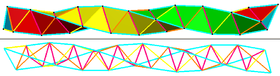Edges can be colored into 6 groups, 3 main helixes (cyan), with the concave edges forming a slow forward helix (magenta), and two backwards helixes (yellow and orange)[1]

The Boerdijk–Coxeter helix, named after

Buckminster Fuller named it a tetrahelix and considered them with regular and irregular tetrahedral elements.^[3]

Geometry

The coordinates of vertices of Boerdijk–Coxeter helix composed of tetrahedrons with unit edge length can be written in the form

${\displaystyle (r\cos n\theta ,r\sin n\theta ,nh)}$

where ${\displaystyle r=3{\sqrt {3}}/10}$, ${\displaystyle \theta =\pm \cos ^{-1}(-2/3)\approx 131.81^{\circ }}$, ${\displaystyle h=1/{\sqrt {10}}}$ and ${\displaystyle n}$ is an arbitrary integer. The two different values of ${\displaystyle \theta }$ correspond to two chiral forms. All vertices are located on the cylinder with radius ${\displaystyle r}$ along z-axis. Given how the tetrahedra alternate, this gives an apparent twist of ${\displaystyle 2\theta -{\frac {4}{3}}\pi \approx 23.62^{\circ }}$ every two tetrahedra. There is another inscribed cylinder with radius ${\displaystyle 3{\sqrt {2}}/20}$ inside the helix.^[4]

Higher-dimensional geometry

The 600-cell partitions into 20 rings of 30 tetrahedra, each a Boerdijk–Coxeter helix.^[5] When superimposed onto the 3-sphere curvature it becomes periodic, with a period of ten vertices, encompassing all 30 cells. The collective of such helices in the 600-cell represent a discrete Hopf fibration.^[6] While in 3 dimensions the edges are helices, in the imposed 3-sphere topology they are geodesics and have no torsion. They spiral around each other naturally due to the Hopf fibration.^[7] The collective of edges forms another discrete Hopf fibration of 12 rings with 10 vertices each. These correspond to rings of 10 dodecahedrons in the dual 120-cell.

In addition, the 16-cell partitions into two 8-tetrahedron rings, four edges long, and the 5-cell partitions into a single degenerate 5-tetrahedron ring.

4-polytope	Rings	Tetrahedra/ring	Cycle lengths	Net	Projection
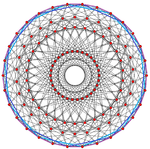
600-cell	20	30	30, 103, 152
16-cell	2	8	8, 8, 42
5-cell	1	5	(5, 5), 5

Related polyhedral helixes

Equilateral square pyramids can also be chained together as a helix, with two vertex configurations, 3.4.3.4 and 3.3.4.3.3.4. This helix exists as finite ring of 30 pyramids in a 4-dimensional polytope.

And equilateral pentagonal pyramids can be chained with 3 vertex configurations, 3.3.5, 3.5.3.5, and 3.3.3.5.3.3.5:

In architecture

The Art Tower Mito is based on a Boerdijk–Coxeter helix.

See also

• Clifford parallel cell rings
• Toroidal polyhedron
• Line group#Helical symmetry
• Skew apeirogon#Helical apeirogons in 3-dimensions

Notes

References