Mixed model

A mixed model, mixed-effects model or mixed error-component model is a

This page will discuss mainly linear mixed-effects models rather than generalized linear mixed models or nonlinear mixed-effects models.^[4]

Qualitative Description

Linear mixed models (LMMs) are

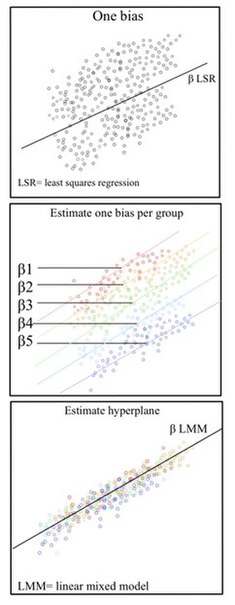
Non-independent sets are ones in which the variability between outcomes is due to correlations within groups or between groups. Mixed models properly account for nest structures/hierarchical data structures where observations are influenced by their nested associations. For example, when studying education methods involving multiple schools, there are multiple levels of variables to consider. The individual level/lower level comprises individual students or teachers within the school. The observations obtained from this student/teacher is nested within their school. For example, Student A is a unit within the School A. The next higher level is the school. At the higher level, the school contains multiple individual students and teachers. The school level influences the observations obtained from the students and teachers. For Example, School A and School B are the higher levels each with its set of Student A and Student B respectively. This represents a hierarchical data scheme. A solution to modeling hierarchical data is using linear mixed models.

LMMs allow us to understand the important effects between and within levels while incorporating the corrections for standard errors for non-independence embedded in the data structure.^[4][5]

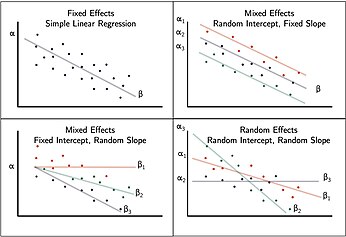
The Fixed Effect

Fixed effects encapsulate the tendencies/trends that are consistent at the levels of primary interest. These effects are considered fixed because they are non-random and assumed to be constant for the population being studied.^[5] For example, when studying education a fixed effect could represent overall school level effects that are consistent across all schools.

While the hierarchy of the data set is typically obvious, the specific fixed effects that affect the average responses for all subjects must be specified. Some fixed effect coefficients are sufficient without corresponding random effects where as other fixed coefficients only represent an average where the individual units are random. These may be determined by incorporating random

Ronald Fisher introduced random effects models to study the correlations of trait values between relatives.^[9] In the 1950s, Charles Roy Henderson provided

• ${\displaystyle {\boldsymbol {y}}}$ is a known vector of observations, with mean ${\displaystyle E({\boldsymbol {y}})=X{\boldsymbol {\beta }}}$;
• ${\displaystyle {\boldsymbol {\beta }}}$ is an unknown vector of fixed effects;
• ${\displaystyle {\boldsymbol {u}}}$ is an unknown vector of random effects, with mean ${\displaystyle E({\boldsymbol {u}})={\boldsymbol {0}}}$ and variance–covariance matrix ${\displaystyle \operatorname {var} ({\boldsymbol {u}})=G}$;
• ${\displaystyle {\boldsymbol {\epsilon }}}$ is an unknown vector of random errors, with mean ${\displaystyle E({\boldsymbol {\epsilon }})={\boldsymbol {0}}}$ and variance ${\displaystyle \operatorname {var} ({\boldsymbol {\epsilon }})=R}$;
• ${\displaystyle X}$ is the known design matrix for the fixed effects relating the observations ${\displaystyle {\boldsymbol {y}}}$ to ${\displaystyle {\boldsymbol {\beta }}}$, respectively
• ${\displaystyle Z}$ is the known design matrix for the random effects relating the observations ${\displaystyle {\boldsymbol {y}}}$ to ${\displaystyle {\boldsymbol {u}}}$, respectively.

Estimation

The joint density of ${\displaystyle {\boldsymbol {y}}}$ and ${\displaystyle {\boldsymbol {u}}}$ can be written as: ${\displaystyle f({\boldsymbol {y}},{\boldsymbol {u}})=f({\boldsymbol {y}}|{\boldsymbol {u}})\,f({\boldsymbol {u}})}$. Assuming normality, ${\displaystyle {\boldsymbol {u}}\sim {\mathcal {N}}({\boldsymbol {0}},G)}$, ${\displaystyle {\boldsymbol {\epsilon }}\sim {\mathcal {N}}({\boldsymbol {0}},R)}$ and ${\displaystyle \mathrm {Cov} ({\boldsymbol {u}},{\boldsymbol {\epsilon }})={\boldsymbol {0}}}$, and maximizing the joint density over ${\displaystyle {\boldsymbol {\beta }}}$ and ${\displaystyle {\boldsymbol {u}}}$, gives Henderson's "mixed model equations" (MME) for linear mixed models:^[10][12][17]

${\displaystyle {\begin{pmatrix}X'R^{-1}X&X'R^{-1}Z\\Z'R^{-1}X&Z'R^{-1}Z+G^{-1}\end{pmatrix}}{\begin{pmatrix}{\hat {\boldsymbol {\beta }}}\\{\hat {\boldsymbol {u}}}\end{pmatrix}}={\begin{pmatrix}X'R^{-1}{\boldsymbol {y}}\\Z'R^{-1}{\boldsymbol {y}}\end{pmatrix}}}$

The solutions to the MME, ${\displaystyle \textstyle {\hat {\boldsymbol {\beta }}}}$ and ${\displaystyle \textstyle {\hat {\boldsymbol {u}}}}$ are best linear unbiased estimates and predictors for ${\displaystyle {\boldsymbol {\beta }}}$ and ${\displaystyle {\boldsymbol {u}}}$, respectively. This is a consequence of the Gauss–Markov theorem when the conditional variance of the outcome is not scalable to the identity matrix. When the conditional variance is known, then the inverse variance weighted least squares estimate is best linear unbiased estimates. However, the conditional variance is rarely, if ever, known. So it is desirable to jointly estimate the variance and weighted parameter estimates when solving MMEs.

One method used to fit such mixed models is that of the

There are several other methods to fit mixed models, including using an MEM initially, and then Newton-Raphson (used by R package nlme^[21]'s lme()), penalized least squares to get a profiled log likelihood only depending on the (low-dimensional) variance-covariance parameters of ${\displaystyle {\boldsymbol {u}}}$, i.e., its cov matrix ${\displaystyle {\boldsymbol {G}}}$, and then modern direct optimization for that reduced objective function (used by R's lme4^[22] package lmer() and the Julia package MixedModels.jl) and direct optimization of the likelihood (used by e.g. R's glmmTMB). Notably, while the canonical form proposed by Henderson is useful for theory, many popular software packages use a different formulation for numerical computation in order to take advantage of sparse matrix methods (e.g. lme4 and MixedModels.jl).

See also

• Nonlinear mixed-effects model
• Fixed effects model
• Generalized linear mixed model
• Linear regression
• Mixed-design analysis of variance
• Multilevel model
• Random effects model
• Repeated measures design
• Empirical Bayes method

References