Portal:Mathematics

Portal topics: Activities; Culture; Geography; Health; History; Mathematics; Nature; People; Philosophy; Religion; Society; Technology; Random portal

The Mathematics Portal

social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...

)

Refresh with new selections below (purge)

Featured articles – load new batch

Featured articles
are displayed here, which represent some of the best content on English Wikipedia.

$Image 1 The number π (/paɪ/; spelled out as "pi") is a mathematical constant that is the ratio of a circle's circumference to its diameter, approximately equal to 3.14159. The number π appears in many formulae across mathematics and physics. It is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as '"`UNIQ--postMath-00000001-QINU`"' are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. For thousands of years, mathematicians have attempted to extend their understanding of π, sometimes by computing its value to a high degree of accuracy. Ancient civilizations, including the Egyptians and Babylonians, required fairly accurate approximations of π for practical computations. Around 250 BC, the Greek mathematician Archimedes created an algorithm to approximate π with arbitrary accuracy. In the 5th century AD, Chinese mathematicians approximated π to seven digits, while Indian mathematicians made a five-digit approximation, both using geometrical techniques. The first computational formula for π, based on infinite series, was discovered a millennium later. The earliest known use of the Greek letter π to represent the ratio of a circle's circumference to its diameter was by the Welsh mathematician William Jones in 1706. (Full article...)$

Image 1
The number $π$ (/paɪ/; spelled out as "pi") is a mathematical constant that is the ratio of a circle's circumference to its diameter, approximately equal to 3.14159. The number $π$ appears in many formulae across mathematics and physics. It is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as ${\tfrac {22}{7}}$ are commonly
Egyptians and Babylonians, required fairly accurate approximations of $π$ for practical computations. Around 250 BC, the Greek mathematician Archimedes created an algorithm to approximate $π$ with arbitrary accuracy. In the 5th century AD, Chinese mathematicians approximated $π$ to seven digits, while Indian mathematicians made a five-digit approximation, both using geometrical techniques. The first computational formula for $π$ , based on infinite series, was discovered a millennium later. The earliest known use of the Greek letter π to represent the ratio of a circle's circumference to its diameter was by the Welsh mathematician William Jones in 1706. (Full article...
)

Image 2

neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...
)

Image 3
Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...
)

Image 4

Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. The name of the corresponding field is actuarial science which covers rigorous mathematical calculations in areas of life expectancy and life insurance. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms.

While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design and manage programs that control risk. The actual steps needed to become an actuary are usually country-specific; however, almost all processes share a rigorous schooling or examination structure and take many years to complete. (Full article...)

$Image 5 Portrait of Kepler in 1627 Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ⓘ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium. Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein. Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. (Full article...)$

Image 5

modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. (Full article...
)

Image 6

Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...
)

$Image 7 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300). In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC). It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, they are the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)$

Image 7
fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as $252 = 21 \times 12$ and $105 = 21 \times 5)$ , and the same number 21 is also the GCD of 105 and $252 - 105 = 147$ . Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, they are the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, $21 = 5 \times 105 + (-2) \times 252$ ). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...
)

Image 8
In
rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...
)

Image 9
gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...
)

Image 10
ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.

In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history." In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics." (Full article...
)

Image 11

cryptologic bomb. (Full article...
)

Image 12

ethnographer, artist, poet, philosopher, politician, and literary scholar.

Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...
)

Image 13
positive integers, given alternating signs. Using sigma summation notation
the sum of the first m terms of the series can be expressed as
$\sum _{n=1}^{m}n(-1)^{n-1}.$

The infinite series
partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation
:
$1-2+3-4+\cdots ={\frac {1}{4}}.$ (Full article...)

Image 14

Chancellor Wang Anshi (1021–1085).

In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...
)

Image 15
proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises together with a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary
like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)

More featured articles

edit
Selected image – show another

More selected pictures

Good articles – load new batch

Good articles

, which meet a core set of high editorial standards.

Image 1
edges represent mutual acquaintance. Then a clique represents a subset of people who all know each other, and algorithms for finding cliques can be used to discover these groups of mutual friends. Along with its applications in social networks, the clique problem also has many applications in bioinformatics, and computational chemistry. (Full article...
)

Image 2
YBC 7289

YBC 7289 is a Babylonian clay tablet notable for containing an accurate sexagesimal approximation to the square root of 2, the length of the diagonal of a unit square. This number is given to the equivalent of six decimal digits, "the greatest known computational accuracy ... in the ancient world". The tablet is believed to be the work of a student in southern Mesopotamia from some time between 1800 and 1600 BC. (Full article...)
Image 3
polar coordinates
$(r,\varphi )$ by the equation
$r={\frac {a}{\varphi }},$
for an arbitrary choice of the
scale factor
$a.$ (Full article...)
Image 4
base of the natural logarithm function. It is the limit
of $(1+1/n)^{n}$ as $n$ tends to infinity, an expression that arises in the computation of compound interest. It is the value at $1$ of the (natural) exponential function, commonly denoted $e^{x}.$ It is also the sum of the infinite series
$e=\sum \limits _{n=0}^{\infty }{\frac {1}{n!}}=1+{\frac {1}{1}}+{\frac {1}{1\cdot 2}}+{\frac {1}{1\cdot 2\cdot 3}}+\cdots .$
There are various other characterizations; see § Definitions and § Representations.

The number $e$ is sometimes called Euler's number, after the Swiss mathematician Leonhard Euler, though this can invite confusion with Euler numbers, or with Euler's constant, a different constant typically denoted $\gamma$ . Alternatively, $e$ can be called Napier's constant after John Napier. The constant was discovered by the Swiss mathematician Jacob Bernoulli while studying compound interest. (Full article...)
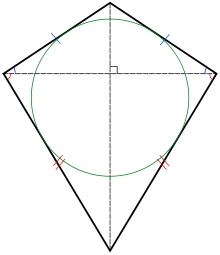
Image 5

A kite, showing its pairs of equal-length sides and its inscribed circle.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombi, with two diagonal axes of symmetry; and the squares, which are also special cases of both right kites and rhombi. (Full article...)
Image 6
clique number of certain graphs now known as Keller graphs. (Full article...
)

Image 7
16 polygonalizations of a set of six points

In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.

Every point set that does not lie on a single line has at least one polygonalization, which can be found in polynomial time. For points in convex position, there is only one, but for some other point sets there can be exponentially many. Finding an optimal polygonalization under several natural optimization criteria is a hard problem, including as a special case the travelling salesman problem. The complexity of counting all polygonalizations remains unknown. (Full article...)
Image 8
nontrivial, always have quadrisecants, and the existence and number of quadrisecants has been studied in connection with knot invariants including the minimum total curvature and the ropelength of a knot.
The number of quadrisecants of a non-singular algebraic curve in complex projective space can be computed by a formula derived by Arthur Cayley.
Quadrisecants of arrangements of skew lines touch subsets of four lines from the arrangement. They are associated with ruled surfaces and the Schläfli double six configuration.

(Full article...

)

Ashari theologians such as Al-Ghazali. Averroes argued that philosophy was permissible in Islam and even compulsory among certain elites. He also argued scriptural text should be interpreted allegorically if it appeared to contradict conclusions reached by reason and philosophy. In Islamic jurisprudence, he wrote the Bidāyat al-Mujtahid on the differences between Islamic schools of law and the principles that caused their differences. In medicine, he proposed a new theory of stroke, described the signs and symptoms of Parkinson's disease for the first time, and might have been the first to identify the retina as the part of the eye responsible for sensing light. His medical book Al-Kulliyat fi al-Tibb, translated into Latin and known as the Colliget, became a textbook in Europe for centuries. (Full article...

)

double-entry bookkeeping system. It set a new standard for writing and argumentation about algebra, and its impact upon the subsequent development and standardization of professional accounting methods was so great that Pacioli is sometimes referred to as the "father of accounting". (Full article...

)

$Image 11 Natural patterns form as wind blows sand in the dunes of the Namib Desert. The crescent shaped dunes and the ripples on their surfaces repeat wherever there are suitable conditions. Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time. In the 19th century, the Belgian physicist Joseph Plateau examined soap films, leading him to formulate the concept of a minimal surface. The German biologist and artist Ernst Haeckel painted hundreds of marine organisms to emphasise their symmetry. Scottish biologist D'Arcy Thompson pioneered the study of growth patterns in both plants and animals, showing that simple equations could explain spiral growth. In the 20th century, the British mathematician Alan Turing predicted mechanisms of morphogenesis which give rise to patterns of spots and stripes. The Hungarian biologist Aristid Lindenmayer and the French American mathematician Benoît Mandelbrot showed how the mathematics of fractals could create plant growth patterns. (Full article...)$

fractals could create plant growth patterns. (Full article...

)

scrolls. (Full article...

)

More good articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Portal:Mathematics

The Mathematics Portal

Featured articles – load new batch

Selected image – show another

Good articles – load new batch

Did you know (auto-generated) – load new batch

More did you know – view different entries

Selected article – show another

Subcategories

Topics in mathematics

Index of mathematics articles

Related portals

WikiProjects

Things you can do

In other Wikimedia projects

More portals