Поверхностное натяжение

Механика сплошных сред
Сплошная среда
Классическая механика Закон сохранения массы · Закон сохранения импульса
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Интеграл Коши — Лагранжа · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука
См. также: Портал:Физика

Пове́рхностное натяже́ние — тенденция жидкости сжиматься до минимально возможной площади поверхности. Поверхностное натяжение это то явление, которое позволяет телам с большей плотностью, чем у воды, плавать на её поверхности, при этом даже частично в неё не погрузившись (например, плавающая водомерка или монета).

Другими словами, поверхностное натяжение — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.

Поверхностное натяжение возникает на границе газообразных, жидких и твёрдых тел. Обычно под термином «поверхностное натяжение» имеется в виду поверхностное натяжение жидких тел на границе жидкость — газ. В случае жидкой поверхности раздела поверхностное натяжение правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз.

Поверхностное натяжение имеет двойной физический смысл — энергетический (термодинамический) и силовой (механический). Энергетическое (термодинамическое) определение: поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Силовое (механическое) определение: поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости^[1].

Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Коэффициент пропорциональности ${\displaystyle \gamma }$, или же ${\displaystyle \sigma }$ — сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. В СИ он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии в джоулях на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.

В 1983 году было доказано теоретически и подтверждено данными из справочников^[2], что понятие поверхностного натяжения жидкости однозначно является частью понятия внутренней энергии (хотя и специфической: для симметричных молекул близких по форме к шарообразным). Приведенные в этой журнальной статье формулы позволяют для некоторых веществ теоретически рассчитывать значения поверхностного натяжения жидкости по другим физико-химическим свойствам, например, по теплоте парообразования или по внутренней энергии^[3][4]).

В 1985 году аналогичный взгляд на физическую природу поверхностного натяжения как части внутренней энергии при решении другой физической задачи был опубликован

.

Прибор для измерения поверхностного натяжения называется тензиометр.

Из-за межмолекулярных взаимодействий, молекула находящиеся далеко от поверхности, то есть полностью окруженная другими молекулами, притягивается соседними молекулами одинаково во всех направлениях, в результате чего результирующая сила равна нулю. В свою очередь, молекулы на поверхности не имеют подобные им молекулы по всем сторонам, и поэтому они притягиваются внутрь жидкости. Это создает некоторое внутреннее давление и заставляет жидкость сжаться для достижения минимально возможной площади поверхности.^[6]

Межмолекулярная сила притяжения, действующая между молекулами одного типа называются когезия, в то время как сила, действующая между молекулами разного типа — адгезия. Равновесие между когезией и адгезией определяет степень смачивания, краевой угол смачивания и форму мениска. Когда когезия преобладает (конкретно, когда адгезия вдвое слабее когезии), смачивание происходит слабо, и мениск принимает выпуклую форму (как, например, в случае ртути и стекла). Наоборот, когда адгезия преобладает (когда когезия вдвое слабее адгезии), смачивание сильное, и мениск принимает вогнутую форму (как с водой и стеклом).

Также, на границе жидкости и воздуха существует некоторое натяжение, параллельное поверхности, которое будет противостоять внешней силе (например, вес водомерки на поверхности воды) из-за когезии между молекулами жидкости.^[6][7]

Поверхность жидкости обладает свободной энергией:

${\displaystyle {\mathcal {E}}_{surf}=\sigma S,}$

где ${\displaystyle \sigma }$ — коэффициент поверхностного натяжения,

${\displaystyle S}$ — полная площадь поверхности жидкости^[8].

Так как свободная энергия изолированной системы стремится к минимуму, то жидкость (в отсутствие внешних полей) стремится принять форму, имеющую минимальную площадь поверхности. Таким образом задача о форме жидкости сводится к

, однако при более сложных начальных условиях задача о форме поверхности жидкости становится математически исключительно сложной.

Рассмотрим тонкую жидкую плёнку, толщиной которой можно пренебречь. Стремясь минимизировать свою свободную энергию, плёнка создаёт разность давления с разных сторон. Этим объясняется образование

в этой точке и задаётся формулой Лапласа:

${\displaystyle \Delta p=\sigma K=\sigma \left({1 \over R_{1}}+{1 \over R_{2}}\right).}$

Здесь ${\displaystyle R_{1,2}}$ — радиусы

в точке, и разный знак — если по разную сторону. Например, для сферы центры кривизны в любой точке поверхности совпадают с центром сферы, поэтому:

${\displaystyle R_{1}=R_{2}=R,}$

${\displaystyle \Delta p={2\sigma \over R}.}$

Для случая поверхности кругового цилиндра радиуса ${\displaystyle R}$ имеем:

${\displaystyle R_{1}=R,~~~R_{2}=\infty ,}$

${\displaystyle \Delta p={\sigma \over R}.}$

Так как ${\displaystyle \Delta p}$ должна быть непрерывной функцией на поверхности плёнки, поэтому выбор «положительной» стороны плёнки в одной точке локально однозначно задаёт положительную сторону поверхности в достаточно близких её точках.

Из формулы Лапласа следует, что свободная мыльная плёнка, натянутая на рамку произвольной формы и не образующая пузырей, будет иметь среднюю кривизну, равную 0.

Так как увеличение площади поверхности раздела жидкость — газ требует совершения работы, жидкость «стремится» уменьшить площадь своей поверхности:

• в невесомости порция жидкости принимает сферическую форму (сфера имеет наименьшую площадь поверхности среди всех тел одинакового объёма). То же самое происходит с каплей жидкости, помещаемой внутрь другой жидкости с такой же плотностью, при условии, что обе жидкости не смешиваются между собой. (опыт Плато).
• ламинарная струя воды образует цилиндр, который затем разбивается на шаровидные капли из-за неустойчивости Рэлея — Плато.
• небольшие предметы со средней плотностью большей плотности жидкости способны «плавать» на поверхности жидкости, так как их вес оказывается уравновешенным силой поверхностного натяжения.
• некоторые насекомые (например, водомерки) способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения.
• На многих поверхностях, именуемых несмачиваемыми (гидрофобными), вода (или другая жидкость) собирается в капли.
• Поплавок Ван Дер Месбрюгге - поплавок, имеющий кольцо. Если нажать на поплавок, то он будет удерживаться в нажатом состоянии благодаря силам поверхностного натяжения, они действуют на кольцо, и в свою очередь уравновешивают гидростатические силы, стремящиеся вытолкнуть поплавок из воды.
• Слёзы вина — образование капель и ручейков на стенках стакана, содержащего алкогольный напиток (например, вино). Причина этого явления — сложное взаимодействие между различными значениями поверхностного натяжения у воды и спирта.

• 
  Лавовая лампа работает из-за взаимодействия двух несмешивающихся жидкостей: воды и жидкого воска
• 
  Поток воды из крана разбивается на мелкие капли
• 
  Водомерка на поверхности воды
• 
  Капля воды на листе
• 
  На фотографии виден эффект, получивший название «слёзы вина»
• 
  Маргаритка. Поверхностное натяжение не дает воде затечь внутрь цветка.
• 
  Мыльный пузырь, уравновешивающий силы поверхностного натяжения и внутреннего давления
• 
  Вода набегает на сухую поверхность асфальта

Поверхностное натяжение имеет два способа определения: силовой (механический), и энергетический (термодинамический).

Эквивалентность данных двух определений может быть доказана с помощью анализа размерности.^[9]

Поверхностное натяжение ${\displaystyle \sigma }$ — сила на единицу длины. На иллюстрации справа, прямоугольная рамка, состоящая из трех неподвижных сторон (на картинке чёрные), которые образуют U-образную форму, и четвёртую (синяя), подвижную сторону, которая может двигаться направо. Поверхностное натяжение будет тянуть синюю сторону влево. Сила F, необходимая, чтобы удерживать подвижную сторону на месте, пропорциональная длине L неподвижной стороны. Таким образом, отношение ${\displaystyle {\frac {F}{L}}}$ зависит только от внутренних свойств жидкости (таких как состав, температура и так далее), но не от её формы. Таким образом, значение данного отношения оказывается одинаковым для всех форм. Отсюда, поверхностное натяжение можно определить как

${\displaystyle \sigma ={\frac {F}{2L}}.}$

Так как плёнка имеет две стороны, каждая из которых одинаково влияет на затрачиваемую силу, в формуле появляется коэффициент ${\displaystyle {\frac {1}{2}}.}$ Таким образом, влияние одной стороны плёнки равно ${\displaystyle \sigma L={\frac {F}{2}}.}$

Поверхностное натяжение ${\displaystyle \sigma }$ жидкости — отношение изменения в энергии жидкости к изменению в площади поверхности жидкости (которое и приводит к изменению в энергии). Данное определение можно связать с предыдущим^[10]: если сила F это сила, требуемая для того, что бы не допустить начало движения стороны, тогда это также и сила, которая будет удерживать подвижную сторону в состоянии движения с постоянной скоростью (по второму закону Ньютона). Но если сторона движется вправо, площадь поверхности жидкости увеличивается по мере того, как эта сила прикладывает работу к жидкости. Это означает, что с увеличением площади поверхности, также увеличивается энергия плёнки. Работа A, выполненная силой F, для передвижения подвижной стороны на дистанцию Δx равна A = FΔx. В то же время, площадь плёнки увеличится на ΔS = 2LΔx (опять же, коэффициент 2 потому, что плёнка имеет 2 стороны). Таким образом, умножая и числитель, и знаменатель ${\displaystyle \sigma ={\frac {F}{2L}}}$ на Δx получаем${\displaystyle \sigma ={\frac {F}{2L}}={\frac {F\Delta x}{2L\Delta x}}={\frac {A}{\Delta S}}.}$

Данная работа A обычно интерпретируется как запасённая в виде потенциальной энергии. Следовательно, поверхностное натяжение может быть измерено в системе СИ как джоуль на квадратный метр, или в СГС как эрг на квадратный сантиметр.

Так как механические системы всегда пытаются находится в состоянии минимальной потенциальной энергии, свободные капли жидкости естественным образом принимают сферическую форму, которая имеет минимально возможную площадь для заданного объема.

Поверхность любой жидкости фактически является границей между этой жидкостью и какой-либо другой средой. Например, поверхность лужи это граница между водой и воздухом. Отсюда, поверхностное натяжение это не просто свойство жидкости, но свойство границы жидкости с другой средой.

Если жидкость находится в сосуде, тогда помимо границы жидкость-воздух, также существует граница между жидкостью и стенками сосуда. Обычно, поверхностное натяжение между жидкостью и воздухом отличается (сильнее) от поверхностного натяжения между жидкостью и стенками. Там, где две поверхности встречаются, их форма должна быть такой, что бы все силы были уравновешены.^[9][11]

Там, где две поверхности встречаются, они образуют краевой угол смачивания θ, который является углом, который касательная к поверхности образует с твёрдой поверхностью. Важно заметить, что этот угол отсчитывается сквозь жидкость (см. иллюстрацию).

Индексы сил обозначают, к какой границе они относятся. Например, F_la обозначает силу, относящуюся к границе жидкость-воздух (от англ. l — liquid — жидкость, a — air — воздух, s — solid — твёрдое тело).

Иллюстрация справа показывает два случая.

В случае слева, разность между поверхностным натяжением границ жидкость-стенка и стенка-воздух меньше, чем натяжение на границе жидкость воздух , но в то же время больше, чем ноль. То есть

${\displaystyle \sigma _{\mathrm {la} }>\sigma _{\mathrm {ls} }-\sigma _{\mathrm {sa} }>0}$

На иллюстрации, и вертикальные, и горизонтальные компоненты сил должны нейтрализовать друг друга именно в точке контакта, что известно как равновесие. Горизонтальный компонент силы f_la нейтрализуется адгезивной силой f_A.

${\displaystyle f_{\mathrm {A} }=f_{\mathrm {la} }\sin \theta }$

Однако, с вертикальными компонентами сил ситуация слегка сложнее. Вертикальный компонент f_la должен точно нейтрализовать разницу сил вдоль стенок сосуда f_ls − f_sa.

${\displaystyle f_{\mathrm {ls} }-f_{\mathrm {sa} }=-f_{\mathrm {la} }\cos \theta }$

Так как эти силы прямо пропорциональны их соответственным поверхностным натяжениям, получается выражение^[11]

${\displaystyle \sigma _{\mathrm {ls} }-\sigma _{\mathrm {sa} }=-\sigma _{\mathrm {la} }\cos \theta }$

где краевой угол θ меньше 90° в вогнутом мениске, и больше 90° в выпуклом.^[9]

Это значит, что хотя разницу между поверхностным натяжением на границе жидкость-стенка и стенка-воздух ${\displaystyle \sigma _{\mathrm {ls} }-\sigma _{\mathrm {sa} }}$ достаточно тяжело измерить, её значение можно вывести из натяжения границы жидкость-воздух ${\displaystyle \sigma _{\mathrm {la} }}$ и краевого угла θ (см. основную статью краевой угол смачивания).

То же отношение существует и для случая справа. Но в этом случае, краевой угол меньше 90°, и из-за этого разница поверхностных натяжений на границе жидкость-стенка и стенка-воздух должна быть отрицательной. Отсюда

${\displaystyle \sigma _{\mathrm {la} }>0>\sigma _{\mathrm {ls} }-\sigma _{\mathrm {sa} }}$

Когда тело помещено на поверхность жидкости, его вес продавливает поверхность. Если тело плавает на поверхности, значит его вес становится уравновешен силами поверхностного натяжения , которые действуют параллельно участку, где происходит контакт тела с поверхностью. В таком случае, даже слабое движение тела может заставить его утонуть. Горизонтальные составляющие F_s нейтрализуют друг друга, в то время как вертикальные складываются и становятся равны весу тела F_w . Для того, что бы тело не тонуло, его поверхность не должна быть смачиваемой жидкостью. Также, вес тела должен быть достаточно невелик, для того что бы поверхностное натяжение могло протистоять ему. В итоге, получается выражение, где m — масса тела, и g — ускорение свободного падения

${\displaystyle F_{\mathrm {w} }=2F_{\mathrm {s} }\sin \theta \quad \Leftrightarrow \quad mg=2\sigma L\sin \theta }$

Старомодный ртутный барометр состоит из вертикальной стеклянной трубки с диаметром около 1 см, частично наполненной ртутью и вакуумом (известным как вакуум Торричелли). Уровень ртути в центре трубки выше, чем по у стенок, из-за чего поверхность ртути становится выпуклой. Центр масс всего столба ртути будет слегка ниже, если поверхность ртути в трубке будет плоской. Но при этом, из-за выпуклой формы поверхности, вся масса ртути имеет слегка меньшую площадь поверхности. Опять, сочетание обеих сил приводит к уменьшению общей потенциальной энергии. В этом случае, поверхность ртути образует выпуклый мениск.

В данном случае, учитывается площадь поверхности всей массы ртути, учитывая ту часть, которая находится в контакте со стеклом, поскольку ртуть совсем не смачивает стекло. Таким образом, поверхностное натяжение ртути действует по всей площади поверхности, включая ту часть, которая касается стекла.

Если же вместо стекла будет, например, медь, ситуация сильно изменится. Ртуть очень сильно смачивает медь. Поэтому, уровень ртути в медной трубке будет ниже в центре, и выше у стенок. В этом случае, ртуть образует вогнутый мениск

В случае, когда жидкость смачивает стенки сосуда, можно сказать, что поверхностное натяжение на границе жидкости и стенок отрицательное. Таким образом, жидкость пытается увеличить площадь поверхности. Поэтому, в случае меди и ртути, увеличение в площади поверхности скорее уменьшает, чем увеличивает, потенциальную энергию.

Если сосуд достаточно узкий, и жидкость достаточно сильно смачивает стенки, жидкость внутри сосуда может подняться на значительную высоту. Данное явление называется капиллярность. Высота, на которую может подняться жидкость, описывается формулой Жюрена (см. капиллярность).

При проливании ртути на горизонтальный участок стекла, образуется лужа, которая имеет вполне заметную высоту. Лужа будет растекаться только до того момента, пока ее высота не будет равняться около половины сантиметра, не меньше. Опять, данное явление происходит из-за сильного поверхностного натяжения ртути. Из-за массы жидкости, ртуть стремится опустится как можно ниже, из-за чего увеличивается площадь поверхности. Однако, поверхностное натяжение действует наоборот, пытаясь уменьшить площадь поверхности. В результате равновесия, получается практически постоянная высота лужи.

Такая же демонстрация поверхностного натяжения может быть проведена и с водой, но только на поверхности, которую вода не смачивает (например, воск). Вода, пролитая на горизонтальную поверхность, покрытую воском, будет вести себя подобно ртути на стекле.

Высота лужи жидкости на поверхности, где краевой угол смачивания равен 180° (то есть жидкость совсем не смачивает поверхность) описывается следующей формулой^[11]

${\displaystyle h=2{\sqrt {\frac {\sigma }{g\rho }}}}$

где

• h — высота лужи
• ${\displaystyle \sigma }$ — коэффициент поверхностного натяжения жидкости
• g — ускорение свободного падения
• ρ — плотность жидкости.

На самом деле, в большинстве случаев, высота лужи будет слегка меньше, чем предсказывает формула, поскольку лишь некоторые поверхности имеют краевой угол 180° с какой-либо жидкостью. В случае, когда краевой угол меньше 180°, высота равна

${\displaystyle h={\sqrt {\frac {2\sigma \left(1-\cos \theta \right)}{g\rho }}}.}$

К примеру, высота ртути на стекле примерна равна h_Hg = 0,36 см. Вода на парафине — h_H2O = 0,44 см.

Также, исходя из формулы можно обнаружить, что в случае, когда краевой угол равен 0°, жидкость растечётся очень тонким слоем по всей поверхности. Такая поверхность является полностью смачиваемой жидкостью.

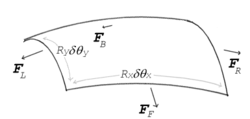
Если на натянутую поверхность не действует ни одна сила, перпендикулярная поверхности, поверхность должна оставаться плоской. Но если давление с одной стороны поверхности отличается от давления с другой, разница в давлении, умноженная на площадь поверхности, выступает как эта самая сила. Для того, что бы силе поверхностного натяжения противостоять силе, вызванную разницей давлений, поверхность должна быть искривлена. Иллюстрация справа показывает, как кривизна поверхности ведет к образованию сил, результирующий компонент которых в итоге оказываются перпендикулярен центру участка поверхности. Когда все силы уравновешены, получившееся уравнение известно как уравнение Юнга — Лапласа (или же Закон Лапласа)

${\displaystyle \Delta p=\sigma \left({\frac {1}{R_{x}}}+{\frac {1}{R_{y}}}\right)}$

где

• Δp — разница давлений, известная как давление Лапласа.^[12]
• ${\displaystyle \sigma }$ — коэффициент поверхностного натяжения.
• R_x и R_y — радиусы кривизны в каждой координате, которые параллельны поверхности.

Решение этого уравнения определяет форму капель воды, луж, менисков, мыльных пузырей, и всех остальных форм, определяемых поверхностным натяжением (таких как форма отпечатков, которые оставляют лапы водомерки на поверхности воды).

Таблица ниже показывает, как внутреннее давление капли воды при стандартных условиях увеличивается вместе с уменьшением радиуса.

Радиус капли	1 мм	м	1 мкм	10 нм
Δp (атм)	0.0014	0.0144	1.436	143.6

При не слишком маленьких размерах капли эффект незначительный. Но разность в давлениях становится огромной, когда размеры капли достигают молекулярных размеров. (В случае единственной молекулы, данный принцип становится бессмысленным.)

Непрерывный поток воды, например, из водопроводного крана, всегда разбивается на мелкие капли, не зависимо от того, насколько гладким и устойчивым он казался изначально. Это происходит из-за явления, названного неустойчивость Рэлея — Плато, которое является целиком и полностью следствием эффектов поверхностного натяжения.

Объяснение этого явления начинается с существования незначительных возмущений в потоке жидкости. Данные возмущения присутствуют в любом потоке жидкости, независимо от его свойств. Если разбить эти возмущения на синусоидные компоненты, можно обнаружить, что некоторые из них увеличиваются со временем, а другие наоборот — ослабевают. Через некоторое время, эти возмущения усилятся настолько, что в одних местах они будут сжимать поток, а в других — расширять. Это будет продолжаться до тех пор, пока поток окончательно не разобьется на отдельные сферы.

Также, здесь можно применить принцип наименьшей потенциальной энергии. Множество отдельных сфер имеют меньшую площадь поверхности, чем единый цилиндрический поток, при одинаковом объеме, и, соответственно, имеют в общем меньшую потенциальную энергию.

С увеличением температуры величина поверхностного натяжения уменьшается и равна нулю при критической температуре. Наиболее известная эмпирическая зависимость поверхностного натяжения от температуры была предложена Лорандом Этвёшом, так называемое правило Этвёша. В настоящее время получен вывод теоретической зависимости поверхностного натяжения от температуры в области до критических температур, подтверждающей правило Этвёша^[13].

Методы измерения поверхностного натяжения делятся на статические и динамические. В статических методах поверхностное натяжение определяется у сформировавшейся поверхности, находящейся в равновесии. Динамические методы связаны с разрушением поверхностного слоя. В случае измерения поверхностного натяжения растворов (особенно полимеров или ПАВ) следует пользоваться статическими методами. В ряде случаев равновесие на поверхности может наступать в течение нескольких часов (например, в случае концентрированных растворов полимеров с высокой вязкостью). Динамические методы могут быть применены для определения равновесного поверхностного натяжения и динамического поверхностного натяжения. Например, для раствора мыла после перемешивания поверхностное натяжение 58 мДж/м², а после отстаивания — 35 мДж/м². То есть поверхностное натяжение меняется. До установления равновесного оно будет динамическое.

Статические методы:

1. Метод измерения высоты поднятия мениска в капилляре.
2. Метод Вильгельми.
3. Метод лежачей капли.
4. Метод определения по форме висячей капли.
5. Метод вращающейся капли.

Динамические методы:

1. Метод дю Нуи (метод отрыва кольца).
2. Сталагмометрический, или метод счета капель.
3. Метод максимального давления пузырька.
4. Метод осциллирующей струи.
5. Метод стоячих волн.
6. Метод бегущих волн.

Полностью стандартизованные методы измерений описываются в соответствующих

и т. д.

Сущностью метода является измерение диаметра капли жидкости, вращающейся в более тяжелой жидкости

свойств.

Метод Дю Нуи (метод отрыва кольца)

Метод является классическим. Сущность метода вытекает из названия. Кольцо из платиновой проволоки плоскость которого параллельна поверхности жидкости медленно поднимают из жидкости, смачивающей его, усилие в момент отрыва кольца от поверхности и есть сила поверхностного натяжения и может быть пересчитано в поверхностную энергию. Метод подходит для измерения поверхностного натяжения ПАВ, трансформаторных масел и т. д.

При возмущении жидкости колеблющейся пластиной, лежащей на её поверхности, по поверхности жидкости распространяются

. Если осветить кювету с жидкостью импульсным источником света (стробоскопом) с частотой вспышек равной частоте колебания пластины возмущения, то будет наблюдаться зрительно неподвижная волновая картина. По измеренной длине волны можно рассчитать величину поверхностного натяжения по формуле:

${\displaystyle \sigma ={\frac {\rho \lambda ^{2}}{4\pi ^{2}}}(2\pi \nu ^{2}\lambda -g),}$

где ${\displaystyle \sigma }$ — поверхностное натяжение;

${\displaystyle \rho }$ — плотность жидкости;

${\displaystyle \lambda }$ — длина волны;

${\displaystyle \nu }$ — частота колебания пластины;

${\displaystyle g}$ — ускорение свободного падения.

Вещество	Температура °C	Поверхностное натяжение(10−3 Н/м)
Хлорид натрия 6 M водный раствор	20	82,55
Хлорид натрия	801	115
Глицерин	30	64,7
Олово	400	518
Азотная кислота 70 %	20	59,4
Анилин	20	42,9
Ацетон	20	23,7
Бензол	20	29,0
Вода	20	72,86
Глицерин	20	59,4
Нефть	20	26
Ртуть	20	486,5
Серная кислота 85 %	20	57,4
Спирт этиловый	20	22,8
Уксусная кислота	20	27,8
Эфир этиловый	20	16,9
Раствор мыла	20	43

Внешние видеофайлы
	Видео, демонстрирующее передвижение водомерки по поверхности воды за счёт поверхностного натяжения.

• Тензиометр
• Формула Жюрена

• [www.xumuk.ru/colloidchem/19.html Методы определения поверхностного натяжения]
• Видео о физической природе поверхностного натяжения жидкости как части внутренней энергии Архивная копия от 20 декабря 2020 на Wayback Machine (рус.)

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок www.xumuk.ru