Разность множеств

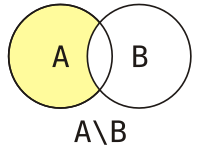
Ра́зность двух мно́жеств — теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно разность множеств ${\displaystyle A}$ и ${\displaystyle B}$ обозначается как ${\displaystyle A\setminus B}$, но иногда можно встретить обозначение ${\displaystyle A-B}$ и ${\displaystyle A\sim B}$.

Пусть ${\displaystyle A}$ и ${\displaystyle B}$ — два указанных в определении множества, тогда их разность определяется (на теоретико-множественном языке):

${\displaystyle A\setminus B=\{x\in A\mid x\not \in B\}.}$

Когда ${\displaystyle A\subseteq B}$, множество ${\displaystyle B\setminus A}$ часто называют дополнением множества ${\displaystyle A}$ до множества ${\displaystyle B}$.

Обычно предполагается, что рассматриваются подмножества одного и того же множества, которое, в этом случае называют универсумом, скажем, ${\displaystyle X}$. Тогда можно рассматривать вместе с каждым множеством ${\displaystyle A\subset X}$ и его дополнение до множества ${\displaystyle X}$ — множество ${\displaystyle X\setminus A}$, при обозначении которого часто опускается значок универсума: ${\displaystyle \setminus A}$^{[источник не указан 3230 дней]}; при этом говорится, что ${\displaystyle \setminus A}$ — (просто) дополнение множества (без указания, дополнением до чего является данное множество).

С учётом данного замечания, оказывается, что ${\displaystyle A\setminus B=A\cap (\setminus B)}$, то есть дополнение множества ${\displaystyle B}$ до множества ${\displaystyle A}$ есть пересечение множества ${\displaystyle A}$ и дополнения множества ${\displaystyle B}$.

Также применяется и операторная запись вида ${\displaystyle A^{\complement }}$, ${\displaystyle \complement _{X}A}$ или (если опустить универсальное множество) ${\displaystyle \complement A}$, ${\displaystyle {\overline {A}}}$, ${\displaystyle A'}$.

Операция разности множеств не является по определению симметричной по отношению ко входящим в неё множествам. Симметричный вариант теоретико-множественной разности двух множеств описывается понятием симметрической разности.

• Пусть ${\displaystyle A=\{3,\;4,\;5,\;6\},\;B=\{6,\;7,\;8,\;9,\;10\}}$. Тогда ${\displaystyle A\setminus B=\{3,\;4,\;5\},\;B\setminus A=\{7,\;8,\;9,\;10\}.}$
• Пусть ${\displaystyle \mathbb {R} }$ — множество всех вещественных чисел, ${\displaystyle \mathbb {Q} }$ — множество рациональных чисел, а ${\displaystyle \mathbb {Z} }$ — множество целых чисел. Тогда ${\displaystyle \mathbb {R} \setminus \mathbb {Q} }$ — множество всех иррациональных чисел, а ${\displaystyle \mathbb {Q} \setminus \mathbb {Z} }$ — дробных.

Пусть ${\displaystyle A,\;B,\;C,\;D}$ — произвольные множества.

• Вычитание множества из самого себя даёт в результате пустое множество:

${\displaystyle A\setminus A=\varnothing .}$

• Свойства пустого множества относительно разности:

${\displaystyle \varnothing \setminus A=\varnothing ;}$

${\displaystyle A\setminus \varnothing =A.}$

• Разность двух множеств содержится в уменьшаемом:

${\displaystyle A\setminus B\subset A.}$

• ${\displaystyle A\cup (B\setminus A)=A\cup B}$. Из этой формулы следует, что операция разности не является обратной операции суммы (то есть объединению).
• ${\displaystyle A\setminus B=A\setminus (A\cap B).}$
• Разность не пересекается с вычитаемым:

${\displaystyle A\cap (B\setminus A)=\varnothing .}$

• Разность множеств равна пустому множеству тогда и только тогда, когда уменьшаемое содержится в вычитаемом:

${\displaystyle A\setminus B=\varnothing \Leftrightarrow A\subset B.}$

• Законы де Моргана в алгебре множеств формулируются следующим образом:

${\displaystyle A\setminus (B\cap C)=(A\setminus B)\cup (A\setminus C);}$

${\displaystyle A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C).}$

• ${\displaystyle (A\cup B)\setminus C=(A\setminus C)\cup (B\setminus C);}$
• ${\displaystyle A\setminus (B\setminus C)=(A\setminus B)\cup (A\cap C);}$
• ${\displaystyle A\setminus (B\cup C)=(A\setminus B)\setminus C;}$
• ${\displaystyle (B\setminus A)\cap C=(B\cap C)\setminus A=B\cap (C\setminus A);}$
• ${\displaystyle (B\setminus A)\cup C=(B\cup C)\setminus A}$, если ${\displaystyle C\cap A=\varnothing }$.
• Если ${\displaystyle A\subset B}$ и ${\displaystyle C\subset D}$, то ${\displaystyle (A\setminus D)\subset (B\setminus C);}$
• Если ${\displaystyle A\subset B}$, то для любого ${\displaystyle C}$ выполняется ${\displaystyle (C\setminus B)\subset (C\setminus A)}$. Это соотношение имеет свой аналог в арифметике: если ${\displaystyle a\leqslant b}$, то для любого ${\displaystyle c}$ справедливо ${\displaystyle (c-b)\leqslant (c-a)}$.

В пакете Mathematica операция реализована с помощью функции Complement. В пакете MATLAB она же реализована с помощью функции setdiff.

В языке программирования

В языке программирования Python операция реализована с помощью метода diff над объектом типа set.

Если из контекста следует, что все рассматриваемые множества являются

${\displaystyle X}$

${\displaystyle A^{\complement }=X\setminus A\equiv \{x\in X\mid x\not \in A\}.}$

• Операция дополнения является
  булеане
  ${\displaystyle 2^{X}}$.
• Законы дополнения:^[1]

• ${\displaystyle A\cup A^{\complement }=X;}$
• ${\displaystyle A\cap A^{\complement }=\varnothing .}$

В частности, если оба ${\displaystyle A}$ и ${\displaystyle A^{\complement }}$ непусты, то ${\displaystyle \{A,\;A^{\complement }\}}$ является разбиением ${\displaystyle X}$.

• ${\displaystyle X^{\complement }=\varnothing ;}$
• ${\displaystyle \varnothing ^{\complement }=X;}$
• ${\displaystyle (A\subset B)\Leftrightarrow (B^{\complement }\subset A^{\complement }).}$

• Операция дополнения является инволюцией:

${\displaystyle (A^{\complement })^{\complement }=A.}$

• Законы де Моргана:

• ${\displaystyle (A\cup B)^{\complement }=A^{\complement }\cap B^{\complement };}$
• ${\displaystyle (A\cap B)^{\complement }=A^{\complement }\cup B^{\complement }.}$

• Законы разности множеств:

• ${\displaystyle A\setminus B=A\cap B^{\complement };}$
• ${\displaystyle (A\setminus B)^{\complement }=A^{\complement }\cup B.}$

• Операции над множествами

• Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. — М.: Физматлит, 2004. — 256 с.
• Куратовский К., Мостовский А. Теория множеств / Пер. с англ. М. И. Кратко, под ред. А. Д. Тайманова. — М.: Мир, 1970. — С. 16
  , 20—22.