Число пересечений (теория узлов)

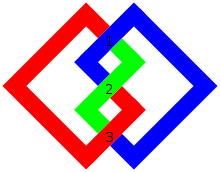
В теории узлов число пересечений узла — это наименьшее число пересечений на любой диаграмме узла. Число пересечений является инвариантом узла.

В качестве примера: тривиальный узел имеет нулевое число пересечений, число пересечений трилистника равно трём, а число пересечений восьмёрки равно четырём. Больше нет узлов с числом пересечений четыре и меньше, и есть только два узла с числом пересечений пять, но число узлов с конкретными числами пересечений быстро растёт по мере роста числа пересечений.

Таблицы

Имеется очень малый прогресс в понимании поведения числа пересечений при элементарных операциях на узлах. Большой открытый вопрос — является ли число пересечений аддитивной по отношению к операции конкатенации. Также ожидается, что сателлитный узел узла K будет иметь большее число пересечений, чем K, но это не доказано.

Аддитивность числа пересечений конкатенации узлов доказана для специальных случаев, например, если исходные узлы являются альтернированными^[2] или если исходные узлы являются торическими^[3][4]. Марк Лакенбай дал доказательство, что существует константа N > 1, такая что ${\displaystyle {\frac {1}{N}}(\mathrm {cr} (K_{1})+\mathrm {cr} (K_{2}))\leq \mathrm {cr} (K_{1}+K_{2})}$, но его метод, использующий нормальные поверхности^[англ.], не может улучшить N до 1^[5].

Имеется странная связь между числом пересечений узла и физическим поведением узлов ДНК. Для простых узлов ДНК число пересечений является хорошим предсказателем относительной скорости узла ДНК электрофореза геля агарозы. В основном, более высокое число пересечений приводит к большей относительной скорости^[6].

Имеются связанные понятия среднего числа пересечений^[англ.] и асимптотического числа пересечений. Оба этих понятия определяют границы стандартного числа пересечений. Есть гипотеза, что асимптотическое число пересечений равно числу пересечений.

Другие числовые инварианты узла включают

• Simon Jonathan. Energy functions for knots: Beginning to predict physical behavior // Mathematical Approaches to Biomolecular Structure and Dynamics / Jill P. Mesirov, Klaus Schulten, De Witt Sumners. — 1996. — Т. 82. — (The IMA Volumes in Mathematics and its Applications). —
  doi:10.1007/978-1-4612-4066-2_4
  .
• P. G. Tait. On Knots I, II, III // Scientific papers. — Cambridge University Press, 1898. — Т. 1.
• C. A. Adams. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. — American Mathematical Society, 2004. — ISBN 9780821836781.
• H. Gruber. Estimates for the minimal crossing number. — 2003. — arXiv:math/0303273.
• Yuanan Diao. The additivity of crossing numbers // Journal of Knot Theory and its Ramifications. — 2004. — Т. 13, вып. 7. —
  doi:10.1142/S0218216504003524
  .
• Marc Lackenby. The crossing number of composite knots // Journal of Topology. — 2009. — Т. 2, вып. 4. —
  doi:10.1112/jtopol/jtp028
  .

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки.