Kaluza–Klein theory

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: "Kaluza–Klein theory" – news · newspapers · books · scholar · JSTOR (January 2023) (Learn how and when to remove this message)

Beyond the Standard Model
Simulated Large Hadron Collider CMS particle detector data depicting a Higgs boson produced by colliding protons decaying into hadron jets and electrons
Standard Model
Evidence Hierarchy problem Dark matter Dark energy Quintessence Phantom energy Dark radiation Dark photon Cosmological constant problem Strong CP problem Neutrino oscillation
Theories Brans–Dicke theory Cosmic censorship hypothesis Fifth force F-theory Theory of everything Unified field theory Grand Unified Theory Technicolor Kaluza–Klein theory 6D (2,0) superconformal field theory Noncommutative quantum field theory Quantum cosmology Brane cosmology String theory Superstring theory M-theory Mathematical universe hypothesis Mirror matter Randall–Sundrum model N = 4 supersymmetric Yang–Mills theory Twistor string theory Dark fluid Doubly special relativity de Sitter invariant special relativity Causal fermion systems Black hole thermodynamics Unparticle physics Graviphoton Graviscalar Graviton Gravitino Massive gravity Gauge gravitation theory Gauge theory gravity CPT symmetry
Supersymmetry MSSM NMSSM Superstring theory M-theory Supergravity Supersymmetry breaking Extra dimensions Large extra dimensions
Quantum gravity False vacuum String theory Spin foam Quantum foam Quantum geometry Loop quantum gravity Quantum cosmology Loop quantum cosmology Causal dynamical triangulation Causal fermion systems Causal sets Canonical quantum gravity Semiclassical gravity Superfluid vacuum theory
Experiments ANNIE Gran Sasso INO LHC SNO Super-K Tevatron NOvA
v t e

In

The five-dimensional (5D) theory developed in three steps. The original hypothesis came from

, and an equation for the scalar field. Kaluza also introduced the "cylinder condition" hypothesis, that no component of the five-dimensional metric depends on the fifth dimension. Without this restriction, terms are introduced that involve derivatives of the fields with respect to the fifth coordinate, and this extra degree of freedom makes the mathematics of the fully variable 5D relativity enormously complex. Standard 4D physics seems to manifest this "cylinder condition" and, along with it, simpler mathematics.

In 1926, Oskar Klein gave Kaluza's classical five-dimensional theory a quantum interpretation,^[4][5] to accord with the then-recent discoveries of Werner Heisenberg and Erwin Schrödinger. Klein introduced the hypothesis that the fifth dimension was curled up and microscopic, to explain the cylinder condition. Klein suggested that the geometry of the extra fifth dimension could take the form of a circle, with the radius of 10⁻³⁰ cm. More precisely, the radius of the circular dimension is 23 times the Planck length, which in turn is of the order of 10⁻³³ cm.^[5] Klein also made a contribution to the classical theory by providing a properly normalized 5D metric.^[4] Work continued on the Kaluza field theory during the 1930s by Einstein and colleagues at Princeton University.

In the 1940s, the classical theory was completed, and the full field equations including the scalar field were obtained by three independent research groups:^[6] Yves Thiry,^[7][8][9] working in France on his dissertation under André Lichnerowicz; Pascual Jordan, Günther Ludwig, and Claus Müller in Germany,^{[10][11][12][13][14]} with critical input from Wolfgang Pauli and Markus Fierz; and Paul Scherrer^[15][16][17] working alone in Switzerland. Jordan's work led to the scalar–tensor theory of Brans–Dicke;^[18] Carl H. Brans and Robert H. Dicke were apparently unaware of Thiry or Scherrer. The full Kaluza equations under the cylinder condition are quite complex, and most English-language reviews, as well as the English translations of Thiry, contain some errors. The curvature tensors for the complete Kaluza equations were evaluated using tensor-algebra software in 2015,^[19] verifying results of J. A. Ferrari^[20] and R. Coquereaux & G. Esposito-Farese.^[21] The 5D covariant form of the energy–momentum source terms is treated by L. L. Williams.^[22]

In his 1921 article,^[3] Kaluza established all the elements of the classical five-dimensional theory: the Kaluza–Klein metric, the Kaluza–Klein–Einstein field equations, the equations of motion, the stress–energy tensor, and the cylinder condition. With no free parameters, it merely extends general relativity to five dimensions. One starts by hypothesizing a form of the five-dimensional Kaluza–Klein metric ${\displaystyle {\widetilde {g}}_{ab}}$, where Latin indices span five dimensions. Let one also introduce the four-dimensional spacetime metric ${\displaystyle {g}_{\mu \nu }}$, where Greek indices span the usual four dimensions of space and time; a 4-vector ${\displaystyle A^{\mu }}$ identified with the electromagnetic vector potential; and a scalar field ${\displaystyle \phi }$. Then decompose the 5D metric so that the 4D metric is framed by the electromagnetic vector potential, with the scalar field at the fifth diagonal. This can be visualized as

${\displaystyle {\widetilde {g}}_{ab}\equiv {\begin{bmatrix}g_{\mu \nu }+\phi ^{2}A_{\mu }A_{\nu }&\phi ^{2}A_{\mu }\\\phi ^{2}A_{\nu }&\phi ^{2}\end{bmatrix}}.}$

One can write more precisely

${\displaystyle {\widetilde {g}}_{\mu \nu }\equiv g_{\mu \nu }+\phi ^{2}A_{\mu }A_{\nu },\qquad {\widetilde {g}}_{5\nu }\equiv {\widetilde {g}}_{\nu 5}\equiv \phi ^{2}A_{\nu },\qquad {\widetilde {g}}_{55}\equiv \phi ^{2},}$

where the index ${\displaystyle 5}$ indicates the fifth coordinate by convention, even though the first four coordinates are indexed with 0, 1, 2, and 3. The associated inverse metric is

${\displaystyle {\widetilde {g}}^{ab}\equiv {\begin{bmatrix}g^{\mu \nu }&-A^{\mu }\\-A^{\nu }&g_{\alpha \beta }A^{\alpha }A^{\beta }+{\frac {1}{\phi ^{2}}}\end{bmatrix}}.}$

This decomposition is quite general, and all terms are dimensionless. Kaluza then applies the machinery of standard

, and one finds that electric charge is identified with motion in the fifth dimension.

The hypothesis for the metric implies an invariant five-dimensional length element ${\displaystyle ds}$:

${\displaystyle ds^{2}\equiv {\widetilde {g}}_{ab}\,dx^{a}\,dx^{b}=g_{\mu \nu }\,dx^{\mu }\,dx^{\nu }+\phi ^{2}(A_{\nu }\,dx^{\nu }+dx^{5})^{2}.}$

The Kaluza–Klein–Einstein field equations of the five-dimensional theory were never adequately provided by Kaluza or Klein because they ignored the scalar field. The full Kaluza field equations are generally attributed to Thiry,^[8] who obtained vacuum field equations, although Kaluza^[3] originally provided a stress–energy tensor for his theory, and Thiry included a stress–energy tensor in his thesis. But as described by Gonner,^[6] several independent groups worked on the field equations in the 1940s and earlier. Thiry is perhaps best known only because an English translation was provided by Applequist, Chodos, & Freund in their review book.^[23] Applequist et al. also provided an English translation of Kaluza's article. Translations of the three (1946, 1947, 1948) Jordan articles can be found on the ResearchGate and Academia.edu archives.^[10][11][13] The first correct English-language Kaluza field equations, including the scalar field, were provided by Williams.^[19]

To obtain the 5D Kaluza–Klein–Einstein field equations, the 5D Kaluza–Klein–Christoffel symbols ${\displaystyle {\widetilde {\Gamma }}_{bc}^{a}}$ are calculated from the 5D Kaluza–Klein metric ${\displaystyle {\widetilde {g}}_{ab}}$, and the 5D

${\displaystyle {\widetilde {R}}_{ab}}$ is calculated from the 5D connections.

The classic results of Thiry and other authors presume the cylinder condition:

${\displaystyle {\frac {\partial {\widetilde {g}}_{ab}}{\partial x^{5}}}=0.}$

Without this assumption, the field equations become much more complex, providing many more degrees of freedom that can be identified with various new fields. Paul Wesson and colleagues have pursued relaxation of the cylinder condition to gain extra terms that can be identified with the matter fields,^[24] for which Kaluza^[3] otherwise inserted a stress–energy tensor by hand.

It has been an objection to the original Kaluza hypothesis to invoke the fifth dimension only to negate its dynamics. But Thiry argued^[6] that the interpretation of the Lorentz force law in terms of a five-dimensional geodesic militates strongly for a fifth dimension irrespective of the cylinder condition. Most authors have therefore employed the cylinder condition in deriving the field equations. Furthermore, vacuum equations are typically assumed for which

${\displaystyle {\widetilde {R}}_{ab}=0,}$

where

${\displaystyle {\widetilde {R}}_{ab}\equiv \partial _{c}{\widetilde {\Gamma }}_{ab}^{c}-\partial _{b}{\widetilde {\Gamma }}_{ca}^{c}+{\widetilde {\Gamma }}_{cd}^{c}{\widetilde {\Gamma }}_{ab}^{d}-{\widetilde {\Gamma }}_{bd}^{c}{\widetilde {\Gamma }}_{ac}^{d}}$

and

${\displaystyle {\widetilde {\Gamma }}_{bc}^{a}\equiv {\frac {1}{2}}{\widetilde {g}}^{ad}(\partial _{b}{\widetilde {g}}_{dc}+\partial _{c}{\widetilde {g}}_{db}-\partial _{d}{\widetilde {g}}_{bc}).}$

The vacuum field equations obtained in this way by Thiry^[8] and Jordan's group^[10][11][13] are as follows.

The field equation for ${\displaystyle \phi }$ is obtained from

${\displaystyle {\widetilde {R}}_{55}=0\Rightarrow \Box \phi ={\frac {1}{4}}\phi ^{3}F^{\alpha \beta }F_{\alpha \beta },}$

where ${\displaystyle F_{\alpha \beta }\equiv \partial _{\alpha }A_{\beta }-\partial _{\beta }A_{\alpha },}$ ${\displaystyle \Box \equiv g^{\mu \nu }\nabla _{\mu }\nabla _{\nu },}$ and ${\displaystyle \nabla _{\mu }}$ is a standard, 4D covariant derivative. It shows that the electromagnetic field is a source for the scalar field. Note that the scalar field cannot be set to a constant without constraining the electromagnetic field. The earlier treatments by Kaluza and Klein did not have an adequate description of the scalar field and did not realize the implied constraint on the electromagnetic field by assuming the scalar field to be constant.

The field equation for ${\displaystyle A^{\nu }}$ is obtained from

${\displaystyle {\widetilde {R}}_{5\alpha }=0={\frac {1}{2\phi }}g^{\beta \mu }\nabla _{\mu }(\phi ^{3}F_{\alpha \beta })-A_{\alpha }\phi \Box \phi .}$

It has the form of the vacuum Maxwell equations if the scalar field is constant.

The field equation for the 4D Ricci tensor ${\displaystyle R_{\mu \nu }}$ is obtained from

${\displaystyle {\begin{aligned}{\widetilde {R}}_{\mu \nu }-{\frac {1}{2}}{\widetilde {g}}_{\mu \nu }{\widetilde {R}}&=0\Rightarrow \\R_{\mu \nu }-{\frac {1}{2}}g_{\mu \nu }R&={\frac {1}{2}}\phi ^{2}\left(g^{\alpha \beta }F_{\mu \alpha }F_{\nu \beta }-{\frac {1}{4}}g_{\mu \nu }F_{\alpha \beta }F^{\alpha \beta }\right)+{\frac {1}{\phi }}(\nabla _{\mu }\nabla _{\nu }\phi -g_{\mu \nu }\Box \phi ),\end{aligned}}}$

where ${\displaystyle R}$ is the standard 4D Ricci scalar.

This equation shows the remarkable result, called the "Kaluza miracle", that the precise form for the electromagnetic stress–energy tensor emerges from the 5D vacuum equations as a source in the 4D equations: field from the vacuum. This relation allows the definitive identification of ${\displaystyle A^{\mu }}$ with the electromagnetic vector potential. Therefore, the field needs to be rescaled with a conversion constant ${\displaystyle k}$ such that ${\displaystyle A^{\mu }\to kA^{\mu }}$.

The relation above shows that we must have

${\displaystyle {\frac {k^{2}}{2}}={\frac {8\pi G}{c^{4}}}{\frac {1}{\mu _{0}}}={\frac {2G}{c^{2}}}4\pi \epsilon _{0},}$

where ${\displaystyle G}$ is the gravitational constant, and ${\displaystyle \mu _{0}}$ is the

. In the Kaluza theory, the gravitational constant can be understood as an electromagnetic coupling constant in the metric. There is also a stress–energy tensor for the scalar field. The scalar field behaves like a variable gravitational constant, in terms of modulating the coupling of electromagnetic stress–energy to spacetime curvature. The sign of ${\displaystyle \phi ^{2}}$ in the metric is fixed by correspondence with 4D theory so that electromagnetic energy densities are positive. It is often assumed that the fifth coordinate is spacelike in its signature in the metric.

In the presence of matter, the 5D vacuum condition cannot be assumed. Indeed, Kaluza did not assume it. The full field equations require evaluation of the 5D

${\displaystyle {\widetilde {G}}_{ab}\equiv {\widetilde {R}}_{ab}-{\frac {1}{2}}{\widetilde {g}}_{ab}{\widetilde {R}},}$

as seen in the recovery of the electromagnetic stress–energy tensor above. The 5D curvature tensors are complex, and most English-language reviews contain errors in either ${\displaystyle {\widetilde {G}}_{ab}}$ or ${\displaystyle {\widetilde {R}}_{ab}}$, as does the English translation of Thiry.^[8] In 2015, a complete set of 5D curvature tensors under the cylinder condition, evaluated using tensor-algebra software, was produced.^[19]

The equations of motion are obtained from the five-dimensional geodesic hypothesis^[3] in terms of a 5-velocity ${\displaystyle {\widetilde {U}}^{a}\equiv dx^{a}/ds}$:

${\displaystyle {\widetilde {U}}^{b}{\widetilde {\nabla }}_{b}{\widetilde {U}}^{a}={\frac {d{\widetilde {U}}^{a}}{ds}}+{\widetilde {\Gamma }}_{bc}^{a}{\widetilde {U}}^{b}{\widetilde {U}}^{c}=0.}$

This equation can be recast in several ways, and it has been studied in various forms by authors including Kaluza,^[3] Pauli,^[25] Gross & Perry,^[26] Gegenberg & Kunstatter,^[27] and Wesson & Ponce de Leon,^[28] but it is instructive to convert it back to the usual 4-dimensional length element ${\displaystyle c^{2}\,d\tau ^{2}\equiv g_{\mu \nu }\,dx^{\mu }\,dx^{\nu }}$, which is related to the 5-dimensional length element ${\displaystyle ds}$ as given above:

${\displaystyle ds^{2}=c^{2}\,d\tau ^{2}+\phi ^{2}(kA_{\nu }\,dx^{\nu }+dx^{5})^{2}.}$

Then the 5D geodesic equation can be written^[29] for the spacetime components of the 4-velocity:

${\displaystyle U^{\nu }\equiv {\frac {dx^{\nu }}{d\tau }},}$

${\displaystyle {\frac {dU^{\nu }}{d\tau }}+{\widetilde {\Gamma }}_{\alpha \beta }^{\mu }U^{\alpha }U^{\beta }+2{\widetilde {\Gamma }}_{5\alpha }^{\mu }U^{\alpha }U^{5}+{\widetilde {\Gamma }}_{55}^{\mu }(U^{5})^{2}+U^{\mu }{\frac {d}{d\tau }}\ln {\frac {c\,d\tau }{ds}}=0.}$

The term quadratic in ${\displaystyle U^{\nu }}$ provides the 4D geodesic equation plus some electromagnetic terms:

${\displaystyle {\widetilde {\Gamma }}_{\alpha \beta }^{\mu }=\Gamma _{\alpha \beta }^{\mu }+{\frac {1}{2}}g^{\mu \nu }k^{2}\phi ^{2}(A_{\alpha }F_{\beta \nu }+A_{\beta }F_{\alpha \nu }-A_{\alpha }A_{\beta }\partial _{\nu }\ln \phi ^{2}).}$

The term linear in ${\displaystyle U^{\nu }}$ provides the

:

${\displaystyle {\widetilde {\Gamma }}_{5\alpha }^{\mu }={\frac {1}{2}}g^{\mu \nu }k\phi ^{2}(F_{\alpha \nu }-A_{\alpha }\partial _{\nu }\ln \phi ^{2}).}$

This is another expression of the "Kaluza miracle". The same hypothesis for the 5D metric that provides electromagnetic stress–energy in the Einstein equations, also provides the Lorentz force law in the equation of motions along with the 4D geodesic equation. Yet correspondence with the Lorentz force law requires that we identify the component of 5-velocity along the fifth dimension with electric charge:

${\displaystyle kU^{5}=k{\frac {dx^{5}}{d\tau }}\to {\frac {q}{mc}},}$

where ${\displaystyle m}$ is particle mass, and ${\displaystyle q}$ is particle electric charge. Thus electric charge is understood as motion along the fifth dimension. The fact that the Lorentz force law could be understood as a geodesic in five dimensions was to Kaluza a primary motivation for considering the five-dimensional hypothesis, even in the presence of the aesthetically unpleasing cylinder condition.

Yet there is a problem: the term quadratic in ${\displaystyle U^{5}}$,

${\displaystyle {\widetilde {\Gamma }}_{55}^{\mu }=-{\frac {1}{2}}g^{\mu \alpha }\partial _{\alpha }\phi ^{2}.}$

If there is no gradient in the scalar field, the term quadratic in ${\displaystyle U^{5}}$ vanishes. But otherwise the expression above implies

${\displaystyle U^{5}\sim c{\frac {q/m}{G^{1/2}}}.}$

For elementary particles, ${\displaystyle U^{5}>10^{20}c}$. The term quadratic in ${\displaystyle U^{5}}$ should dominate the equation, perhaps in contradiction to experience. This was the main shortfall of the five-dimensional theory as Kaluza saw it,^[3] and he gives it some discussion in his original article.^{[clarification needed]}

The equation of motion for ${\displaystyle U^{5}}$ is particularly simple under the cylinder condition. Start with the alternate form of the geodesic equation, written for the covariant 5-velocity:

${\displaystyle {\frac {d{\widetilde {U}}_{a}}{ds}}={\frac {1}{2}}{\widetilde {U}}^{b}{\widetilde {U}}^{c}{\frac {\partial {\widetilde {g}}_{bc}}{\partial x^{a}}}.}$

This means that under the cylinder condition, ${\displaystyle {\widetilde {U}}_{5}}$ is a constant of the five-dimensional motion:

${\displaystyle {\widetilde {U}}_{5}={\widetilde {g}}_{5a}{\widetilde {U}}^{a}=\phi ^{2}{\frac {c\,d\tau }{ds}}(kA_{\nu }U^{\nu }+U^{5})={\text{constant}}.}$

Kaluza proposed^[3] a five-dimensional matter stress tensor ${\displaystyle {\widetilde {T}}_{M}^{ab}}$ of the form

${\displaystyle {\widetilde {T}}_{M}^{ab}=\rho {\frac {dx^{a}}{ds}}{\frac {dx^{b}}{ds}},}$

where ${\displaystyle \rho }$ is a density, and the length element ${\displaystyle ds}$ is as defined above.

Then the spacetime component gives a typical "dust" stress–energy tensor:

${\displaystyle {\widetilde {T}}_{M}^{\mu \nu }=\rho {\frac {dx^{\mu }}{ds}}{\frac {dx^{\nu }}{ds}}.}$

The mixed component provides a 4-current source for the Maxwell equations:

${\displaystyle {\widetilde {T}}_{M}^{5\mu }=\rho {\frac {dx^{\mu }}{ds}}{\frac {dx^{5}}{ds}}=\rho U^{\mu }{\frac {q}{kmc}}.}$

Just as the five-dimensional metric comprises the four-dimensional metric framed by the electromagnetic vector potential, the five-dimensional stress–energy tensor comprises the four-dimensional stress–energy tensor framed by the vector 4-current.

Kaluza's original hypothesis was purely classical and extended discoveries of general relativity. By the time of Klein's contribution, the discoveries of Heisenberg, Schrödinger, and Louis de Broglie were receiving a lot of attention. Klein's Nature article^[5] suggested that the fifth dimension is closed and periodic, and that the identification of electric charge with motion in the fifth dimension can be interpreted as standing waves of wavelength ${\displaystyle \lambda ^{5}}$, much like the electrons around a nucleus in the Bohr model of the atom. The quantization of electric charge could then be nicely understood in terms of integer multiples of fifth-dimensional momentum. Combining the previous Kaluza result for ${\displaystyle U^{5}}$ in terms of electric charge, and a

for momentum ${\displaystyle p^{5}=h/\lambda ^{5}}$, Klein obtained^[5] an expression for the 0th mode of such waves:

${\displaystyle mU^{5}={\frac {cq}{G^{1/2}}}={\frac {h}{\lambda ^{5}}}\quad \Rightarrow \quad \lambda ^{5}\sim {\frac {hG^{1/2}}{cq}},}$

where ${\displaystyle h}$ is the Planck constant. Klein found that ${\displaystyle \lambda ^{5}\sim 10^{-30}}$ cm, and thereby an explanation for the cylinder condition in this small value.

Klein's Zeitschrift für Physik article of the same year,^[4] gave a more detailed treatment that explicitly invoked the techniques of Schrödinger and de Broglie. It recapitulated much of the classical theory of Kaluza described above, and then departed into Klein's quantum interpretation. Klein solved a Schrödinger-like wave equation using an expansion in terms of fifth-dimensional waves resonating in the closed, compact fifth dimension.

This section is empty. You can help by adding to it. (February 2015)

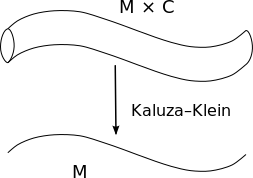
In 1926, Oskar Klein proposed that the fourth spatial dimension is curled up in a circle of a very small

.

In modern geometry, the extra fifth dimension can be understood to be the

noncommutative space

.

The construction can be outlined, roughly, as follows.

principle of least action

, to a single quantity: the scalar curvature on the bundle (as a whole), one obtains simultaneously all of the needed field equations, for both the spacetime and the gauge field.

As an approach to the unification of the forces, it is straightforward to apply the Kaluza–Klein theory in an attempt to unify gravity with the

.

Even in the absence of a completely satisfying theoretical physics framework, the idea of exploring extra, compactified, dimensions is of considerable interest in the

and thus to a discretized thermal energy spectrum.

However, Klein's approach to a quantum theory is flawed^[

Examples of experimental pursuits include work by the

warped models.^{[citation needed}

]

Robert Brandenberger and Cumrun Vafa have speculated that in the early universe, cosmic inflation causes three of the space dimensions to expand to cosmological size while the remaining dimensions of space remained microscopic.^{[citation needed]}

Space–time–matter theory

One particular variant of Kaluza–Klein theory is space–time–matter theory or induced matter theory, chiefly promulgated by Paul Wesson and other members of the Space–Time–Matter Consortium.^[32] In this version of the theory, it is noted that solutions to the equation

${\displaystyle {\widetilde {R}}_{ab}=0}$

may be re-expressed so that in four dimensions, these solutions satisfy

Einstein's equations

${\displaystyle G_{\mu \nu }=8\pi T_{\mu \nu }\,}$

with the precise form of the T_μν following from the

energy–momentum tensor

is normally understood to be due to concentrations of matter in four-dimensional space, the above result is interpreted as saying that four-dimensional matter is induced from geometry in five-dimensional space.

In particular, the soliton solutions of ${\displaystyle {\widetilde {R}}_{ab}=0}$ can be shown to contain the

cosmological models

.

Geometric interpretation

The Kaluza–Klein theory has a particularly elegant presentation in terms of geometry. In a certain sense, it looks just like ordinary gravity in

free space

, except that it is phrased in five dimensions instead of four.

Einstein equations

The equations governing ordinary gravity in free space can be obtained from an

metric on this manifold, one defines the action

S(g) as

${\displaystyle S(g)=\int _{M}R(g)\operatorname {vol} (g),}$

where R(g) is the scalar curvature, and vol(g) is the volume element. By applying the variational principle to the action

${\displaystyle {\frac {\delta S(g)}{\delta g}}=0,}$

one obtains precisely the

Einstein equations

for free space:

${\displaystyle R_{ij}-{\frac {1}{2}}g_{ij}R=0,}$

where R_ij is the

Ricci tensor

.

Maxwell equations

By contrast, the

Maxwell equations describing electromagnetism can be understood to be the Hodge equations of a principal U(1)-bundle or circle bundle

${\displaystyle \pi :P\to M}$ with fiber

U(1). That is, the electromagnetic field

${\displaystyle F}$ is a

harmonic 2-form

in the space ${\displaystyle \Omega ^{2}(M)}$ of differentiable

2-forms

on the manifold ${\displaystyle M}$. In the absence of charges and currents, the free-field Maxwell equations are

${\displaystyle \mathrm {d} F=0\quad {\text{and}}\quad \mathrm {d} {\star }F=0,}$

where ${\displaystyle \star }$ is the Hodge star operator.

Kaluza–Klein geometry

To build the Kaluza–Klein theory, one picks an invariant metric on the circle ${\displaystyle S^{1}}$ that is the fiber of the U(1)-bundle of electromagnetism. In this discussion, an invariant metric is simply one that is invariant under rotations of the circle. Suppose that this metric gives the circle a total length ${\displaystyle \Lambda }$. One then considers metrics ${\displaystyle {\widehat {g}}}$ on the bundle ${\displaystyle P}$ that are consistent with both the fiber metric, and the metric on the underlying manifold ${\displaystyle M}$. The consistency conditions are:

• The projection of ${\displaystyle {\widehat {g}}}$ to the
  vertical subspace
  ${\displaystyle \operatorname {Vert} _{p}P\subset T_{p}P}$ needs to agree with metric on the fiber over a point in the manifold ${\displaystyle M}$.
• The projection of ${\displaystyle {\widehat {g}}}$ to the
  horizontal subspace
  ${\displaystyle \operatorname {Hor} _{p}P\subset T_{p}P}$ of the tangent space at point ${\displaystyle p\in P}$ must be isomorphic to the metric ${\displaystyle g}$ on ${\displaystyle M}$ at ${\displaystyle \pi (P)}$.

The Kaluza–Klein action for such a metric is given by

${\displaystyle S({\widehat {g}})=\int _{P}R({\widehat {g}})\operatorname {vol} ({\widehat {g}}).}$

The scalar curvature, written in components, then expands to

${\displaystyle R({\widehat {g}})=\pi ^{*}\left(R(g)-{\frac {\Lambda ^{2}}{2}}|F|^{2}\right),}$

where ${\displaystyle \pi ^{*}}$ is the pullback of the fiber bundle projection ${\displaystyle \pi :P\to M}$. The connection ${\displaystyle A}$ on the fiber bundle is related to the electromagnetic field strength as

${\displaystyle \pi ^{*}F=dA.}$

That there always exists such a connection, even for fiber bundles of arbitrarily complex topology, is a result from homology and specifically, K-theory. Applying Fubini's theorem and integrating on the fiber, one gets

${\displaystyle S({\widehat {g}})=\Lambda \int _{M}\left(R(g)-{\frac {1}{\Lambda ^{2}}}|F|^{2}\right)\operatorname {vol} (g).}$

Varying the action with respect to the component ${\displaystyle A}$, one regains the Maxwell equations. Applying the variational principle to the base metric ${\displaystyle g}$, one gets the Einstein equations

${\displaystyle R_{ij}-{\frac {1}{2}}g_{ij}R={\frac {1}{\Lambda ^{2}}}T_{ij}}$

with the stress–energy tensor being given by

${\displaystyle T^{ij}=F^{ik}F^{jl}g_{kl}-{\frac {1}{4}}g^{ij}|F|^{2},}$

sometimes called the Maxwell stress tensor.

The original theory identifies ${\displaystyle \Lambda }$ with the fiber metric ${\displaystyle g_{55}}$ and allows ${\displaystyle \Lambda }$ to vary from fiber to fiber. In this case, the coupling between gravity and the electromagnetic field is not constant, but has its own dynamical field, the

radion

.

Generalizations

In the above, the size of the loop ${\displaystyle \Lambda }$ acts as a coupling constant between the gravitational field and the electromagnetic field. If the base manifold is four-dimensional, the Kaluza–Klein manifold P is five-dimensional. The fifth dimension is a

fermions except in very specific cases: the dimension of the total space must be 2 mod 8, and the G-index of the Dirac operator of the compact space must be nonzero.^[33]

The above development generalizes in a more-or-less straightforward fashion to general

supersymmetric

, the resulting theory is a super-symmetric Yang–Mills theory.

Empirical tests

No experimental or observational signs of extra dimensions have been officially reported. Many theoretical search techniques for detecting Kaluza–Klein resonances have been proposed using the mass couplings of such resonances with the top quark. An analysis of results from the LHC in December 2010 severely constrains theories with large extra dimensions.^[34]

The observation of a Higgs-like boson at the LHC establishes a new empirical test which can be applied to the search for Kaluza–Klein resonances and supersymmetric particles. The loop Feynman diagrams that exist in the Higgs interactions allow any particle with electric charge and mass to run in such a loop. Standard Model particles besides the top quark and W boson do not make big contributions to the cross-section observed in the H → γγ decay, but if there are new particles beyond the Standard Model, they could potentially change the ratio of the predicted Standard Model H → γγ cross-section to the experimentally observed cross-section. Hence a measurement of any dramatic change to the H → γγ cross-section predicted by the Standard Model is crucial in probing the physics beyond it.

An article from July 2018

brane theory

. However, the article does demonstrate that electromagnetism and gravity share the same number of dimensions, and this fact lends support to Kaluza–Klein theory; whether the number of dimensions is really 3 + 1 or in fact 4 + 1 is the subject of further debate.

See also

• Classical theories of gravitation
• Complex spacetime
• DGP model
• Quantum gravity
• Compactification (physics)
• Randall–Sundrum model
• Matej Pavšič
• String theory
• Supergravity
• Superstring theory
• Non-relativistic gravitational fields
• Teleparallelism

Notes

1. ^ Nordström, Gunnar (1914). "Über die Möglichkeit, das elektromagnetische Feld und das Gravitationsfeld zu vereinigen" [On the possibility of unifying the gravitational and electromagnetic fields]. Physikalische Zeitschrift (in German). 15: 504.
2. ^ Pais, Abraham (1982). Subtle is the Lord ...: The Science and the Life of Albert Einstein. Oxford: Oxford University Press. pp. 329–330.
3. ^
   Bibcode:1921SPAW.......966K
   .
4. ^
   doi:10.1007/BF01397481
   .
5. ^
   S2CID 4127863
   .
6. ^
   S2CID 13399708
   .
7. ^ Lichnerowicz, A.; Thiry, M. Y. (1947). "Problèmes de calcul des variations liés à la dynamique classique et à la théorie unitaire du champ". Compt. Rend. Acad. Sci. Paris (in French). 224: 529–531.
8. ^ ^{a b c d} Thiry, M. Y. (1948). "Les équations de la théorie unitaire de Kaluza". Compt. Rend. Acad. Sci. Paris (in French). 226: 216–218.
9. ^ Thiry, M. Y. (1948). "Sur la régularité des champs gravitationnel et électromagnétique dans les théories unitaires". Compt. Rend. Acad. Sci. Paris (in French). 226: 1881–1882.
10. ^
    S2CID 20091903
    .
11. ^
    S2CID 93849549
    .
12. S2CID 94454994
    .
13. ^
    doi:10.1002/asna.19482760502
    .
14. S2CID 120176841
    .
15. ^ Scherrer, W. (1941). "Bemerkungen zu meiner Arbeit: "Ein Ansatz für die Wechselwirkung von Elementarteilchen"". Helv. Phys. Acta (in German). 14 (2): 130.
16. ^ Scherrer, W. (1949). "Über den Einfluss des metrischen Feldes auf ein skalares Materiefeld". Helv. Phys. Acta. 22: 537–551.
17. ^ Scherrer, W. (1950). "Über den Einfluss des metrischen Feldes auf ein skalares Materiefeld (2. Mitteilung)". Helv. Phys. Acta (in German). 23: 547–555.
18. doi:10.1103/PhysRev.124.925
    .
19. ^
    doi:10.1155/2015/901870
    .
20. S2CID 121977988
    .
21. ^ Coquereaux, R.; Esposito-Farese, G. (1990). "The theory of Kaluza–Klein–Jordan–Thiry revisited". Annales de l'Institut Henri Poincaré. 52: 113.
22. doi:10.1155/2020/1263723
    .
23. ISBN 978-0-201-09829-7
    .
24. ISBN 978-981-02-3588-8
    .
25. ^ Pauli, Wolfgang (1958). Theory of Relativity (translated by George Field ed.). New York: Pergamon Press. pp. Supplement 23.
26. doi:10.1016/0550-3213(83)90462-5
    .
27. doi:10.1016/0375-9601(84)90980-0
    .
28. Bibcode:1995A&A...294....1W
    .
29. S2CID 122586403
    .
30. ^ David Bleecker, "Gauge Theory and Variational Principles Archived 2021-07-09 at the Wayback Machine" (1982) D. Reidel Publishing (See chapter 9)
31. ^ Ravndal, F., Oskar Klein and the fifth dimension, arXiv:1309.4113 [physics.hist-ph]
32. ^ 5Dstm.org
33. ^ L. Castellani et al., Supergravity and superstrings, vol. 2, ch. V.11.
34. S2CID 122803232
    .
35. S2CID 119197181
    .

References

• Kaluza, Theodor (1921). "Zum Unitätsproblem in der Physik". Sitzungsber. Preuss. Akad. Wiss. Berlin. (Math. Phys.): 966–972.
  Bibcode:1921SPAW.......966K. https://archive.org/details/sitzungsberichte1921preussi
• Klein, Oskar (1926). "Quantentheorie und fünfdimensionale Relativitätstheorie".
  doi:10.1007/BF01397481
  .
• Witten, Edward (1981). "Search for a realistic Kaluza–Klein theory".
  doi:10.1016/0550-3213(81)90021-3
  .
• Appelquist, Thomas; Chodos, Alan; Freund, Peter G. O. (1987). Modern Kaluza–Klein Theories. Menlo Park, Cal.: Addison–Wesley.
  ISBN 978-0-201-09829-7
  . (Includes reprints of the above articles as well as those of other important papers relating to Kaluza–Klein theory.)
• Duff, M. J. (1994). "Kaluza–Klein Theory in Perspective". In Lindström, Ulf (ed.). Proceedings of the Symposium 'The Oskar Klein Centenary'. Singapore: World Scientific. pp. 22–35.
  ISBN 978-981-02-2332-8
  .
• Overduin, J. M.; Wesson, P. S. (1997). "Kaluza–Klein Gravity". Physics Reports. 283 (5): 303–378.
  S2CID 119087814
  .
• Wesson, Paul S. (2006). Five-Dimensional Physics: Classical and Quantum Consequences of Kaluza–Klein Cosmology. Singapore: World Scientific.
  ISBN 978-981-256-661-4
  .

Further reading

• The CDF Collaboration, Search for Extra Dimensions using Missing Energy at CDF, (2004) (A simplified presentation of the search made for extra dimensions at the Collider Detector at Fermilab (CDF) particle physics facility.)
• John M. Pierre, SUPERSTRINGS! Extra Dimensions, (2003).
• Chris Pope, Lectures on Kaluza–Klein Theory.
• Edward Witten (2014). "A Note On Einstein, Bergmann, and the Fifth Dimension",
  arXiv:1401.8048