Planck constant

Planck constant
Common symbols	${\displaystyle h}$
m2 s−1
Dimension	${\displaystyle {\mathsf {M}}{\mathsf {L}}^{2}{\mathsf {T}}^{-1}}$
Value	6.62607015×10−34 J⋅Hz−1 4.135667696...×10−15 eV⋅Hz−1

Reduced Planck constant
Common symbols	${\displaystyle \hbar }$
m2 s −1
Derivations from other quantities	${\displaystyle \hbar {=}h/(2\pi )}$
Dimension	${\displaystyle {\mathsf {M}}{\mathsf {L}}^{2}{\mathsf {T}}^{-1}}$
Value	1.054571817...×10−34 J⋅s 6.582119569...×10−16 eV⋅s

The Planck constant, or Planck's constant, denoted by ${\textstyle h}$,^[1] is a fundamental physical constant^[1] of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a matter wave equals the Planck constant divided by the associated particle momentum.

The constant was postulated by

The SI units are defined in such a way that, when the Planck constant is expressed in SI units, it has the exact value ${\displaystyle h}$ = 6.62607015×10⁻³⁴ J⋅Hz⁻¹.

History

Origin of the constant

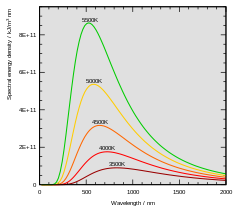
Planck's constant was formulated as part of Max Planck's successful effort to produce a mathematical expression that accurately predicted the observed spectral distribution of thermal radiation from a closed furnace (black-body radiation).^[7] This mathematical expression is now known as Planck's law.

In the last years of the 19th century, Max Planck was investigating the problem of black-body radiation first posed by

Approaching this problem, Planck hypothesized that the equations of motion for light describe a set of harmonic oscillators, one for each possible frequency. He examined how the entropy of the oscillators varied with the temperature of the body, trying to match Wien's law, and was able to derive an approximate mathematical function for the black-body spectrum,^[2] which gave a simple empirical formula for long wavelengths.

Planck tried to find a mathematical expression that could reproduce Wien's law (for short wavelengths) and the empirical formula (for long wavelengths). This expression included a constant, ${\displaystyle h}$, which is thought to be for Hilfsgrösse (auxiliary variable),

${\displaystyle B_{\nu }(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\mathrm {B} }T}}-1}}}$,

where ${\displaystyle k_{\text{B}}}$ is the Boltzmann constant, ${\displaystyle h}$ is the Planck constant, and ${\displaystyle c}$ is the speed of light in the medium, whether material or vacuum.^[9][10][11]

The spectral radiance of a body, ${\displaystyle B_{\nu }}$, describes the amount of energy it emits at different radiation frequencies. It is the power emitted per unit area of the body, per unit solid angle of emission, per unit frequency. The spectral radiance can also be expressed per unit wavelength ${\displaystyle \lambda }$ instead of per unit frequency. In this case, it is given by

${\displaystyle B_{\lambda }(\lambda ,T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\mathrm {B} }T}}-1}}}$,

showing how radiated energy emitted at shorter wavelengths increases more rapidly with temperature than energy emitted at longer wavelengths.^[12]

Planck's law may also be expressed in other terms, such as the number of photons emitted at a certain wavelength, or the energy density in a volume of radiation. The SI units of ${\displaystyle B_{\nu }}$ are W·sr⁻¹·m⁻²·Hz⁻¹, while those of ${\displaystyle B_{\lambda }}$ are W·sr⁻¹·m⁻³.

Planck soon realized that his solution was not unique. There were several different solutions, each of which gave a different value for the entropy of the oscillators.^[2] To save his theory, Planck resorted to using the then-controversial theory of statistical mechanics,^[2] which he described as "an act of desperation".^[13] One of his new boundary conditions was

to interpret U_N [the vibrational energy of N oscillators] not as a continuous, infinitely divisible quantity, but as a discrete quantity composed of an integral number of finite equal parts. Let us call each such part the energy element ε;

— Planck, On the Law of Distribution of Energy in the Normal Spectrum^[2]

With this new condition, Planck had imposed the quantization of the energy of the oscillators, "a purely formal assumption ... actually I did not think much about it ..." in his own words,

${\displaystyle E=hf.}$

Planck was able to calculate the value of ${\displaystyle h}$ from experimental data on black-body radiation: his result, 6.55×10⁻³⁴ J⋅s, is within 1.2% of the currently defined value.^[2] He also made the first determination of the Boltzmann constant ${\displaystyle k_{\text{B}}}$ from the same data and theory.^[15]

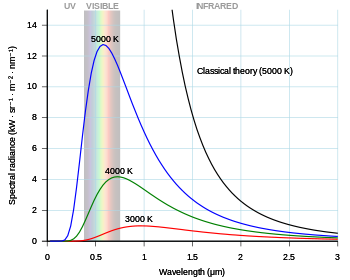
Development and application

The black-body problem was revisited in 1905, when Lord Rayleigh and James Jeans (on the one hand) and Albert Einstein (on the other hand) independently proved that classical electromagnetism could never account for the observed spectrum. These proofs are commonly known as the "ultraviolet catastrophe", a name coined by Paul Ehrenfest in 1911. They contributed greatly (along with Einstein's work on the photoelectric effect) in convincing physicists that Planck's postulate of quantized energy levels was more than a mere mathematical formalism. The first Solvay Conference in 1911 was devoted to "the theory of radiation and quanta".^[16]

Photoelectric effect

The photoelectric effect is the emission of electrons (called "photoelectrons") from a surface when light is shone on it. It was first observed by

Before Einstein's paper, electromagnetic radiation such as visible light was considered to behave as a wave: hence the use of the terms "frequency" and "wavelength" to characterize different types of radiation. The energy transferred by a wave in a given time is called its intensity. The light from a theatre spotlight is more intense than the light from a domestic lightbulb; that is to say that the spotlight gives out more energy per unit time and per unit space (and hence consumes more electricity) than the ordinary bulb, even though the color of the light might be very similar. Other waves, such as sound or the waves crashing against a seafront, also have their intensity. However, the energy account of the photoelectric effect did not seem to agree with the wave description of light.

The "photoelectrons" emitted as a result of the photoelectric effect have a certain kinetic energy, which can be measured. This kinetic energy (for each photoelectron) is independent of the intensity of the light,^[18] but depends linearly on the frequency;^[20] and if the frequency is too low (corresponding to a photon energy that is less than the work function of the material), no photoelectrons are emitted at all, unless a plurality of photons, whose energetic sum is greater than the energy of the photoelectrons, acts virtually simultaneously (multiphoton effect).^[23] Assuming the frequency is high enough to cause the photoelectric effect, a rise in intensity of the light source causes more photoelectrons to be emitted with the same kinetic energy, rather than the same number of photoelectrons to be emitted with higher kinetic energy.^[18]

Einstein's explanation for these observations was that light itself is quantized; that the energy of light is not transferred continuously as in a classical wave, but only in small "packets" or quanta. The size of these "packets" of energy, which would later be named photons, was to be the same as Planck's "energy element", giving the modern version of the Planck–Einstein relation:

${\displaystyle E=hf.}$

Einstein's postulate was later proven experimentally: the constant of proportionality between the frequency of incident light ${\displaystyle f}$ and the kinetic energy of photoelectrons ${\displaystyle E}$ was shown to be equal to the Planck constant ${\displaystyle h}$.^[20]

Atomic structure

In 1912 John William Nicholson developed^[24] an atomic model and found the angular momentum of the electrons in the model were related by h/2π.^[25][26] Nicholson's nuclear quantum atomic model influenced the development of Niels Bohr 's atomic model^[27][28][26] and Bohr quoted him in his 1913 paper of the Bohr model of the atom.^[29] Bohr's model went beyond Planck's abstract harmonic oscillator concept: an electron in a Bohr atom could only have certain defined energies ${\displaystyle E_{n}}$

${\displaystyle E_{n}=-{\frac {hcR_{\infty }}{n^{2}}},}$

where ${\displaystyle c}$ is the speed of light in vacuum, ${\displaystyle R_{\infty }}$ is an experimentally determined constant (the Rydberg constant) and ${\displaystyle n\in \{1,2,3,...\}}$. This approach also allowed Bohr to account for the Rydberg formula, an empirical description of the atomic spectrum of hydrogen, and to account for the value of the Rydberg constant ${\displaystyle R_{\infty }}$ in terms of other fundamental constants. In discussing angular momentum of the electrons in his model Bohr introduced the quantity ${\displaystyle {\frac {h}{2\pi }}}$, now known as the reduced Planck constant as the quantum of angular momentum.^[29]

Uncertainty principle

The Planck constant also occurs in statements of Werner Heisenberg's uncertainty principle. Given numerous particles prepared in the same state, the uncertainty in their position, ${\displaystyle \Delta x}$, and the uncertainty in their momentum, ${\displaystyle \Delta p_{x}}$, obey

${\displaystyle \Delta x\,\Delta p_{x}\geq {\frac {\hbar }{2}},}$

where the uncertainty is given as the

In addition to some assumptions underlying the interpretation of certain values in the quantum mechanical formulation, one of the fundamental cornerstones to the entire theory lies in the commutator relationship between the position operator ${\displaystyle {\hat {x}}}$ and the momentum operator ${\displaystyle {\hat {p}}}$:

${\displaystyle [{\hat {p}}_{i},{\hat {x}}_{j}]=-i\hbar \delta _{ij},}$

where ${\displaystyle \delta _{ij}}$ is the Kronecker delta.

Photon energy

The Planck relation connects the particular photon energy E with its associated wave frequency f:

${\displaystyle E=hf.}$

This energy is extremely small in terms of ordinarily perceived everyday objects.

Since the frequency f, wavelength λ, and speed of light c are related by ${\displaystyle f={\frac {c}{\lambda }}}$, the relation can also be expressed as

${\displaystyle E={\frac {hc}{\lambda }}.}$

de Broglie wavelength

In 1923,

${\displaystyle \lambda ={\frac {h}{p}},}$

where p denotes the linear momentum of a particle, such as a photon, or any other elementary particle.

The energy of a photon with angular frequency ω = 2πf is given by

${\displaystyle E=\hbar \omega ,}$

while its linear momentum relates to

${\displaystyle p=\hbar k,}$

where k is an angular wavenumber.

These two relations are the temporal and spatial parts of the special relativistic expression using

${\displaystyle P^{\mu }=\left({\frac {E}{c}},{\vec {p}}\right)=\hbar K^{\mu }=\hbar \left({\frac {\omega }{c}},{\vec {k}}\right).}$

Statistical mechanics

Classical

${\displaystyle h}$ = 6.62607015×10⁻³⁴ J⋅Hz⁻¹[5]

${\displaystyle \hbar ={h \over 2\pi }}$ = 1.054571817...×10⁻³⁴ J⋅s^[33] = 6.582119569...×10⁻¹⁶ eV⋅s.^[34]

The above values have been adopted as fixed in the 2019 redefinition of the SI base units.

Since 2019, the numerical value of the Planck constant has been fixed, with a

The Planck constant is one of the smallest constants used in physics. This reflects the fact that on a scale adapted to humans, where energies are typical of the order of kilojoules and times are typical of the order of seconds or minutes, the Planck constant is very small. When the product of energy and time for a physical event approaches the Planck constant, quantum effects dominate.^[36]

Equivalently, the order of the Planck constant reflects the fact that everyday objects and systems are made of a large number of microscopic particles. For example, in green light (with a wavelength of 555 nanometres or a frequency of 540 THz) each photon has an energy E = hf = 3.58×10⁻¹⁹ J. That is a very small amount of energy in terms of everyday experience, but everyday experience is not concerned with individual photons any more than with individual atoms or molecules. An amount of light more typical in everyday experience (though much larger than the smallest amount perceivable by the human eye) is the energy of one mole of photons; its energy can be computed by multiplying the photon energy by the Avogadro constant, N_A = 6.02214076×10²³ mol^−1[37], with the result of 216 kJ, about the food energy in three apples.^{[citation needed]}

Reduced Planck constant ℏ

In many applications, the Planck constant ${\textstyle h}$ naturally appears in combination with ${\textstyle 2\pi }$ as ${\textstyle h/(2\pi )}$, which can be traced to the fact that in these applications it is natural to use the angular frequency (in radians per second) rather than plain frequency (in cycles per second or hertz). For this reason, it is often useful to absorb that factor of 2π into the Planck constant by introducing the reduced Planck constant^{[38][39]: 482} (or reduced Planck's constant^{[40]: 5  [41]: 788}), equal to the Planck constant divided by ${\textstyle 2\pi }$^[38] and denoted by ${\textstyle \hbar }$ (pronounced h-bar^[42]: 336).

Many of the most important equations, relations, definitions, and results of quantum mechanics are customarily written using the reduced Planck constant ${\textstyle \hbar }$ rather than the Planck constant ${\textstyle h}$, including the

The fundamental equations look simpler when written using ${\textstyle \hbar }$ as opposed to ${\textstyle h}$, and it is usually ${\textstyle \hbar }$ rather than ${\textstyle h}$ that gives the most reliable results when used in order-of-magnitude estimates. For example, using dimensional analysis to estimate the ionization energy of a hydrogen atom, the relevant parameters that determine the ionization energy ${\textstyle E_{\text{i}}}$ are the mass of the electron ${\textstyle m_{\text{e}}}$, the electron charge ${\textstyle e}$, and either the Planck constant ${\textstyle h}$ or the reduced Planck constant ${\textstyle \hbar }$:

$${\displaystyle E_{\text{i}}\propto m_{\text{e}}e^{4}/h^{2}\ {\text{or}}\ \propto m_{\text{e}}e^{4}/\hbar ^{2}}$$

${\textstyle \hbar }$

${\textstyle h}$

${\textstyle (2\pi )^{2}\approx 40}$.

Names

The reduced Planck constant is known by many other names: the rationalized Planck constant^{[45]: 726  [46]: 10  [47]: -} (or rationalized Planck's constant^{[48]: 334  [49]: ix} ,^[50]: 112 the Dirac constant^{[51]: 275  [45]: 726  [52]: xv} (or Dirac's constant^{[53]: 148  [54]: 604  [55]: 313}), the Dirac ${\textstyle h}$^{[56][57]: xviii} (or Dirac's ${\textstyle h}$^[58]: 17 ), the Dirac ${\textstyle \hbar }$^[59]: 187 (or Dirac's ${\textstyle \hbar }$^{[60]: 273  [61]: 14} ), and h-bar.^{[62]: 558 [63]: 561} It is also common to refer to this ${\textstyle \hbar }$ as "Planck's constant"^{[64]: 55  [a]} while retaining the relationship ${\textstyle \hbar =h/(2\pi )}$.

Symbols

By far the most common symbol for the reduced Planck constant is ${\textstyle \hbar }$ . However, there are some sources that denote it by ${\textstyle h}$ instead, in which case they usually refer to it as the "Dirac ${\textstyle h}$"^{[90]: 43  [91]: 151} (or "Dirac's ${\textstyle h}$"^[92]: 21).

History

The combination ${\textstyle h/(2\pi )}$ appeared in Niels Bohr's 1913 paper,^[93]: 15 where it was denoted by ${\textstyle M_{0}}$.^{[26]: 169 [b]} For the next 15 years, the combination continued to appear in the literature, but normally without a separate symbol.^{[94]: 180 [c]} Then, in 1926, in their seminal papers, Schrödinger and Dirac again introduced special symbols for it: ${\textstyle K}$ in the case of Schrödinger,^[106] and ${\textstyle h}$ in the case of Dirac.^[107] Dirac continued to use ${\textstyle h}$ in this way until 1930,^[108]: 291 when he introduced the symbol ${\textstyle \hbar }$ in his book The Principles of Quantum Mechanics.^{[108]: 291  [109]}

See also

• Committee on Data of the International Science Council
• International System of Units
• Introduction to quantum mechanics
• List of scientists whose names are used in physical constants
• Planck units
• Wave–particle duality

Notes

References

Citations