NAND logic

.

The mathematical proof for this was published by Henry M. Sheffer in 1913 in the Transactions of the American Mathematical Society (Sheffer 1913). A similar case applies to the NOR function, and this is referred to as NOR logic.

NAND

A NAND gate is an inverted AND gate. It has the following truth table:

Q = A NAND B Truth Table Input A Input B Output Q 0 0 1 0 1 1 1 0 1 1 1 0

In

transistors (top half) will conduct, and a conductive path will be established between the output and Vss (ground), bringing the output low. If both of the A and B inputs are low, then neither of the NMOS transistors will conduct, while both of the PMOS transistors will conduct, establishing a conductive path between the output and Vdd (voltage source), bringing the output high. If either of the A or B inputs is low, one of the NMOS transistors will not conduct, one of the PMOS transistors will, and a conductive path will be established between the output and Vdd (voltage source), bringing the output high. As the only configuration of the two inputs that results in a low output is when both are high, this circuit implements a NAND (NOT AND) logic gate.

Making other gates by using NAND gates

A NAND gate is a

, meaning that any other gate can be represented as a combination of NAND gates.

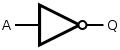
NOT

A NOT gate is made by joining the inputs of a NAND gate together. Since a NAND gate is equivalent to an AND gate followed by a NOT gate, joining the inputs of a NAND gate leaves only the NOT gate.

Desired NOT Gate	NAND Construction
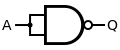
Q = NOT( A )	= A NAND A
Truth Table Input A Output Q 0 1 1 0

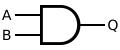
AND

An AND gate is made by inverting the output of a NAND gate as shown below.

Desired AND Gate	NAND Construction
Q = A AND B	= ( A NAND B ) NAND ( A NAND B )
Truth Table Input A Input B Output Q 0 0 0 0 1 0 1 0 0 1 1 1

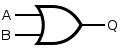
OR

If the truth table for a NAND gate is examined or by applying

, it can be seen that if any of the inputs are 0, then the output will be 1. To be an OR gate, however, the output must be 1 if any input is 1. Therefore, if the inputs are inverted, any high input will trigger a high output.

Desired OR Gate	NAND Construction
Q = A OR B	= ( A NAND A ) NAND ( B NAND B )
Truth Table Input A Input B Output Q 0 0 0 0 1 1 1 0 1 1 1 1

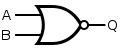
NOR

A NOR gate is an OR gate with an inverted output. Output is high when neither input A nor input B is high.

Desired NOR Gate	NAND Construction
Q = A NOR B	= [ ( A NAND A ) NAND ( B NAND B ) ] NAND [ ( A NAND A ) NAND ( B NAND B ) ]
Truth Table Input A Input B Output Q 0 0 1 0 1 0 1 0 0 1 1 0

XOR

An XOR gate is made by connecting four NAND gates as shown below. This construction entails a propagation delay three times that of a single NAND gate.

Desired XOR Gate	NAND Construction
Q = A XOR B	= [ A NAND ( A NAND B ) ] NAND [ B NAND ( A NAND B ) ]
Truth Table Input A Input B Output Q 0 0 0 0 1 1 1 0 1 1 1 0

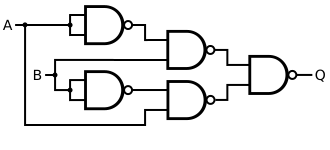
Alternatively, an XOR gate is made by considering the disjunctive normal form ${\displaystyle A\cdot {\overline {B}}+{\overline {A}}\cdot B}$, noting from

that a NAND gate is an inverted-input OR gate. This construction uses five gates instead of four.

Desired Gate	NAND Construction
Q = A XOR B	= [ B NAND ( A NAND A ) ] NAND [ A NAND ( B NAND B ) ]

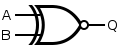
XNOR

An XNOR gate is made by considering the disjunctive normal form ${\displaystyle A\cdot B+{\overline {A}}\cdot {\overline {B}}}$, noting from

that a NAND gate is an inverted-input OR gate. This construction entails a propagation delay three times that of a single NAND gate and uses five gates.

Desired XNOR Gate	NAND Construction
Q = A XNOR B	= [ ( A NAND A ) NAND ( B NAND B ) ] NAND ( A NAND B )
Input A Input B Output Q 0 0 1 0 1 0 1 0 0 1 1 1

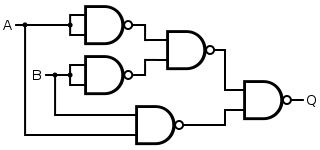
Alternatively, the 4-gate version of the XOR gate can be used with an inverter. This construction has a propagation delay four times (instead of three times) that of a single NAND gate.

Desired Gate	NAND Construction
Q = A XNOR B	= { [ A NAND ( A NAND B ) ] NAND [ B NAND ( A NAND B ) ] } NAND { [ A NAND ( A NAND B ) ] NAND [ B NAND ( A NAND B ) ] }

MUX

A multiplexer or a MUX gate is a three-input gate that uses one of the inputs, called the selector bit, to select one of the other two inputs, called data bits, and outputs only the selected data bit.^[1]

Desired MUX Gate	NAND Construction
Q = [ A AND NOT( S ) ] OR ( B AND S )	= [ A NAND ( S NAND S ) ] NAND ( B NAND S )
Truth Table Input A Input B Select Output Q 0 0 0 0 0 1 0 0 1 0 0 1 1 1 0 1 0 0 1 0 0 1 1 1 1 0 1 0 1 1 1 1

DEMUX

A demultiplexer performs the opposite function of a multiplexer: It takes a single input and channels it to one of two possible outputs according to a selector bit that specifies which output to choose.^{[1][copyright violation?]}

Desired DEMUX Gate	NAND Construction
Truth Table Input Select Output A Output B 0 0 0 0 1 0 1 0 0 1 0 0 1 1 0 1

See also

• CMOS transistor structures and chip deposition geometries that produce NAND logic elements
• Sheffer stroke – other name
• NOR logic. Like NAND gates, NOR gates are also universal gates.
• Functional completeness

References

External links

• TTL NAND and AND gates - All About Circuits
• Steps to Derive XOR from NAND gate.
• NandGame - a game about building a computer using only NAND gates