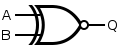
XNOR gate

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "XNOR gate" – news · newspapers · books · scholar · JSTOR (September 2020) (Learn how and when to remove this message)

XNOR gate truth table
Input		Output
A	B	A XNOR B
0	0	1
0	1	0
1	0	0
1	1	1

Logical connectives
AND ${\displaystyle A\land B}$, ${\displaystyle A\cdot B}$, ${\displaystyle AB}$, ${\displaystyle A\&B}$, ${\displaystyle A\&\&B}$ equivalent ${\displaystyle A\equiv B}$, ${\displaystyle A\Leftrightarrow B}$, ${\displaystyle A\leftrightharpoons B}$ implies ${\displaystyle A\Rightarrow B}$, ${\displaystyle A\supset B}$, ${\displaystyle A\rightarrow B}$ NAND ${\displaystyle A{\overline {\land }}B}$, ${\displaystyle A\uparrow B}$, ${\displaystyle A\mid B}$, ${\displaystyle {\overline {A\cdot B}}}$ nonequivalent ${\displaystyle A\not \equiv B}$, ${\displaystyle A\not \Leftrightarrow B}$, ${\displaystyle A\nleftrightarrow B}$ NOR ${\displaystyle A{\overline {\lor }}B}$, ${\displaystyle A\downarrow B}$, ${\displaystyle {\overline {A+B}}}$ NOT ${\displaystyle \neg A}$, ${\displaystyle -A}$, ${\displaystyle {\overline {A}}}$, ${\displaystyle \sim A}$ OR ${\displaystyle A\lor B}$, ${\displaystyle A+B}$, ${\displaystyle A\mid B}$, ${\displaystyle A\parallel B}$ XNOR ${\displaystyle A\ {\text{XNOR}}\ B}$ XOR ${\displaystyle A{\underline {\lor }}B}$, ${\displaystyle A\oplus B}$ converse ${\displaystyle A\Leftarrow B}$, ${\displaystyle A\subset B}$, ${\displaystyle A\leftarrow B}$
Related concepts
Propositional calculus Predicate logic Boolean algebra Truth table Truth function Boolean function Functional completeness
Applications
Digital logic Programming languages Mathematical logic Philosophy of logic
Category
v t e

The XNOR gate (sometimes ENOR, EXNOR, NXOR, XAND and pronounced as Exclusive NOR) is a digital

It is equivalent to the logical connective (${\displaystyle \leftrightarrow }$) from mathematical logic, also known as the material biconditional. The two-input version implements logical equality, behaving according to the truth table to the right, and hence the gate is sometimes called an "equivalence gate". A high output (1) results if both of the inputs to the gate are the same. If one but not both inputs are high (1), a low output (0) results.

The algebraic notation used to represent the XNOR operation is ${\displaystyle S=A\odot B}$. The algebraic expressions ${\displaystyle (A+{\overline {B}})\cdot ({\overline {A}}+B)}$ and ${\displaystyle A\cdot B+{\overline {A}}\cdot {\overline {B}}}$ both represent the XNOR gate with inputs A and B.

Symbols

There are two symbols for XNOR gates: one with distinctive shape and one with rectangular shape and label. Both symbols for the XNOR gate are that of the XOR gate with an added inversion bubble.

Hardware description

XNOR gates are represented in most

implementation). Both include four independent, two-input, XNOR gates. The (now obsolete) 74S135 implemented four two-input XOR/XNOR gates or two three-input XNOR gates.

Both the TTL

formats (SOIC-14, SOC-14 or TSSOP-14).

Datasheets are readily available in most datasheet databases and suppliers.

Implementation

AND-OR-Invert logic

An XNOR gate can be implemented using a NAND gate and an OR-AND-Invert gate, as shown in the following picture. ^[3] This is based on the identity

${\displaystyle {\overline {a\veebar b}}\iff \left(a{\overline {\land }}b\right){\overline {\land }}\left(a\lor b\right)}$

An alternative, which is useful when inverted inputs are also available (for example from a

gate, shown on below on the right.

• 
  XNOR implemention using a NAND and an OAI gate
• 
  XNOR implementation using a 2-2-AOI gate with normal and inverted inputs

CMOS

CMOS implementations based on the OAI logic above can be realized with 10

, as shown below. The implementation which uses both normal and inverted inputs uses 8 transistors, or 12 if inverters have to be used.

• 
  An XNOR-gate in CMOS using a NAND and an OR-AND-Invert gate
• 
  An XNOR gate in CMOS using both normal and inverted inputs

Pinout

Both the 4077 and 74x266 devices (SN74LS266, 74HC266, 74266, etc.) have the same pinout diagram, as follows:

Pinout diagram of the 74HC266N, 74LS266 and CD4077 quad XNOR plastic

.

Alternatives

If a specific type of gate is not available, a circuit that implements the same function can be constructed from other available gates. A circuit implementing an XNOR function can be trivially constructed from an XOR gate followed by a NOT gate. If we consider the expression ${\displaystyle (A+{\overline {B}})\cdot ({\overline {A}}+B)}$, we can construct an XNOR gate circuit directly using AND, OR and NOT gates. However, this approach requires five gates of three different kinds.

As alternative, if different gates are available we can apply Boolean algebra to transform ${\displaystyle (A+{\overline {B}})\cdot ({\overline {A}}+B)\equiv (A\cdot B)+({\overline {A}}\cdot {\overline {B}})}$ as stated above, and apply

to the last term to get ${\displaystyle (A\cdot B)+{\overline {(A+B)}}}$ which can be implemented using only three gates as shown on the right.

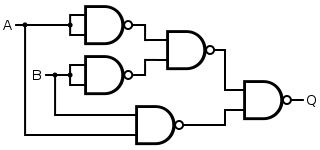
An XNOR gate circuit can be made from four NOR gates. In fact, both NAND and NOR gates are so-called "universal gates" and any logical function can be constructed from either NAND logic or NOR logic alone. If the four NOR gates are replaced by NAND gates, this results in an XOR gate, which can be converted to an XNOR gate by inverting the output or one of the inputs (e.g. with a fifth NAND gate).

Desired gate	NAND construction	NOR construction

An alternative arrangement is of five NAND gates in a topology that emphasizes the construction of the function from ${\displaystyle (A\cdot B)+({\overline {A}}\cdot {\overline {B}})}$, noting from

that a NAND gate is an inverted-input OR gate. Another alternative arrangement is of five NOR gates in a topology that emphasizes the construction of the function from ${\displaystyle (A+{\overline {B}})\cdot ({\overline {A}}+B)}$, noting from that a NOR gate is an inverted-input AND gate.

Desired gate	NAND construction	NOR construction

For the NAND constructions, the lower arrangement offers the advantage of a shorter propagation delay (the time delay between an input changing and the output changing). For the NOR constructions, the upper arrangement requires fewer gates.

From the opposite perspective, constructing other gates using only XNOR gates is possible though XNOR is not a fully universal logic gate. NOT and XOR gates can be constructed this way.

More than two inputs

Although other gates (OR, NOR, AND, NAND) are available from manufacturers with three or more inputs per gate, this is not strictly true with XOR and XNOR gates. However, extending the concept of the

logical operation to three inputs, the SN74S135 with two shared "C" and four independent "A" and "B" inputs for its four outputs, was a device that followed the truth table:

Input			Output
A	B	C	Q
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

This is effectively Q = NOT ((A XOR B) XOR C). Another way to interpret this is that the output is true if an even number of inputs are true. It does not implement a logical "equivalence" function, unlike two-input XNOR gates.

See also

• AND gate
• OR gate
• NOT gate
• NAND gate
• NOR gate
• XOR gate
• Kronecker delta function
• Logical biconditional
• If and only if

References

External links

• Texas Instruments© CD4077 Datasheet