Quine–Putnam indispensability argument

Edit links
Source: Wikipedia, the free encyclopedia.

Willard Quine
Photo of Hilary Putnam
Hilary Putnam

The Quine–Putnam indispensability argument

Willard Quine and Hilary Putnam
, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as

no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy:[2]

  • We ought to have ontological commitment to all and only the entities that are indispensable to our best scientific theories.
  • Mathematical entities are indispensable to our best scientific theories.
  • Therefore, we ought to have ontological commitment to mathematical entities.

Nominalists, philosophers who reject the existence of abstract objects, have argued against both premises of this argument. An influential argument by Hartry Field claims that mathematical entities are dispensable to science. This argument has been supported by attempts to demonstrate that scientific and mathematical theories can be reformulated to remove all references to mathematical entities. Other philosophers, including Penelope Maddy, Elliott Sober, and Joseph Melia, have argued that we do not need to believe in all of the entities that are indispensable to science. The arguments of these writers inspired a new explanatory version of the argument, which Alan Baker and Mark Colyvan support, that argues mathematics is indispensable to specific scientific explanations as well as whole theories.

Background

In his 1973 paper "Mathematical Truth",

causal theory of knowledge, that we would not be able to know about such objects because they cannot come into causal contact with us.[c][8] This is called Benacerraf's epistemological problem because it concerns the epistemology of mathematics, that is, how we come to know what we do about mathematics.[9]

The philosophy of mathematics is split into two main strands:

platonism and nominalism. Platonism holds that there exist abstract mathematical objects such as numbers and sets whilst nominalism denies their existence.[10] Each of these views faces issues due to the problem raised by Benacerraf. Because nominalism rejects the existence of mathematical objects, it faces no epistemological problem but it does face problems concerning the idea that mathematics should not have its own special semantics. Platonism does not face problems concerning the semantic half of the dilemma but it has difficulty explaining how we can have any knowledge about mathematical objects.[11]

The indispensability argument aims to overcome the epistemological problem posed against platonism by providing a justification for belief in abstract mathematical objects.[5] It is part of a broad class of indispensability arguments most commonly applied in the philosophy of mathematics, but which also includes arguments in the philosophy of language and ethics.[12] In the most general sense, indispensability arguments aim to support their conclusion based on the claim that the truth of the conclusion is indispensable or necessary for a certain purpose.[13] When applied in the field of ontology—the study of what exists—they exemplify a Quinean strategy for establishing the existence of controversial entities that cannot be directly investigated. According to this strategy, the indispensability of these entities for formulating a theory of other less controversial entities counts as evidence for their existence.[14] In the case of philosophy of mathematics, the indispensability of mathematical entities for formulating scientific theories is taken as evidence for the existence of those mathematical entities.[15]

Overview of the argument

Mark Colyvan presents the argument in the Stanford Encyclopedia of Philosophy in the following form:[2]

  • We ought to have ontological commitment to all and only the entities that are indispensable to our best scientific theories.
  • Mathematical entities are indispensable to our best scientific theories.
  • Therefore, we ought to have ontological commitment to mathematical entities.

Here, an ontological commitment to an entity is a commitment to believing that that entity exists.

scientific realists as it attempts to justify belief in mathematical entities in a manner similar to the justification for belief in theoretical entities such as electrons or quarks; Quine held that such nominalists have a "double standard" with regards to ontology.[2]

The indispensability argument differs from other arguments for platonism because it only argues for belief in the parts of mathematics that are indispensable to science. It does not necessarily justify belief in the most abstract parts of set theory, which Quine (

necessary truths.[20]

Whilst Quine's original argument is an argument for platonism, indispensability arguments can also be constructed to argue for the weaker claim of sentence realism—the claim that mathematical theory is objectively true. This is a weaker claim because it does not necessarily imply there are abstract mathematical objects.[21]

Major concepts

Indispensability

The second premise of the indispensability argument states mathematical objects are indispensable to our best scientific theories. In this context, indispensability is not the same as ineliminability because any entity can be eliminated from a theoretical system given appropriate adjustments to the other parts of the system.

empirical adequacy and simplicity.[23] Furthermore, if an entity is dispensable to a theory, an equivalent theory can be formulated without it.[24] This is the case, for example, if each sentence in one theory is a paraphrase of a sentence in another or if the two theories predict the same empirical observations.[25]

According to the Stanford Encyclopedia of Philosophy, one of the most influential arguments against the indispensability argument comes from

Newtonian physics in terms of the relationships between space-time points. Instead of referring to numerical distances, Field's reformulation uses relationships such as "between" and "congruent" to recover the theory without implying the existence of numbers.[29] John Burgess and Mark Balaguer have taken steps to extend this nominalizing project to areas of modern physics, including quantum mechanics.[30] Philosophers such as David Malament and Otávio Bueno dispute whether such reformulations are successful or even possible, particularly in the case of quantum mechanics.[31]

Field's alternative to platonism is

mathematical fictionalism, according to which mathematical theories are false because they refer to abstract objects which do not exist.[32] As part of his argument against the indispensability argument, Field has tried to explain how it is possible for false mathematical statements to be used by science without making scientific predictions false.[33] His argument is based on the idea that mathematics is conservative. A mathematical theory is conservative if, when combined with a scientific theory, it does not imply anything about the physical world that the scientific theory alone would not have already.[34] This explains how it is possible for mathematics to be used by scientific theories without making the predictions of science false. In addition, Field has attempted to specify how exactly mathematics is useful in application.[26] Field thinks mathematics is useful for science because mathematical language provides a useful shorthand for talking about complex physical systems.[30]

Another approach to denying that mathematical entities are indispensable to science is to reformulate mathematical theories themselves so they do not imply the existence of mathematical objects. Charles Chihara, Geoffrey Hellman, and Putnam have offered modal reformulations of mathematics that replace all references to mathematical objects with claims about possibilities.[30]

Naturalism

The naturalism underlying the indispensability argument is a form of

Eleatic principle. According to this principle there are only causal entities and no non-causal entities.[38] Quine's naturalism claims such a principle cannot be used to overturn our best scientific theories' ontological commitment to mathematical entities because philosophical principles cannot overrule science.[39]

I'm moved to laughter at the thought of how presumptuous it would be to reject mathematics for philosophical reasons. How would you like the job of telling the mathematicians that they must change their ways, and abjure countless errors, now that philosophy has discovered that there are no classes? Can you tell them, with a straight face, to follow philosophical argument wherever it may lead? If they challenge your credentials, will you boast of philosophy's other great discoveries: that motion is impossible, that a Being than which no greater can be conceived cannot be conceived not to exist, ... and so on, and on, ad nauseam? Not me!

David Lewis, Parts of Classes[40]

Quine held his naturalism as a fundamental assumption but later philosophers have provided arguments to support it. The most common arguments in support of Quinean naturalism are track-record arguments. These are arguments that appeal to science's successful track record compared to philosophy and other disciplines.[41] David Lewis (1991) famously made such an argument in a passage from his 1991 book Parts of Classes, deriding the track record of philosophy compared to mathematics and arguing that the idea of philosophy overriding science is absurd.[42] Critics of the track record argument have argued that it goes too far, discrediting philosophical arguments and methods entirely, and contest the idea that philosophy can be uniformly judged to have had a bad track record.[43]

Quine's naturalism has also been criticized by Penelope Maddy for contradicting mathematical practice.[44] According to the indispensability argument, mathematics is subordinated to the natural sciences in the sense that its legitimacy depends on them.[45] But Maddy (1992) argues mathematicians do not seem to believe their practice is restricted in any way by the activity of the natural sciences. For example, mathematicians' arguments over the axioms of Zermelo–Fraenkel set theory do not appeal to their applications to the natural sciences. Similarly, Charles Parsons has argued that mathematical truths seem immediately obvious in a way that suggests they do not depend on the results of our best theories.[46]

Confirmational holism

Confirmational holism is the view that scientific theories and hypotheses cannot be confirmed in isolation and must be confirmed together as part of a larger cluster of theories.[47] An example of this idea provided by Michael Resnik is of the hypothesis that an observer will see oil and water separate out if they are added together because they do not mix. This hypothesis cannot be confirmed in isolation because it relies on assumptions such as the absence of any chemical that will interfere with their separation and that the eyes of the observer are functioning well enough to observe the separation.[48] Because mathematical theories are likewise assumed by scientific theories, confirmational holism implies the empirical confirmations of scientific theories also support these mathematical theories.[49]

According to a counterargument by Maddy (1992), the theses of naturalism and confirmational holism that make up the first premise of the indispensability argument are in tension with one another. Maddy said naturalism tells us that we should respect the methods used by scientists as the best method for uncovering the truth, but scientists do not seem to act as though we should believe in all of the entities that are indispensable to science.[50] To illustrate this point, Maddy uses the example of atomic theory; she said that despite the atom being indispensable to scientists' best theories by 1860, their reality was not universally accepted until 1913 when they were put to a direct experimental test.[51] Maddy and others such as Mary Leng also appeal to the fact that scientists use mathematical idealizations, such as assuming bodies of water to be infinitely deep, without regard for the trueness of such applications of mathematics.[52] According to Maddy, this indicates that scientists do not view the indispensable use of mathematics for science as justification for the belief in mathematics or mathematical entities. Overall, Maddy said we should side with naturalism and reject confirmational holism, meaning we do not need to believe in all of the entities that are indispensable to science.[26]

Another counterargument due to Elliott Sober (1993) claims that mathematical theories are not tested in the same way as scientific theories. Whilst scientific theories compete with alternatives to find which theory has the most empirical support, there are no alternatives for mathematical theory to compete with because all scientific theories share the same mathematical core. As a result, according to Sober, mathematical theories do not share the empirical support of our best scientific theories so we should reject confirmational holism.[53]

Since these counterarguments have been raised, a number of philosophers—including Resnik, Alan Baker, Patrick Dieveney, David Liggins, Jacob Busch, and Andrea Sereni—have argued that confirmational holism can be eliminated from the argument.[54] For example, Resnik (1995, p. 171) has offered a pragmatic indispensability argument that "claims that the justification for doing science ... also justifies our accepting as true such mathematics as science uses".[55]

Ontological commitment

Another key part of the argument is the concept of

existential quantifier for Quine was the natural equivalent of the ordinary language term "there is", which he believed obviously carries ontological commitment.[57] Quine thought it is important to translate our best scientific theories into first-order logic because ordinary language is ambiguous, whereas logic can make the commitments of a theory more precise. Translating theories to first-order logic also has advantages over translating them to higher-order logics such as second-order logic. Whilst second-order logic has the same expressive power as first-order logic, it lacks some of the technical strengths of first-order logic such as completeness and compactness. Second-order logic also allows quantification over properties like "redness", but whether we have ontological commitment to properties is controversial.[16] According to Quine, such quantification is simply ungrammatical.[58]

Jody Azzouni has objected to Quine's criterion of ontological commitment, saying that the existential quantifier in first-order logic need not be interpreted as always carrying ontological commitment.[59] According to Azzouni, the ordinary language equivalent of existential quantification "there is" is often used in sentences without implying ontological commitment. In particular, Azzouni (2004, pp. 68–69) points to the use of "there is" when referring to fictional objects in sentences such as "there are fictional detectives who are admired by some real detectives".[60] According to Azzouni, for us to have ontological commitment to an entity, we must have the right level of epistemic access to it. This means, for example, that it must overcome some epistemic burdens for us to be able to postulate it. But according to Azzouni (2004, p. 127), mathematical entities are "mere posits" that can be postulated by anyone at any time by "simply writing down a set of axioms", so we do not need to treat them as real.[61]

More modern presentations of the argument do not necessarily accept Quine's criterion of ontological commitment and may allow for ontological commitments to be directly determined from ordinary language.[62][d]

Mathematical explanation

In his counterargument, Joseph Melia (1998, pp. 70–71) argues that the role of mathematics in science is not genuinely explanatory and is solely used to "make more things sayable about concrete objects".[64] He appeals to a practice he calls weaseling, which occurs when a person makes a statement and then later withdraws something implied by that statement. An example of weaseling is the statement: "Everyone who came to the seminar had a handout. But the person who came in late didn't get one."[65] Whilst this statement can be interpreted as being self-contradictory, it is more charitable to interpret it as coherently making the claim: "Except for the person who came in late, everyone who came to the seminar had a handout."[65] Melia said a similar situation occurs in scientists' use of statements that imply the existence of mathematical objects. According to Melia (2000, p. 489), whilst scientists use statements that imply the existence of mathematics in their theories, "almost all scientists ... deny that there are such things as mathematical objects".[65] As in the seminar-handout example, Melia said it is most charitable to interpret scientists not as contradicting themselves, but rather as weaseling away their commitment to mathematical objects. According to Melia, because this weaseling is not a genuinely explanatory use of mathematical language, it is acceptable to not believe in the mathematical objects that scientists weasel away.[64]

Inspired by Maddy's and Sober's arguments against confirmational holism,

inference to the best explanation. It states we are justified in believing in mathematical objects because they appear in our best scientific explanations, not because they inherit the empirical support of our best theories.[71] It is presented by the Internet Encyclopedia of Philosophy in the following form:[68]

  • There are genuinely mathematical explanations of empirical phenomena.
  • We ought to be committed to the theoretical posits in such explanations.
  • Therefore, we ought to be committed to the entities postulated by the mathematics in question.
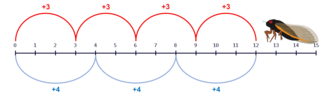
Number line with multiples of 3 and 4 highlighted up to the number 12. An illustration of a cicada sits at the number 13.
Number line visualizing why prime-numbered life cycles are advantageous compared to non-prime life cycles. If predators have life cycles of 3 or 4 years, they quickly synchronize with a non-prime life cycle such as a life cycle of 12 years. But they will not synchronize with a 13-year periodical cicada's life cycle until 39 and 52 years have passed, respectively.

An example of mathematics' explanatory indispensability presented by Baker (

seven bridges of Königsberg only once in a walk across the city.[73] The main response to this form of the argument, which philosophers such as Melia, Chris Daly, Simon Langford, and Juha Saatsi adopted, is to deny there are genuinely mathematical explanations of empirical phenomena, instead framing the role of mathematics as representational or indexical.[74]

Historical development

Precursors and influences on Quine

A photo of Gottlob Frege
Aspects of the indispensability argument can be traced back to Gottlob Frege.

The argument is historically associated with

Willard Quine and Hilary Putnam but it can be traced to earlier thinkers such as Gottlob Frege and Kurt Gödel. In his arguments against mathematical formalism—a view that argues that mathematics is akin to a game like chess with rules about how mathematical symbols such as "2" can be manipulated—Frege (2017, §91) said in 1893 that "it is applicability alone which elevates arithmetic from a game to the rank of a science".[75] Gödel (1947, §3), in a paper on the axioms of set theory, said that if a new axiom were to have enough verifiable consequences, it "would have to be accepted at least in the same sense as any well‐established physical theory".[75] Frege's and Gödel's arguments differ from the later Quinean indispensability argument because they lack features such as naturalism and subordination of practice, leading some philosophers, including Pieranna Garavaso (2005), to say that they are not genuine examples of the indispensability argument.[76]

Whilst developing his philosophical view of confirmational holism, Quine was influenced by

unfalsifiable.[48] These critics based this claim on the fact that the law does not make any observable predictions without positing some observational frame of reference and that falsifying instances can always be avoided by changing the choice of reference frame. Duhem responded by saying that the law produces predictions when paired with auxiliary hypotheses fixing the frame of reference and is therefore no different from any other physical theory.[78] Duhem said that although individual hypotheses may make no observable predictions alone, they can be confirmed as parts of systems of hypotheses. Quine extended this idea to mathematical hypotheses, claiming that although mathematical hypotheses hold no empirical content on their own, they can share in the empirical confirmations of the systems of hypotheses in which they are contained.[79] This thesis later came to be known as the Duhem–Quine thesis.[80]

Quine (

logical positivists, such as his teacher Rudolf Carnap; his naturalism was formulated in response to many of their ideas.[83] For the logical positivists, all justified beliefs were reducible to sense data, including our knowledge of ordinary objects such as trees.[84] Quine criticized sense data as self-defeating, saying that we must believe in ordinary objects to organize our experiences of the world. He also said that because science is our best theory of how sense-experience gives us beliefs about ordinary objects, we should believe in it as well.[85] Whilst the logical positivists said that individual claims must be supported by sense data, Quine's confirmational holism means scientific theory is inherently tied up with mathematical theory and so evidence for scientific theories can justify belief in mathematical objects despite their not being directly perceived.[84]

Quine and Putnam

Whilst he eventually became a platonist due to his formulation of the indispensability argument,[86] Quine was sympathetic to nominalism from the early stages of his career.[87] In a 1946 lecture, he said: "I will put my cards on the table now and avow my prejudices: I should like to be able to accept nominalism" (Quine 2008, p. 6).[88] Nelson Goodman and Quine (1947) subsequently released a joint 1947 paper titled "Steps toward a Constructive Nominalism" as part of an ongoing project of Quine's to "set up a nominalistic language in which all of natural science can be expressed" (Quine 1939, p. 708).[89] In a letter to Joseph Henry Woodger the following year, however, Quine said that he was becoming more convinced "the assumption of abstract entities and the assumptions of the external world are assumptions of the same sort".[90] He later released the 1948 paper "On What There Is", in which he said that "[t]he analogy between the myth of mathematics and the myth of physics is ... strikingly close" (Quine 1948, p. 37), marking a shift towards his eventual acceptance of a "reluctant platonism".[91]

Throughout the 1950s, Quine regularly mentioned platonism, nominalism, and constructivism as plausible views, and he had not yet reached a definitive conclusion about which is correct.[92] It is unclear exactly when Quine accepted platonism; in 1953, he distanced himself from the claims of nominalism in his 1947 paper with Goodman, but by 1956, Goodman (1956) was still describing Quine's "defection" from nominalism as "still somewhat tentative".[93] According to Lieven Decock, Quine had accepted the need for abstract mathematical entities by the publication of his 1960 book Word and Object, in which he wrote "a thoroughgoing nominalist doctrine is too much to live up to" (Quine 1960, p. 269).[94] However, whilst he released suggestions of the indispensability argument in a number of papers, he never gave it a detailed formulation.[95]

Putnam gave the argument its first explicit presentation in his 1971 book Philosophy of Logic in which he attributed it to Quine.[96] He stated the argument as "quantification over mathematical entities is indispensable for science, both formal and physical; therefore we should accept such quantification; but this commits us to accepting the existence of the mathematical entities in question" (Putnam 1971, p. 347).[97] He also wrote Quine had "for years stressed both the indispensability of quantification over mathematical entities and the intellectual dishonesty of denying the existence of what one daily presupposes" (Putnam 1971, p. 347).[97] Putnam's endorsement of Quine's version of the argument is disputed. The Internet Encyclopedia of Philosophy states: "In his early work, Hilary Putnam accepted Quine's version of the indispensability argument."[98] Liggins also states that the argument has been attributed to Putnam by many philosophers of mathematics. Liggins and Bueno, however, said Putnam never endorsed the argument and only presented it as an argument from Quine.[99] Putnam has said he differed with Quine in his attitude to the argument from at least 1975.[100] Features of the argument that Putnam came to disagree with include its reliance on a single, regimented, best theory.[98]

In 1975, Putnam formulated his own indispensability argument based on the

no miracles argument in the philosophy of science, which argues the success of science can only be explained by scientific realism without being rendered miraculous. He wrote that year (Putnam 1979, p. 73): "I believe that the positive argument for realism [in science] has an analogue in the case of mathematical realism. Here too, I believe, realism is the only philosophy that doesn't make the success of the science a miracle."[98] The Internet Encyclopedia of Philosophy terms this version of the argument "Putnam's success argument" and presents it in the following form:[98]

According to the Internet Encyclopedia of Philosophy, the first and second premises of the argument have been seen as uncontroversial, so discussion of this argument has been focused on the third premise. Other positions that have attempted to provide a reason for the success of mathematics include Field's reformulations of science, which explain the usefulness of mathematics as a conservative shorthand.[98] Putnam has criticized Field's reformulations for only applying to classical physics and for being unlikely to be able to be extended to future fundamental physics.[103]

Continued development of the argument

Chihara (1973), in Ontology and the Vicious Circle Principle, was one of the earliest philosophers to attempt to reformulate mathematics in response to Quine's arguments.[104] Field (1980) followed with Science Without Numbers and dominated discussion about the indispensability argument throughout the 1980s and 1990s.[105] With the introduction of arguments against the first premise of the argument, initially by Maddy in the 1990s and continued by Melia and others in the 2000s, Field's approach has come to be known as "Hard Road Nominalism" due to the difficulty of creating technical reconstructions of science that it requires. Approaches attacking the first premise, in contrast, have come to be known as "Easy Road Nominalism".[106]

Colyvan (1998, 2001) is often seen as presenting the standard or "canonical" formulation of the argument within more recent philosophical work.[107] Colyvan's version of the argument has been influential in debates in contemporary philosophy of mathematics.[108] It differs in key ways from the arguments presented by Quine and Putnam. Quine's version of the argument relies on translating scientific theories from ordinary language into first-order logic to determine its ontological commitments whereas the modern version allows ontological commitments to be directly determined from ordinary language. Putnam's arguments were for the objectivity of mathematics but not necessarily for mathematical objects.[109] Putnam has explicitly distanced himself from this version of the argument, saying, "from my point of view, Colyvan's description of my argument(s) is far from right", and has contrasted his indispensability argument with "the fictitious 'Quine–Putnam indispensability argument'".[110] Colyvan has said "the attribution to Quine and Putnam [is] an acknowledgement of intellectual debts rather than an indication that the argument, as presented, would be endorsed in every detail by either Quine or Putnam".[111]

Influence

According to James Franklin, the indispensability argument is widely considered to be the best argument for platonism in the philosophy of mathematics.[112] The Stanford Encyclopedia of Philosophy identifies it as one of the major arguments in the debate between mathematical realism and mathematical anti-realism; according to the Stanford Encyclopedia of Philosophy, some within the field see it as the only good argument for platonism.[113]

Quine's and Putnam's arguments have also been influential outside philosophy of mathematics, inspiring indispensability arguments in other areas of philosophy. For example,

truthmakers, modality, and possible worlds.[115] In the field of ethics, David Enoch (2011) has expanded the criterion of ontological commitment used in the Quine–Putnam indispensability argument to argue for moral realism. According to Enoch's "deliberative indispensability argument", indispensability to deliberation is just as ontologically committing as indispensability to science, and moral facts are indispensable to deliberation. Therefore, according to Enoch, we should believe in moral facts.[116]

Notes

  1. ^ Also referred to as the Putnam–Quine indispensability argument, holism–naturalism indispensability argument[1] or simply the indispensability argument
  2. ^ The concerns Benacerraf raised date back at least to Plato and Socrates, and were given detailed attention in the late nineteenth century prior to Quine and Putnam's arguments, which were raised in the 1960s and 1970s.[3] In contemporary philosophy, however, Benacerraf's presentation of these problems is considered to be the classic one.[4]
  3. ^ Subsequent philosophers have generalized this problem beyond the causal theory of knowledge; for Hartry Field, the general problem is to provide a mechanism explaining how mathematical beliefs can accurately reflect the properties of abstract mathematical objects.[8]
  4. ^ Non-Quinean forms of the argument can also be constructed using alternative criteria of ontological commitment. For example, Sam Baron (2013) defends a version of the argument that depends on a criterion of ontological commitment based on truthmaker theory.[63]
  5. ^ Baker identifies Field (1989) as originating this form of the argument, while other philosophers argue he was the first to raise the connection between indispensability and explanation but did not fully formulate an explanatory version of the indispensability argument.[69] Other thinkers who anticipated certain details of the explanatory form of the argument include Mark Steiner (1978a, 1978b) and J. J. C. Smart (1990).[70]
  6. ^ According to the Internet Encyclopedia of Philosophy, this version of the argument can be used to argue for platonism or sentence realism.[98] However, Putnam himself used it to argue for sentence realism.[101] Putnam's view is a reformulation of mathematics in terms of modal logic that maintains mathematical objectivity without being committed to mathematical objects.[102]

References

Citations

  1. ^ Decock 2002, p. 236.
  2. ^ a b c Colyvan 2019, §1.
  3. ^ Molinini, Pataut & Sereni 2016, p. 318.
  4. ^ Balaguer 2018, §1.5.
  5. ^ a b c Marcus, Introduction.
  6. ^ Colyvan 2012, pp. 9–10.
  7. ^ Paseau & Baker 2023, p. 2; Colyvan 2012, p. 1.
  8. ^ a b Colyvan 2012, pp. 10–12.
  9. ^ Horsten 2019, §3.4; Colyvan 2019, §6.
  10. ^ Colyvan 2012, pp. 8–9.
  11. ^ Shapiro 2000, pp. 31–32; Colyvan 2012, pp. 9–10.
  12. ^ Panza & Sereni 2015, pp. 470–471; Sinclair & Leibowitz 2016, pp. 10–18.
  13. ^ Colyvan 2019, Introduction.
  14. ^ Panza & Sereni 2016, p. 470.
  15. ^ Colyvan 2019.
  16. ^ a b Marcus, §2.
  17. ^ a b c Colyvan 2019, §3.
  18. ^ Maddy 2005, p. 437.
  19. ^ Colyvan 2019, §2; Marcus, §7; Bostock 2009, pp. 276–277.
  20. ^ Marcus, §7; Colyvan 2001, Ch. 6.
  21. ^ Panza & Sereni 2013, p. 201.
  22. ^ Colyvan 2019, §2. See also footnote 3 there.
  23. ^ Colyvan 2019, §2.
  24. ^ Busch & Sereni 2012, p. 347.
  25. ^ Panza & Sereni 2013, pp. 205–207.
  26. ^ a b c Colyvan 2019, §4.
  27. ^ Colyvan 2019, §4; Colyvan 2001, p. 69; Linnebo 2017, pp. 105–106.
  28. ^ Linnebo 2017, pp. 105–106.
  29. ^ Colyvan 2001, p. 72.
  30. ^ a b c Marcus, §7.
  31. ^ Balaguer 2018, §2.1; Bueno 2020, §3.3.2.
  32. ^ Balaguer 2018, Introduction.
  33. ^ Colyvan 2019, §4; Colyvan 2001, pp. 70–71; Linnebo 2017, pp. 105–106.
  34. ^ Colyvan 2001, p. 71; Paseau & Baker 2023, p. 14.
  35. ^ Paseau & Baker 2023, p. 4.
  36. ^ Colyvan 2001, pp. 23–24.
  37. ^ Colyvan 2001, p. 25.
  38. ^ Colyvan 2001, pp. 32–33.
  39. ^ Colyvan 2001, pp. 32–33; Bangu 2012, pp. 16–17.
  40. ^ Weatherson 2021, §7.1.
  41. ^ Paseau & Baker 2023, p. 6.
  42. ^ Paseau & Baker 2023, p. 6; Weatherson 2021, §7.1.
  43. ^ Paseau & Baker 2023, p. 7.
  44. ^ Colyvan 2001, p. 93.
  45. ^ Marcus, §6; Colyvan 2001, p. 93.
  46. ^ Horsten 2019, §3.2; Colyvan 2019, §4; Bostock 2009, p. 278.
  47. ^ Resnik 2005, p. 414; Paseau & Baker 2023, p. 9.
  48. ^ a b Resnik 2005, p. 414.
  49. ^ Horsten 2019, §3.2.
  50. ^ Colyvan 2019, §4; Paseau & Baker 2023, p. 23.
  51. ^ Colyvan 2001, p. 92; Paseau & Baker 2023, pp. 22–23.
  52. ^ Colyvan 2019, §4; Paseau & Baker 2023, pp. 24–25.
  53. ^ Colyvan 2019, §4; Bostock 2009, p. 278; Resnik 2005, p. 419.
  54. ^ Marcus 2014.
  55. ^ Colyvan 2001, p. 14–15.
  56. ^ Leng 2010, pp. 39–40.
  57. ^ Marcus, §2; Bangu 2012, pp. 26–28.
  58. ^ Burgess 2013, p. 287.
  59. ^ Bangu 2012, p. 28; Bueno 2020, §5.
  60. ^ Antunes 2018, p. 16.
  61. ^ Bueno 2020, §5; Colyvan 2012, p. 64; Shapiro 2000, p. 251.
  62. ^ Liggins 2008, §5.
  63. ^ Asay 2020, p. 226.
  64. ^ a b Liggins 2012, pp. 998–999; Knowles & Liggins 2015, pp. 3398–3399; Daly & Langford 2009, pp. 641–644.
  65. ^ a b c Liggins 2012, pp. 998–999; Knowles & Liggins 2015, pp. 3398–3399.
  66. ^ Colyvan 2019, §5.
  67. ^ Mancosu 2018, §3.2; Bangu 2013, pp. 256–258.
  68. ^ a b Marcus, §5.
  69. ^ Molinini, Pataut & Sereni 2016, p. 320; Bangu 2013, pp. 255–256; Marcus 2015, Ch. 7, §3.
  70. ^ Colyvan 2019, Bibliography.
  71. ^ Marcus 2014, pp. 3583–3584; Leng 2005; Paseau & Baker 2023, p. 37.
  72. ^ Colyvan 2019, §5; Paseau & Baker 2023, pp. 35–36.
  73. ^ Molinini, Pataut & Sereni 2016, p. 321; Bangu 2012, pp. 152–153; Ginammi 2016, p. 64.
  74. ^ Molinini 2016, p. 405.
  75. ^ a b Colyvan 2001, pp. 8–9.
  76. ^ Marcus, §6; Sereni 2015.
  77. ^ Maddy 2007, p. 91.
  78. ^ Resnik 2005, p. 415.
  79. ^ Resnik 2005, pp. 414–415.
  80. ^ Paseau & Baker 2023, p. 10.
  81. ^ Marcus, §2a; Shapiro 2000, p. 212.
  82. ^ Maddy 2005, p. 438.
  83. ^ Shapiro 2000, p. 212; Marcus, §2a.
  84. ^ a b Marcus, §2a.
  85. ^ Maddy 2007, p. 442; Marcus, §2a.
  86. ^ Putnam 2012, p. 223; Paseau & Baker 2023, p. 2.
  87. ^ Mancosu 2010; Decock 2002, p. 235.
  88. ^ Mancosu 2010, p. 398.
  89. ^ Mancosu 2010, p. 398; Verhaegh 2018, p. 112; Paseau & Baker 2023, pp. 2–3.
  90. ^ Mancosu 2010, p. 402.
  91. ^ Verhaegh 2018, p. 113; Mancosu 2010, p. 403.
  92. ^ Decock 2002, p. 235.
  93. ^ Burgess 2013, p. 290.
  94. ^ Decock 2002, p. 235..
  95. ^ Marcus, §2; Paseau & Baker 2023, p. 1.
  96. ^ Bueno 2018, pp. 202–203; Shapiro 2000, p. 216; Sereni 2015, footnote 2.
  97. ^ a b Bueno 2018, p. 205; Liggins 2008, §4; Decock 2002, p. 231.
  98. ^ a b c d e f Marcus, §3.
  99. ^ Liggins 2008, pp. 115, 123; Bueno 2018, pp. 202–203.
  100. ^ Putnam 2012, p. 183.
  101. ^ Colyvan 2001, pp. 2–3.
  102. ^ Bueno 2013, p. 227; Bueno 2018, pp. 201–202; Colyvan 2001, pp. 2–3; Putnam 2012, pp. 182–183.
  103. ^ Putnam 2012, pp. 190–192.
  104. ^ Burgess & Rosen 1997, p. 196.
  105. ^ Knowles & Liggins 2015, p. 3398.
  106. ^ Paseau & Baker 2023, pp. 30–31.
  107. ^ Molinini, Pataut & Sereni 2016, p. 320; Bueno 2018, p. 203.
  108. ^ Sereni 2015, §2.1; Marcus 2014, p. 3576.
  109. ^ Colyvan 2019, Introduction; Liggins 2008, §5.
  110. ^ Putnam 2012, pp. 182, 186.
  111. ^ Colyvan 2019, footnote 1.
  112. ^ Franklin 2009, p. 134.
  113. ^ Colyvan 2019, §6.
  114. ^ Weatherson 2021, §6.1; Nolan 2005, pp. 204–205.
  115. ^ Melia 2017, p. 96.
  116. ^ Sinclair & Leibowitz 2016, pp. 15–16; McPherson & Plunkett 2015, pp. 104–105.

Sources

Further reading
Retrieved from "https://en.wikipedia.org/w/index.php?title=Quine–Putnam_indispensability_argument&oldid=1186304452"