Category (mathematics)
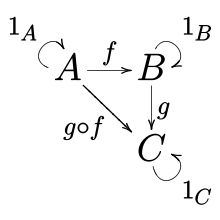
In
Category theory is a branch of mathematics that seeks to generalize all of mathematics in terms of categories, independent of what their objects and arrows represent. Virtually every branch of modern mathematics can be described in terms of categories, and doing so often reveals deep insights and similarities between seemingly different areas of mathematics. As such, category theory provides an alternative foundation for mathematics to set theory and other proposed axiomatic foundations. In general, the objects and arrows may be abstract entities of any kind, and the notion of category provides a fundamental and abstract way to describe mathematical entities and their relationships.
In addition to formalizing mathematics, category theory is also used to formalize many other systems in computer science, such as the
Two categories are the same if they have the same collection of objects, the same collection of arrows, and the same associative method of composing any pair of arrows. Two different categories may also be considered "equivalent" for purposes of category theory, even if they do not have precisely the same structure.
Well-known categories are denoted by a short capitalized word or abbreviation in bold or italics: examples include
The classic and still much used text on category theory is Categories for the Working Mathematician by Saunders Mac Lane. Other references are given in the References below. The basic definitions in this article are contained within the first few chapters of any of these books.
Totalityα
|
Associativity
|
Identity | Divisibilityβ | Commutativity
| |
|---|---|---|---|---|---|
| Partial magma | Unneeded | Unneeded | Unneeded | Unneeded | Unneeded |
| Semigroupoid | Unneeded | Required | Unneeded | Unneeded | Unneeded |
| Small category | Unneeded | Required | Required | Unneeded | Unneeded |
| Groupoid | Unneeded | Required | Required | Required | Unneeded |
| Magma | Required | Unneeded | Unneeded | Unneeded | Unneeded |
| Quasigroup | Required | Unneeded | Unneeded | Required | Unneeded |
Unital magma
|
Required | Unneeded | Required | Unneeded | Unneeded |
Loop
|
Required | Unneeded | Required | Required | Unneeded |
| Semigroup | Required | Required | Unneeded | Unneeded | Unneeded |
| Associative quasigroup | Required | Required | Unneeded | Required | Unneeded |
| Monoid | Required | Required | Required | Unneeded | Unneeded |
Commutative monoid
|
Required | Required | Required | Unneeded | Required |
| Group | Required | Required | Required | Required | Unneeded |
| Abelian group | Required | Required | Required | Required | Required |
| ^α The closure axiom, used by many sources and defined differently, is equivalent. ^β Here, divisibility refers specifically to the quasigroup axioms. | |||||
Any monoid can be understood as a special sort of category (with a single object whose self-morphisms are represented by the elements of the monoid), and so can any preorder.
Definition
There are many equivalent definitions of a category.[1] One commonly used definition is as follows. A category C consists of
- a class ob(C) of objects,
- a class mor(C) of morphisms or arrows,
- a domain or source class function dom: mor(C) → ob(C),
- a codomain or target class function cod: mor(C) → ob(C),
- for every three objects a, b and c, a binary operation hom(a, b) × hom(b, c) → hom(a, c) called composition of morphisms. Here hom(a, b) denotes the subclass of morphisms f in mor(C) such that dom(f) = a and cod(f) = b. Morphisms in this subclass are written f : a → b, and the composite of f : a → b and g : b → c is often written as g ∘ f or gf.
such that the following axioms hold:
- the associative law: if f : a → b, g : b → c and h : c → d then h ∘ (g ∘ f) = (h ∘ g) ∘ f, and
- the (left and right unit laws): for every object x, there exists a morphism 1x : x → x (some authors write idx) called the identity morphism for x, such that every morphism f : a → x satisfies 1x ∘ f = f, and every morphism g : x → b satisfies g ∘ 1x = g.
We write f: a → b, and we say "f is a morphism from a to b". We write hom(a, b) (or homC(a, b) when there may be confusion about to which category hom(a, b) refers) to denote the hom-class of all morphisms from a to b.[2]
Some authors write the composite of morphisms in "diagrammatic order", writing f;g or fg instead of g ∘ f.
From these axioms, one can prove that there is exactly one identity morphism for every object. Often the map assigning each object its identity morphism is treated as an extra part of the structure of a category, namely a class function i: ob(C) → mor(C). Some authors use a slight variant of the definition in which each object is identified with the corresponding identity morphism. This stems from the idea that the fundamental data of categories are morphisms and not objects. In fact, categories can be defined without reference to objects at all using a partial binary operation with additional properties.
Small and large categories
A category C is called small if both ob(C) and hom(C) are actually
Examples
The
Any class can be viewed as a category whose only morphisms are the identity morphisms. Such categories are called discrete. For any given set I, the discrete category on I is the small category that has the elements of I as objects and only the identity morphisms as morphisms. Discrete categories are the simplest kind of category.
Any preordered set (P, ≤) forms a small category, where the objects are the members of P, the morphisms are arrows pointing from x to y when x ≤ y. Furthermore, if ≤ is antisymmetric, there can be at most one morphism between any two objects. The existence of identity morphisms and the composability of the morphisms are guaranteed by the reflexivity and the transitivity of the preorder. By the same argument, any partially ordered set and any equivalence relation can be seen as a small category. Any ordinal number can be seen as a category when viewed as an ordered set.
Any
Similarly any group can be seen as a category with a single object in which every morphism is invertible, that is, for every morphism f there is a morphism g that is both left and right inverse to f under composition. A morphism that is invertible in this sense is called an isomorphism.
A
Any
The class of all preordered sets with order-preserving functions (i.e., monotone-increasing functions) as morphisms forms a category, Ord. It is a concrete category, i.e. a category obtained by adding some type of structure onto Set, and requiring that morphisms are functions that respect this added structure.
The class of all groups with
The class of all graphs forms another concrete category, where morphisms are graph homomorphisms (i.e., mappings between graphs which send vertices to vertices and edges to edges in a way that preserves all adjacency and incidence relations).
Other examples of concrete categories are given by the following table.
| Category | Objects | Morphisms |
|---|---|---|
| Set | sets | functions |
| Ord | preordered sets | monotone-increasing functions |
Mon
|
monoids
|
monoid homomorphisms |
| Grp | groups | group homomorphisms |
| Grph | graphs | graph homomorphisms |
| Ring | rings | ring homomorphisms |
Field
|
fields | field homomorphisms
|
| R-Mod | R-modules, where R is a ring | R-module homomorphisms |
VectK
|
vector spaces over the field K | K-linear maps |
| Met | metric spaces | short maps
|
| Meas | measure spaces | measurable functions |
| Top | topological spaces | continuous functions
|
| Manp | smooth manifolds
|
p-times continuously differentiable maps
|
Fiber bundles with bundle maps between them form a concrete category.
The category Cat consists of all small categories, with functors between them as morphisms.
Construction of new categories
Dual category
Any category C can itself be considered as a new category in a different way: the objects are the same as those in the original category but the arrows are those of the original category reversed. This is called the dual or opposite category and is denoted Cop.
Product categories
If C and D are categories, one can form the product category C × D: the objects are pairs consisting of one object from C and one from D, and the morphisms are also pairs, consisting of one morphism in C and one in D. Such pairs can be composed
Types of morphisms
A morphism f : a → b is called
- a monomorphism (or monic) if it is left-cancellable, i.e. fg1 = fg2 implies g1 = g2 for all morphisms g1, g2 : x → a.
- an epimorphism (or epic) if it is right-cancellable, i.e. g1f = g2f implies g1 = g2 for all morphisms g1, g2 : b → x.
- a bimorphismif it is both a monomorphism and an epimorphism.
- a retractionif it has a right inverse, i.e. if there exists a morphism g : b → a with fg = 1b.
- a section if it has a left inverse, i.e. if there exists a morphism g : b → a with gf = 1a.
- an isomorphism if it has an inverse, i.e. if there exists a morphism g : b → a with fg = 1b and gf = 1a.
- an endomorphism if a = b. The class of endomorphisms of a is denoted end(a). For locally small categories, end(a) is a set and forms a monoid under morphism composition.
- an automorphism if f is both an endomorphism and an isomorphism. The class of automorphisms of a is denoted aut(a). For locally small categories, it forms a group under morphism composition called the automorphism group of a.
Every retraction is an epimorphism. Every section is a monomorphism. The following three statements are equivalent:
- f is a monomorphism and a retraction;
- f is an epimorphism and a section;
- f is an isomorphism.
Relations among morphisms (such as fg = h) can most conveniently be represented with commutative diagrams, where the objects are represented as points and the morphisms as arrows.
Types of categories
- In many categories, e.g. VectK, the hom-sets hom(a, b) are not just sets but actually abelian groups, and the composition of morphisms is compatible with these group structures; i.e. is bilinear. Such a category is called preadditive. If, furthermore, the category has all finite products and coproducts, it is called an additive category. If all morphisms have a kernel and a cokernel, and all epimorphisms are cokernels and all monomorphisms are kernels, then we speak of an abelian category. A typical example of an abelian category is the category of abelian groups.
- A category is called complete if all small limits exist in it. The categories of sets, abelian groups and topological spaces are complete.
- A category is called cartesian closed if it has finite direct products and a morphism defined on a finite product can always be represented by a morphism defined on just one of the factors. Examples include Set and CPO, the category of complete partial orders with Scott-continuous functions.
- A topos is a certain type of cartesian closed category in which all of mathematics can be formulated (just like classically all of mathematics is formulated in the category of sets). A topos can also be used to represent a logical theory.
See also
- Enriched category
- Higher category theory
- Quantaloid
- Table of mathematical symbols
Notes
- ^ Barr & Wells 2005, Chapter 1
- ^ Some authors write Mor(a, b) or simply C(a, b) instead.
References
- Adámek, Jiří; Herrlich, Horst; Strecker, George E. (1990), Abstract and Concrete Categories (PDF), Wiley, ISBN 0-471-60922-6 (now free on-line edition, GNU FDL).
- Asperti, Andrea; Longo, Giuseppe (1991), Categories, Types and Structures, MIT Press, ISBN 0-262-01125-5.
- Awodey, Steve (2006), Category theory, Oxford logic guides, vol. 49, Oxford University Press, ISBN 978-0-19-856861-2.
- MR 2178101.
- Borceux, Francis (1994), "Handbook of Categorical Algebra", Encyclopedia of Mathematics and its Applications, vol. 50–52, Cambridge: Cambridge University Press, ISBN 0-521-06119-9.
- "Category", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Herrlich, Horst; Strecker, George E. (2007), Category Theory, Heldermann Verlag, ISBN 978-3-88538-001-6.
- ISBN 978-0-486-47187-7.
- ISBN 0-521-47249-0.
- ISBN 0-387-98403-8.
- Marquis, Jean-Pierre (2006), "Category Theory", in Zalta, Edward N. (ed.), Stanford Encyclopedia of Philosophy.
- Sica, Giandomenico (2006), What is category theory?, Advanced studies in mathematics and logic, vol. 3, Polimetrica, ISBN 978-88-7699-031-1.
- category at the nLab



